Hostname: page-component-5b777bbd6c-ks5gx Total loading time: 0 Render date: 2025-06-20T21:40:00.888Z Has data issue: false hasContentIssue false
  • English
  • Français

Sojourn functionals of time-dependent 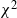$\chi^2$-random fields on two-point homogeneous spaces

Part of: Geometric probability and stochastic geometry Limit theorems Stochastic processes

Published online by Cambridge University Press:  13 June 2025

Alessia Caponera ,
Maurizia Rossi  and
María Dolores Ruiz Medina
Alessia Caponera*
Affiliation:
LUISS Guido Carli
Maurizia Rossi*
Affiliation:
Università di Milano-Bicocca
María Dolores Ruiz Medina*
Affiliation:
Universidad de Granada
*
*Email address: acaponera@luiss.it
**Email address: maurizia.rossi@unimib.it
***Email address: mruiz@ugr.es
Get access Rights & Permissions [Opens in a new window]

Abstract

We investigate geometric properties of invariant spatio-temporal random fields $X\colon\mathbb M^d\times \mathbb R\to \mathbb R$ defined on a compact two-point homogeneous space 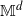$\mathbb M^d$ in any dimension 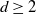$d\ge 2$, and evolving over time. In particular, we focus on chi-squared-distributed random fields, and study the large-time behavior (as 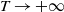$T\to +\infty$) of the average on [0,T] of the volume of the excursion set on the manifold, i.e. of 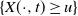$\lbrace X(\cdot, t)\ge u\rbrace$ (for any 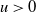$u >0$). The Fourier components of X may have short or long memory in time, i.e. integrable or non-integrable temporal covariance functions. Our argument follows the approach developed in Marinucci et al. (2021) and allows us to extend their results for invariant spatio-temporal Gaussian fields on the two-dimensional unit sphere to the case of chi-squared distributed fields on two-point homogeneous spaces in any dimension. We find that both the asymptotic variance and limiting distribution, as $T\to +\infty$, of the average empirical volume turn out to be non-universal, depending on the memory parameters of the field X.

Keywords

Chi-square random fieldscentral and non-central limit theoremsWiener chaostwo-point homogeneous spaces

MSC classification

Primary: 60G60: Random fields
Secondary: 60F05: Central limit and other weak theorems 60D05: Geometric probability and stochastic geometry 33C45: Orthogonal polynomials and functions of hypergeometric type (Jacobi, Laguerre, Hermite, Askey scheme, etc.)
Type
Original Article
Information
Journal of Applied Probability , First View , pp. 1 - 20
Check for updates
Copyright
© The Author(s), 2025. Published by Cambridge University Press on behalf of Applied Probability Trust

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Article purchase

Temporarily unavailable

References

Abramowitz, M. and Stegun, I. A. (1964). Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables (National Bureau of Standards Appl. Math. Ser. 55). U.S. Government Printing Office, Washington, DC.Google Scholar
Caponera, A., Marinucci, D. and Vidotto, A. (2023). Multiscale CUSUM tests for time-dependent spherical random fields. Preprint, arXiv:2305.01392.Google Scholar
Carones, A., Carrón Duque, J., Marinucci, D., Migliaccio, M. and Vittorio, N. (2023). Minkowski functionals of CMB polarization intensity with pynkowski: Theory and application to Planck and future data. Mon. Not. R. Astron. Soc. 527, 756–773.10.1093/mnras/stad3002CrossRefGoogle Scholar
Dębicki, K., Hashorva, E., Liu, P. and Michna, Z. (2023). Sojourn times of Gaussian and related random fields. ALEA Lat. Am. J. Prob. Math. Stat. 20, 249–289.10.30757/ALEA.v20-10CrossRefGoogle Scholar
Dobrushin, R. L. and Major, P. (1979). Non-central limit theorems for nonlinear functionals of Gaussian fields. Z. Wahrscheinlichkeitsth. 50, 27–52.10.1007/BF00535673CrossRefGoogle Scholar
Giné Masdéu, E. (1975). The addition formula for the eigenfunctions of the Laplacian. Adv. Math. 18, 102–107.Google Scholar
Helgason, S. (1959). Differential operators on homogeneous spaces. Acta Math. 102, 239–299.CrossRefGoogle Scholar
Hille, E. (1926). A class of reciprocal functions. Ann. Math. 27, 427–464.10.2307/1967695CrossRefGoogle Scholar
Köhler-Schindler, L. and Tassion, V. (2023). Crossing probabilities for planar percolation. Duke Math. J. 172, 809–838.10.1215/00127094-2022-0015CrossRefGoogle Scholar
Kushpel, A. (2021). The Lebesgue constants on projective spaces. Turkish J. Math. 45, 856–863.CrossRefGoogle Scholar
Kushpel, A. and Tozoni, S. A. (2012). Entropy and widths of multiplier operators on two-point homogeneous spaces. Constr. Approx. 35, 137–180.10.1007/s00365-011-9146-7CrossRefGoogle Scholar
Leonenko, N., Maini, L., Nourdin, I. and Pistolato, F. (2024). Limit theorems for p-domain functionals of stationary Gaussian fields. Electron. J. Prob. 29, 1–33.CrossRefGoogle Scholar
Leonenko, N. and Olenko, A. (2014). Sojourn measures of Student and Fisher–Snedecor random fields. Bernoulli 20, 1454–1483.10.3150/13-BEJ529CrossRefGoogle Scholar
Leonenko, N. N. and Ruiz-Medina, M. D. (2023). Sojourn functionals for spatiotemporal Gaussian random fields with long memory. J. Appl. Prob. 60, 148–165.10.1017/jpr.2022.30CrossRefGoogle Scholar
Leonenko, N. N., Ruiz-Medina, M. D. and Taqqu, M. S. (2017). Non-central limit theorems for random fields subordinated to Gamma-correlated random fields. Bernoulli 23, 3469–3507.CrossRefGoogle Scholar
Leonenko, N. N., Ruiz-Medina, M. D. and Taqqu, M. S. (2017). Rosenblatt distribution subordinated to Gaussian random fields with long-range dependence. Stoch. Anal. Appl. 35, 144–177.CrossRefGoogle Scholar
Leonenko, N. N., Taqqu, M. S. and Terdik, G. H. (2018). Estimation of the covariance function of Gaussian isotropic random fields on spheres, related Rosenblatt-type distributions and the cosmic variance problem. Electron. J. Statist. 12, 3114–3146.CrossRefGoogle Scholar
Lu, T., Ma, C. and Xiao, Y. (2023). Strong local nondeterminism and exact modulus of continuity for isotropic Gaussian random fields on compact two-point homogeneous spaces. J. Theoret. Prob. 36, 2403–2425.CrossRefGoogle Scholar
Ma, C. and Malyarenko, A. (2020). Time-varying isotropic vector random fields on compact two-point homogeneous spaces. J. Theoret. Prob. 33, 319–339.CrossRefGoogle Scholar
Makogin, V. and Spodarev, E. (2022). Limit theorems for excursion sets of subordinated Gaussian random fields with long-range dependence. Stochastics 94, 111–142.10.1080/17442508.2021.1914620CrossRefGoogle Scholar
Marinucci, D. and Peccati, G. (2011). Random Fields on the Sphere: Representation, Limit Theorems and Cosmological Applications. Cambridge University Press.10.1017/CBO9780511751677CrossRefGoogle Scholar
Marinucci, D., Peccati, G., Rossi, M. and Wigman, I. (2016). Non-universality of nodal length distribution for arithmetic random waves. Geom. Funct. Anal. 26, 926–960.CrossRefGoogle Scholar
Marinucci, D., Rossi, M. and Vidotto, A. (2021). Non-universal fluctuations of the empirical measure for isotropic stationary fields on $\Bbb S^2 \times \Bbb R$ . Ann. Appl. Prob. 31, 2311–2349.CrossRefGoogle Scholar
Marinucci, D., Rossi, M. and Vidotto, A. (2024). Fluctuations of level curves for time-dependent spherical random fields. Ann. H. Lebesgue 7, 583–620.10.5802/ahl.206CrossRefGoogle Scholar
Marinucci, D. and Stecconi, M. (2024). Critical points of chi-fields. Preprint, arXiv:2409.20129.Google Scholar
Nourdin, I. and Peccati, G. (2012). Normal Approximations with Malliavin Calculus: From Stein’s Method to Universality (Camb. Tracts Math. 192). Cambridge University Press.CrossRefGoogle Scholar
Peccati, G. and Taqqu, M. S. (2011). Wiener Chaos: Moments, Cumulants and Diagrams. Springer, Milan.CrossRefGoogle Scholar
Sun, Y. and Baricz, A. (2008). Inequalities for the generalized Marcum Q-function. Appl. Math. Comput. 203, 134–141.Google Scholar
Szegö, G. (1967). Orthogonal Polynomials, 3rd edn (Amer. Math. Soc. Colloq. Pub. 23). American Mathematical Society, Providence, RI.Google Scholar
Taqqu, M. S. (1975). Weak convergence to fractional Brownian motion and to the Rosenblatt process. Z. Wahrscheinlichkeitsth. 31, 287–302.CrossRefGoogle Scholar
Taqqu, M. S. (1979). Convergence of integrated processes of arbitrary Hermite rank. Z. Wahrscheinlichkeitsth. 50, 53–83.10.1007/BF00535674CrossRefGoogle Scholar
Wang, H.-C. (1952). Two-point homogeneous spaces. Ann. Math. 55, 177–191.CrossRefGoogle Scholar