Article contents
Sojourn functionals for spatiotemporal Gaussian random fields with long memory
Published online by Cambridge University Press: 09 February 2023
Abstract
This paper addresses the asymptotic analysis of sojourn functionals of spatiotemporal Gaussian random fields with long-range dependence (LRD) in time, also known as long memory. Specifically, reduction theorems are derived for local functionals of nonlinear transformation of such fields, with Hermite rank 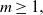 $m\geq 1,$ under general covariance structures. These results are proven to hold, in particular, for a family of nonseparable covariance structures belonging to the Gneiting class. For
$m\geq 1,$ under general covariance structures. These results are proven to hold, in particular, for a family of nonseparable covariance structures belonging to the Gneiting class. For 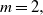 $m=2,$ under separability of the spatiotemporal covariance function in space and time, the properly normalized Minkowski functional, involving the modulus of a Gaussian random field, converges in distribution to the Rosenblatt-type limiting distribution for a suitable range of values of the long-memory parameter.
$m=2,$ under separability of the spatiotemporal covariance function in space and time, the properly normalized Minkowski functional, involving the modulus of a Gaussian random field, converges in distribution to the Rosenblatt-type limiting distribution for a suitable range of values of the long-memory parameter.
Keywords
MSC classification
Information
- Type
- Original Article
- Information
- Copyright
- © The Author(s), 2023. Published by Cambridge University Press on behalf of Applied Probability Trust
References
- 6
- Cited by


