Article contents
Renewal theory for iterated perturbed random walks on a general branching process tree: Early generations
Published online by Cambridge University Press: 02 September 2022
Abstract
Let 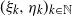 $(\xi_k,\eta_k)_{k\in\mathbb{N}}$ be independent identically distributed random vectors with arbitrarily dependent positive components. We call a (globally) perturbed random walk a random sequence
$(\xi_k,\eta_k)_{k\in\mathbb{N}}$ be independent identically distributed random vectors with arbitrarily dependent positive components. We call a (globally) perturbed random walk a random sequence 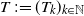 $T\,{:\!=}\, (T_k)_{k\in\mathbb{N}}$ defined by
$T\,{:\!=}\, (T_k)_{k\in\mathbb{N}}$ defined by 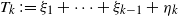 $T_k\,{:\!=}\, \xi_1+\cdots+\xi_{k-1}+\eta_k$ for
$T_k\,{:\!=}\, \xi_1+\cdots+\xi_{k-1}+\eta_k$ for 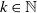 $k\in\mathbb{N}$. Consider a general branching process generated by T and let
$k\in\mathbb{N}$. Consider a general branching process generated by T and let 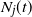 $N_j(t)$ denote the number of the jth generation individuals with birth times
$N_j(t)$ denote the number of the jth generation individuals with birth times 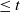 $\leq t$. We treat early generations, that is, fixed generations j which do not depend on t. In this setting we prove counterparts for
$\leq t$. We treat early generations, that is, fixed generations j which do not depend on t. In this setting we prove counterparts for 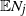 $\mathbb{E}N_j$ of the Blackwell theorem and the key renewal theorem, prove a strong law of large numbers for
$\mathbb{E}N_j$ of the Blackwell theorem and the key renewal theorem, prove a strong law of large numbers for 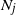 $N_j$, and find the first-order asymptotics for the variance of
$N_j$, and find the first-order asymptotics for the variance of 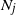 $N_j$. Also, we prove a functional limit theorem for the vector-valued process
$N_j$. Also, we prove a functional limit theorem for the vector-valued process 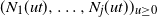 $(N_1(ut),\ldots, N_j(ut))_{u\geq0}$, properly normalized and centered, as
$(N_1(ut),\ldots, N_j(ut))_{u\geq0}$, properly normalized and centered, as 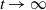 $t\to\infty$. The limit is a vector-valued Gaussian process whose components are integrated Brownian motions.
$t\to\infty$. The limit is a vector-valued Gaussian process whose components are integrated Brownian motions.
Keywords
MSC classification
Information
- Type
- Original Article
- Information
- Copyright
- © The Author(s), 2022. Published by Cambridge University Press on behalf of Applied Probability Trust
References
- 4
- Cited by


