Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Smith, M.A.J.
Aven, T.
Dekker, R.
and
Van der Duyn Schouten, F.A.
1997.
Advances in Safety and Reliability.
p.
1727.
Bon, Jean-Louis
and
Bretagnolle, Jean
1998.
Evaluation a priori de la probabilité de défaillance d'un système réparable.
Comptes Rendus de l'Académie des Sciences - Series I - Mathematics,
Vol. 326,
Issue. 6,
p.
743.
Bon, Jean-Louis
and
Bretagnolle, Jean
1999.
Approximation of Reliability for a large system with non-markovian repair-times.
ESAIM: Probability and Statistics,
Vol. 3,
Issue. ,
p.
49.
Collet, J.
and
Bon, J.L.
2002.
Bracketing of failure path probability in a system with ageing repair times.
Reliability Engineering & System Safety,
Vol. 76,
Issue. 2,
p.
139.
Lagos, Guido
Barrera, Javiera
Romero, Pablo
and
Valencia, Juan
2024.
Limiting Behavior of Mixed Coherent Systems With Lévy‐Frailty Marshall–Olkin Failure Times.
Applied Stochastic Models in Business and Industry,
Vol. 40,
Issue. 5,
p.
1229.

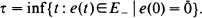 .
.