Article contents
Records for time-dependent stationary Gaussian sequences
Published online by Cambridge University Press: 04 May 2020
Abstract
For a zero-mean, unit-variance stationary univariate Gaussian process we derive the probability that a record at the time n, say 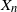 $X_n$, takes place, and derive its distribution function. We study the joint distribution of the arrival time process of records and the distribution of the increments between records. We compute the expected number of records. We also consider two consecutive and non-consecutive records, one at time j and one at time n, and we derive the probability that the joint records
$X_n$, takes place, and derive its distribution function. We study the joint distribution of the arrival time process of records and the distribution of the increments between records. We compute the expected number of records. We also consider two consecutive and non-consecutive records, one at time j and one at time n, and we derive the probability that the joint records 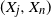 $(X_j,X_n)$ occur, as well as their distribution function. The probability that the records
$(X_j,X_n)$ occur, as well as their distribution function. The probability that the records 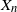 $X_n$ and
$X_n$ and 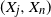 $(X_j,X_n)$ take place and the arrival time of the nth record are independent of the marginal distribution function, provided that it is continuous. These results actually hold for a strictly stationary process with Gaussian copulas.
$(X_j,X_n)$ take place and the arrival time of the nth record are independent of the marginal distribution function, provided that it is continuous. These results actually hold for a strictly stationary process with Gaussian copulas.
Keywords
MSC classification
Information
- Type
- Research Papers
- Information
- Copyright
- © Applied Probability Trust 2020
References
- 3
- Cited by

