Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Saint-Mont, Uwe
2003.
Comparison of Values of Independent Random Variables in a Bayesian Setting.
Sequential Analysis,
Vol. 22,
Issue. 1-2,
p.
159.
Agarwal, R.P.
Barnett, N.S.
Cerone, P.
and
Dragomir, S.S.
2005.
A survey on some inequalities for expectation and variance.
Computers & Mathematics with Applications,
Vol. 49,
Issue. 2-3,
p.
429.
Osȩkowski, Adam
2013.
A prophet inequality for L2-martingales.
Statistics & Probability Letters,
Vol. 83,
Issue. 10,
p.
2319.
Osȩkowski, Adam
2015.
A prophet inequality for $$L^p$$ L p -bounded dependent random variables.
Positivity,
Vol. 19,
Issue. 2,
p.
289.

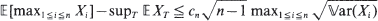 , where the supremum is over all stopping times
, where the supremum is over all stopping times 