Article contents
Oscillations for order statistics of some discrete processes
Published online by Cambridge University Press: 04 September 2020
Abstract
Suppose k balls are dropped into n boxes independently with uniform probability, where n, k are large with ratio approximately equal to some positive real 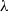 $\lambda$. The maximum box count has a counterintuitive behavior: first of all, with high probability it takes at most two values
$\lambda$. The maximum box count has a counterintuitive behavior: first of all, with high probability it takes at most two values 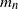 $m_n$ or
$m_n$ or 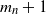 $m_n+1$, where
$m_n+1$, where 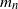 $m_n$ is roughly
$m_n$ is roughly 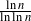 $\frac{\ln n}{\ln \ln n}$. Moreover, it oscillates between these two values with an unusual periodicity. In order to prove this statement and various generalizations, it is first shown that for
$\frac{\ln n}{\ln \ln n}$. Moreover, it oscillates between these two values with an unusual periodicity. In order to prove this statement and various generalizations, it is first shown that for 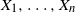 $X_1,\ldots,X_n$ independent and identically distributed discrete random variables with common distribution F, under mild conditions, the limiting distribution of their maximum oscillates in three possible families, depending on the tail of the distribution. The result stated at the beginning follows from the ensemble equivalence for the order statistics in various allocations problems, obtained via conditioning limit theory. Results about the number of ties for the maximum, as well as applications, are also provided.
$X_1,\ldots,X_n$ independent and identically distributed discrete random variables with common distribution F, under mild conditions, the limiting distribution of their maximum oscillates in three possible families, depending on the tail of the distribution. The result stated at the beginning follows from the ensemble equivalence for the order statistics in various allocations problems, obtained via conditioning limit theory. Results about the number of ties for the maximum, as well as applications, are also provided.
MSC classification
Information
- Type
- Research Papers
- Information
- Copyright
- © Applied Probability Trust 2020
References
- 1
- Cited by


