No CrossRef data available.
Article contents
Optimal stopping under g-Expectation with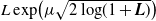 
${L}\exp\bigl(\mu\sqrt{2\log\!(1+\textbf{L})}\bigr)$-integrable reward process
Published online by Cambridge University Press: 14 September 2022
Abstract
In this paper we study a class of optimal stopping problems under g-expectation, that is, the cost function is described by the solution of backward stochastic differential equations (BSDEs). Primarily, we assume that the reward process is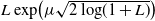 
$L\exp\bigl(\mu\sqrt{2\log\!(1+L)}\bigr)$-integrable with 
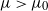$\mu>\mu_0$ for some critical value 
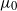$\mu_0$. This integrability is weaker than 
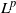$L^p$-integrability for any 
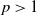$p>1$, so it covers a comparatively wide class of optimal stopping problems. To reach our goal, we introduce a class of reflected backward stochastic differential equations (RBSDEs) with 
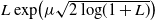$L\exp\bigl(\mu\sqrt{2\log\!(1+L)}\bigr)$-integrable parameters. We prove the existence, uniqueness, and comparison theorem for these RBSDEs under Lipschitz-type assumptions on the coefficients. This allows us to characterize the value function of our optimal stopping problem as the unique solution of such RBSDEs.
Keywords
Information
- Type
- Original Article
- Information
- Copyright
- © The Author(s), 2022. Published by Cambridge University Press on behalf of Applied Probability Trust
References
Bayraktar, E. and Yao, S. (2011). Optimal stopping for non-linear expectations, II. Stoch. Process. Appl. 121, 212–264.CrossRefGoogle Scholar
Bayraktar, E. and Yao, S. (2012). Quadratic reflected BSDEs with unbounded obstacles. Stoch. Process. Appl. 122, 1155–1203.CrossRefGoogle Scholar
Bayraktar, E., Karatzas, I. and Yao, S. (2010). Optimal stopping for dynamic convex risk measures. Illinois J. Math. 54, 1025–1067.CrossRefGoogle Scholar
Buckdahn, R., Hu, Y. and Tang, S. (2018). Uniqueness of solution to scalar BSDEs with
$L\exp\bigl(\mu\sqrt{2\log\!(1+L)}\bigr)$
-integrable terminal values. Electron. Commun. Prob. 23, 59.Google Scholar
$L\exp\bigl(\mu\sqrt{2\log\!(1+L)}\bigr)$
-integrable terminal values. Electron. Commun. Prob. 23, 59.Google ScholarChen, Z. and Epstein, L. (2002). Ambiguity, risk and asset returns in continuous time. Econometrica 70, 1403–1443.CrossRefGoogle Scholar
Delbaen, F., Peng, S. and Rosazza Gianin, E. (2010). Representation of the penalty term of dynamic concave utilities. Finance Stoch. 14, 449–472.CrossRefGoogle Scholar
Duffie, D. and Epstein, L. (1992). Stochastic differential utility. Econometrica 60, 353–394.CrossRefGoogle Scholar
El Karoui, N. (1981). Les aspects probabilistes du contrôle stochastique. In Ninth Saint Flour Probability Summer School 1979 (Lecture Notes Math. 876), pp. 73–238. Springer, Berlin.Google Scholar
El Karoui, N., Kapoudjian, C., Pardoux, E., Peng, S. and Quenez, M.C. (1997). Reflected solutions of backward SDE’s and related obstacle problems for PDE’s. Ann. Prob. 25, 702–737.CrossRefGoogle Scholar
El Karoui, N., Pardoux, E. and Quenez, M. C. (1997). Reflected backward SDEs and American options. In Numerical Methods in Finance, eds L. C. G. Rogers and D. Talay, pp. 215–231. Cambridge University Press.CrossRefGoogle Scholar
Fan, S. and Hu, Y. (2019). Existence and uniqueness of solution to scalar BSDEs with
$L\exp\bigl(\mu\sqrt{2\log\!(1+L)}\bigr)$
-integrable terminal values: the critical case. Electron. Commun. Prob. 24, 49.CrossRefGoogle Scholar
$L\exp\bigl(\mu\sqrt{2\log\!(1+L)}\bigr)$
-integrable terminal values: the critical case. Electron. Commun. Prob. 24, 49.CrossRefGoogle ScholarHamadène, S. and Popier, A. (2012).
$L^p$
-solutions for reflected backward stochastic differential equations. Stoch. Dyn. 12, 1150016.CrossRefGoogle Scholar
$L^p$
-solutions for reflected backward stochastic differential equations. Stoch. Dyn. 12, 1150016.CrossRefGoogle ScholarHu, Y. and Tang, S. (2018). Existence of solution to scalar BSDEs with
$L\exp\bigl(\sqrt{\frac{2}{\lambda}\log(1+L)}\bigr)$
-integrable terminal values. Electron. Commun. Prob. 23, 27.Google Scholar
$L\exp\bigl(\sqrt{\frac{2}{\lambda}\log(1+L)}\bigr)$
-integrable terminal values. Electron. Commun. Prob. 23, 27.Google ScholarKlenke, A. (2008). Probability Theory: A Comprehensive Course (Universitext). Springer, London.CrossRefGoogle Scholar
Klimsiak, T. (2012). Reflected BSDEs with monotone generator. Electron. J. Prob. 17, 107.CrossRefGoogle Scholar
Kobylanski, M., Lepeltier, J. P., Quenez, M. C. and Torres, S. (2002) Reflected BSDEs with superlinear quadratic coefficient. Prob. Math. Statist. 22, 51–83.Google Scholar
Lepeltier, J. P. and Xu, M. (2007). Reflected BSDE with quadratic growth and unbounded terminal value. Available at arXiv:0711.0619.Google Scholar
Lepeltier, J. P., Matoussi, A. and Xu, M. (2005). Reflected backward stochastic differential equations under monotonicity and general increasing growth conditions. Adv. Appl. Prob. 37, 134–159.CrossRefGoogle Scholar
Peng, S. (1997). Backward SDE and related g-expectation. In Backward Stochastic Differential Equations (Pitman Res. Notes Math. Ser. 364), eds N. El Karoui and L. Mazliak, pp. 141–159. Longman, Harlow.Google Scholar
Quenez, M.C. and Sulem, A. (2014). Reflected BSDEs and robust optimal stopping for dynamic risk measures with jumps. Stoch. Process. Appl. 124, 3031–3054.CrossRefGoogle Scholar
Rosazza Gianin, E. (2006). Risk measures via g-expectations. Insurance Math. Econom. 39, 19–34.CrossRefGoogle Scholar
Rozkosz, A. and Slomiński, L. (2012).
$L^p$
-solutions of reflected BSDEs under monotonicity condition. Stoch. Process. Appl. 122, 3875–3900.CrossRefGoogle Scholar
$L^p$
-solutions of reflected BSDEs under monotonicity condition. Stoch. Process. Appl. 122, 3875–3900.CrossRefGoogle ScholarWu, H. (2013). Optimal stopping under g-expectation with constraints. Operat. Res. Lett. 41, 164–171.CrossRefGoogle Scholar