Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Attia, F.A.
1989.
A note on the expected discounted cost of operating a finite dam.
Stochastic Processes and their Applications,
Vol. 31,
Issue. 1,
p.
161.
Attia, F. A.
1989.
Resolvent operators of Markov processes and their applications in the control of a finite dam.
Journal of Applied Probability,
Vol. 26,
Issue. 02,
p.
314.
Abdel-hameed, M.
and
Nakhi, Y.
1990.
Optimal control of a finite dam using P
M
λΤ policies and penalty cost: total discounted and long run average cases.
Journal of Applied Probability,
Vol. 27,
Issue. 04,
p.
888.
Dohi, T.
Kaio, N.
and
Osaki, S.
1993.
Continuous time inventory control for wiener process demand.
Computers & Mathematics with Applications,
Vol. 26,
Issue. 9,
p.
11.
Fox, David
Zarmi, Yair
and
Zemel, Amos
1994.
Stochastic and Statistical Methods in Hydrology and Environmental Engineering.
Vol. 10/4,
Issue. ,
p.
255.
Abdel‐Hameed, Mohamed
and
Nakhi, Yasmin
1995.
Optimal control of dams.
Applied Stochastic Models and Data Analysis,
Vol. 11,
Issue. 1,
p.
25.
Abdel-Hameed, M.
2003.
Optimal control of dams using Pλ,τM policies and penalty cost.
Mathematical and Computer Modelling,
Vol. 38,
Issue. 11-13,
p.
1119.
Miller, Boris
and
McInnes, Daniel
2011.
Optimal management of a two dam system via stochastic control: Parallel computing approach.
p.
1417.
Abdel-Hameed, Mohamed
2011.
Control of Dams Using Pλ,τM Policies When the Input Process Is a Nonnegative Lévy Process.
International Journal of Stochastic Analysis,
Vol. 2011,
Issue. ,
p.
1.
Miller, Boris M.
and
McInnes, Daniel J.
2011.
Management of a Large Dam via Optimal Price Control.
IFAC Proceedings Volumes,
Vol. 44,
Issue. 1,
p.
12432.
Miller, Boris M.
and
McInnes, Daniel J.
2011.
Management of dam systems via optimal price control.
Procedia Computer Science,
Vol. 4,
Issue. ,
p.
1373.
McInnes, Daniel
and
Miller, Boris
2013.
Optimal control of time-inhomogeneous Markov chains with application to dam management.
p.
230.
Lust, A.
and
Waldmann, K.-H.
2019.
A general storage model with applications to energy systems.
OR Spectrum,
Vol. 41,
Issue. 1,
p.
71.
Chevalier, Etienne
Di Girolami, Cristina
Gaïgi, M'hamed
Giovannini, Elisa
and
Scotti, Simone
2024.
A dam management problem with energy production as an optimal switching problem.
Applied Stochastic Models in Business and Industry,
Vol. 40,
Issue. 6,
p.
1596.

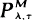 has been considered by Lam Yeh [6], [7]. In this paper, by using the first Dynkin formula, the same problems of specifying an optimal policy in the class of the policies
has been considered by Lam Yeh [6], [7]. In this paper, by using the first Dynkin formula, the same problems of specifying an optimal policy in the class of the policies 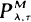 to minimize the expected total discounted cost as well as the long-run average cost are considered. Both the expected total discounted cost and long-run average cost are determined explicitly, and then the optimal policy can be found numerically, Also, we obtain the transition density function and the resolvent operator of a reflecting Wiener process.
to minimize the expected total discounted cost as well as the long-run average cost are considered. Both the expected total discounted cost and long-run average cost are determined explicitly, and then the optimal policy can be found numerically, Also, we obtain the transition density function and the resolvent operator of a reflecting Wiener process.