Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Attia, F.A.
1989.
A note on the expected discounted cost of operating a finite dam.
Stochastic Processes and their Applications,
Vol. 31,
Issue. 1,
p.
161.
Attia, F. A.
1989.
Resolvent operators of Markov processes and their applications in the control of a finite dam.
Journal of Applied Probability,
Vol. 26,
Issue. 02,
p.
314.
Bulinskaya, E.V.
1989.
Functional limit theorems for some inventory models.
Engineering Costs and Production Economics,
Vol. 15,
Issue. ,
p.
323.
Attia, F.A.
1991.
On a reflected Ornstein-Uhlenbeck process with an application.
Bulletin of the Australian Mathematical Society,
Vol. 43,
Issue. 3,
p.
519.
Dohi, T.
Kaio, N.
and
Osaki, S.
1993.
Continuous time inventory control for wiener process demand.
Computers & Mathematics with Applications,
Vol. 26,
Issue. 9,
p.
11.
Lim, Kyung Eun
Baek, Jee Seon
and
Lee, Eui Yong
2005.
Optimization under the PMλ,τ policy of a finite dam with both continuous and jumpwise inputs.
Journal of Applied Probability,
Vol. 42,
Issue. 2,
p.
587.
Lim, Kyung Eun
Baek, Jee Seon
and
Lee, Eui Yong
2005.
Optimization under the P
M
λ,τ policy of a finite dam with both continuous and jumpwise inputs.
Journal of Applied Probability,
Vol. 42,
Issue. 02,
p.
587.
Lee, Jiyeon
and
Kim, Jongwoo
2006.
A workload-dependent queue under a two-stage service policy.
Operations Research Letters,
Vol. 34,
Issue. 5,
p.
531.
Bekker, R.
2009.
Queues with Lévy input and hysteretic control.
Queueing Systems,
Vol. 63,
Issue. 1-4,
p.
281.
Kim, Jongwoo
Song, Mi Jung
and
Lee, Jiyeon
2013.
A two-stage service policy for an M/G/1 queueing system.
Journal of the Korean Data and Information Science Society,
Vol. 24,
Issue. 4,
p.
941.
Boxma, O.
Löpker, A.
and
Perry, D.
2016.
On a make-to-stock production/mountain modeln with hysteretic control.
Annals of Operations Research,
Vol. 241,
Issue. 1-2,
p.
53.
Kim, Sunggon
2018.
Conditional sojourn time distributions in M/G/1 and G/M/1 queues under PλM-service policy.
Communications for Statistical Applications and Methods,
Vol. 25,
Issue. 4,
p.
443.
Jonsson, Adam
2024.
On singular control of reflected diffusions.
Electronic Communications in Probability,
Vol. 29,
Issue. none,
Chevalier, Etienne
Di Girolami, Cristina
Gaïgi, M'hamed
Giovannini, Elisa
and
Scotti, Simone
2024.
A dam management problem with energy production as an optimal switching problem.
Applied Stochastic Models in Business and Industry,
Vol. 40,
Issue. 6,
p.
1596.
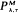 of the following type. Assume that the dam is initially empty, the release rate is kept at 0 until the dam storage increases to λ, and as soon as this occurs, water is released at rate M, then the output rate is kept at M as long as the dam storage is more than τ and it must be decreased to 0 if the dam storage becomes τ. We assume that the input of water into the finite dam is a Wiener process with non-negative drift μ and variance parameter σ2. There is a cost in increasing the output rate from 0 to M as well as in decreasing the rate from M to 0 and whenever the dam storage is below level a, there is a penalty cost per unit time depending on the level. A reward is given for each unit of water released. In this paper, the long-run average cost per unit time is determined, and therefore the optimal policy
of the following type. Assume that the dam is initially empty, the release rate is kept at 0 until the dam storage increases to λ, and as soon as this occurs, water is released at rate M, then the output rate is kept at M as long as the dam storage is more than τ and it must be decreased to 0 if the dam storage becomes τ. We assume that the input of water into the finite dam is a Wiener process with non-negative drift μ and variance parameter σ2. There is a cost in increasing the output rate from 0 to M as well as in decreasing the rate from M to 0 and whenever the dam storage is below level a, there is a penalty cost per unit time depending on the level. A reward is given for each unit of water released. In this paper, the long-run average cost per unit time is determined, and therefore the optimal policy 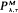 can be found numerically.
can be found numerically.
