No CrossRef data available.
Article contents
On some properties of distributions possessing a bathtub-shaped failure rate average
Published online by Cambridge University Press: 04 January 2023
Abstract
The life distribution of a device subject to shocks governed by a homogeneous Poisson process is shown to have a bathtub failure rate average (BFRA) when the probabilities 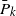 $\bar{P}_k$ of surviving k shocks possess the corresponding discrete property. We prove closure under the formation of weak limits for BFRA distributions and explore related moment convergence issues within the BFRA family. Similar results for increasing and decreasing failure rate average distributions are obtained either independently or as consequences of our results. We also establish some results outlining the positions of various non-monotonic ageing classes such as bathtub failure rate, increasing initially then decreasing mean residual life, new worse then better than used in expectation, and increasing initially then decreasing mean time to failure in the hierarchy. Finally, an open problem is posed and a partial solution provided.
$\bar{P}_k$ of surviving k shocks possess the corresponding discrete property. We prove closure under the formation of weak limits for BFRA distributions and explore related moment convergence issues within the BFRA family. Similar results for increasing and decreasing failure rate average distributions are obtained either independently or as consequences of our results. We also establish some results outlining the positions of various non-monotonic ageing classes such as bathtub failure rate, increasing initially then decreasing mean residual life, new worse then better than used in expectation, and increasing initially then decreasing mean time to failure in the hierarchy. Finally, an open problem is posed and a partial solution provided.
Keywords
MSC classification
Information
- Type
- Original Article
- Information
- Copyright
- © The Author(s), 2023. Published by Cambridge University Press on behalf of Applied Probability Trust


