Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Berg, Sven
and
Mutafchiev, Ljuben
1990.
Random mappings with an attracting center: Lagrangian distributions and a regression function.
Journal of Applied Probability,
Vol. 27,
Issue. 03,
p.
622.
Berg, Sven
and
Nowicki, Krzysztof
1991.
Statistical inference for a class of modified power series distributions with applications to random mapping theory.
Journal of Statistical Planning and Inference,
Vol. 28,
Issue. 2,
p.
247.
Sung, Yü
1994.
Ein einfaches Graphenmodell.
Mathematische Semesterberichte,
Vol. 41,
Issue. 2,
p.
157.
Aldous, David
and
Pitman, Jim
2002.
Asymptotic Combinatorics with Application to Mathematical Physics.
p.
113.
Hansen, Jennie C.
and
Jaworski, Jerzy
2009.
A random mapping with preferential attachment.
Random Structures & Algorithms,
Vol. 34,
Issue. 1,
p.
87.

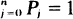 . A realization of
. A realization of 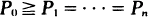 we observe the asymptotics of this distribution, as
we observe the asymptotics of this distribution, as 