Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
de Haan, L.
and
Resnick, S.
1987.
On regular variation of probability densities.
Stochastic Processes and their Applications,
Vol. 25,
Issue. ,
p.
83.
Brozius, Henk
1989.
Convergence in mean of some characteristics of the convex hull.
Advances in Applied Probability,
Vol. 21,
Issue. 3,
p.
526.
Aldous, David J.
Fristedt, Bert
Griffin, Philip S.
and
Pruitt, William E.
1991.
The number of extreme points in the convex hull of a random sample.
Journal of Applied Probability,
Vol. 28,
Issue. 02,
p.
287.
Glendinning, R.H.
1991.
The convex hull of a dependent vector-valued process.
Journal of Statistical Computation and Simulation,
Vol. 38,
Issue. 1-4,
p.
219.
Balkema, A. A.
De Haan, L.
and
Karandikar, R. L.
1993.
Asymptotic distribution of the maximum of n independent stochastic processes.
Journal of Applied Probability,
Vol. 30,
Issue. 01,
p.
66.
Massé, Bruno
1995.
Invariance principle for the deviation between the probability content and the interior point proportion of a random convex hull.
Journal of Applied Probability,
Vol. 32,
Issue. 04,
p.
1041.
Molchanov, I.S.
and
Stoyan, D.
1996.
Statistical models of random polyhedra∗.
Communications in Statistics. Stochastic Models,
Vol. 12,
Issue. 2,
p.
199.
Molchanov, I. S.
1996.
On the Convergence of Random Processes Generated by Polyhedral Approximation of Convex Compacts.
Theory of Probability & Its Applications,
Vol. 40,
Issue. 2,
p.
383.
Majumdar, Satya N.
Comtet, Alain
and
Randon-Furling, Julien
2010.
Random Convex Hulls and Extreme Value Statistics.
Journal of Statistical Physics,
Vol. 138,
Issue. 6,
p.
955.
Falk, Michael
Hüsler, Jürg
and
Reiss, Rolf-Dieter
2011.
Laws of Small Numbers: Extremes and Rare Events.
p.
311.
Weller, Grant B.
and
Eddy, William F.
2015.
Multivariate Order Statistics: Theory and Application.
Annual Review of Statistics and Its Application,
Vol. 2,
Issue. 1,
p.
237.
Molchanov, Ilya
2017.
Theory of Random Sets.
Vol. 87,
Issue. ,
p.
1.
Molchanov, Ilya
2017.
Theory of Random Sets.
Vol. 87,
Issue. ,
p.
225.
Simpson, Emma S.
and
Tawn, Jonathan A.
2024.
Inference for New Environmental Contours Using Extreme Value Analysis.
Journal of Agricultural, Biological and Environmental Statistics,
Simpson, Emma S.
and
Tawn, Jonathan A.
2024.
Estimating the limiting shape of bivariate scaled sample clouds: With additional benefits of self-consistent inference for existing extremal dependence properties.
Electronic Journal of Statistics,
Vol. 18,
Issue. 2,

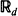 is studied using the support function. Results like that of Eddy and Gale (1981) are proved without the condition of spherical symmetry from that paper.
is studied using the support function. Results like that of Eddy and Gale (1981) are proved without the condition of spherical symmetry from that paper.