Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Durham, S. D.
1974.
Limiting distributions for the general branching process with immigration.
Journal of Applied Probability,
Vol. 11,
Issue. 4,
p.
809.
Durham, S. D.
1974.
Limiting distributions for the general branching process with immigration.
Journal of Applied Probability,
Vol. 11,
Issue. 04,
p.
809.
Bingham, N. H.
and
Doney, R. A.
1974.
Asymptotic properties of supercritical branching processes I: The Galton-Watson process.
Advances in Applied Probability,
Vol. 6,
Issue. 4,
p.
711.
Bingham, N. H.
and
Doney, R. A.
1975.
Asymptotic properties of super-critical branching processes II: Crump-Mode and Jirina processes.
Advances in Applied Probability,
Vol. 7,
Issue. 1,
p.
66.
Bingham, N.H.
1976.
Continuous branching processes and spectral positivity.
Stochastic Processes and their Applications,
Vol. 4,
Issue. 3,
p.
217.
Biggins, J. D.
1977.
Martingale convergence in the branching random walk.
Journal of Applied Probability,
Vol. 14,
Issue. 01,
p.
25.
Vatutin, V. A.
and
Zubkov, A. M.
1987.
Branching processes. I.
Journal of Soviet Mathematics,
Vol. 39,
Issue. 1,
p.
2431.
Liu, Quansheng
1996.
Trees.
p.
51.
Liu, Quansheng
1997.
Sur Une Équation Fonctionnelle Et SES Applications: Une Extension Du Théorème De Kesten-Stigum Concernant Des Processus De Branchement.
Advances in Applied Probability,
Vol. 29,
Issue. 02,
p.
353.
Liu, Quansheng
2000.
On generalized multiplicative cascades.
Stochastic Processes and their Applications,
Vol. 86,
Issue. 2,
p.
263.
Bachmann, Markus
2000.
Limit theorems for the minimal position in a branching random walk with independent logconcave displacements.
Advances in Applied Probability,
Vol. 32,
Issue. 1,
p.
159.

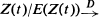 a non-denenerate random variable
a non-denenerate random variable