Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Stadje, Wolfgang
2000.
First exit times for integer valued continuous time markov chains.
Sequential Analysis,
Vol. 19,
Issue. 3,
p.
93.
Kwaśnicki, Mateusz
2020.
Random walks are determined by their trace on the positive half-line.
Annales Henri Lebesgue,
Vol. 3,
Issue. ,
p.
1389.
Vilkas, Timo
2025.
Left-Continuous Random Walk on $${\mathbb {Z}}$$ and the Parity of Its Hitting Times.
Journal of Theoretical Probability,
Vol. 38,
Issue. 4,

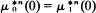 for all
for all 