Article contents
Note on generalizations of Mecke's formula and extensions of H = λG
Published online by Cambridge University Press: 14 July 2016
Abstract
Mecke's formula is concerned with a stationary random measure and shift-invariant measure on a locally compact Abelian group 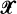 , and relates integrations concerning them to each other. For
, and relates integrations concerning them to each other. For 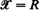 , we generalize this to a pair of random measures which are jointly stationary. The resulting formula extends the so-called Swiss Army formula, which was recently obtained as a generalization for Little's formula. The generalized Mecke formula, which is called GMF, can be also viewed as a generalization of the stationary version of H = λG. Under the stationary and ergodic assumptions, we apply it to derive many sample path formulas which have been known as extensions of H = λG. This will make clear what kinds of probabilistic conditions are sufficient to get them. We also mention a further generalization of Mecke's formula.
, we generalize this to a pair of random measures which are jointly stationary. The resulting formula extends the so-called Swiss Army formula, which was recently obtained as a generalization for Little's formula. The generalized Mecke formula, which is called GMF, can be also viewed as a generalization of the stationary version of H = λG. Under the stationary and ergodic assumptions, we apply it to derive many sample path formulas which have been known as extensions of H = λG. This will make clear what kinds of probabilistic conditions are sufficient to get them. We also mention a further generalization of Mecke's formula.
MSC classification
Information
- Type
- Research Papers
- Information
- Copyright
- Copyright © Applied Probability Trust 1995
Footnotes
Research partly supported by NEC C&C Laboratories.
References
- 3
- Cited by

