Hostname: page-component-cb9f654ff-k7rjm Total loading time: 0 Render date: 2025-08-21T11:29:28.696Z Has data issue: false hasContentIssue false
  • English
  • Français

Monotone utility convergence

Part of: Stochastic analysis Mathematical economics

Published online by Cambridge University Press:  14 July 2016

Stefan Ankirchner
Stefan Ankirchner*
Affiliation:
Imperial College London
*
∗ Postal address: Department of Mathematics, Imperial College London, London SW7 2AZ, UK. Email address: s.ankirchner@imperial.ac.uk
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

We show that the maximal expected utility satisfies a monotone continuity property with respect to increasing information. Let 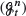be a sequence of increasing filtrations converging to 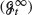, and let u n (x) and u ∞(x) be the maximal expected utilities when investing in a financial market according to strategies adapted to 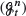and 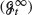, respectively. We give sufficient conditions for the convergence u n (x) → u ∞(x) as n → ∞. We provide examples in which convergence does not hold. Then we consider the respective utility-based prices, πn and π∞, of contingent claims under (G t n ) and (G t ∞). We analyse to what extent πn → π∞ as n → ∞.

Keywords

Utility maximisationinformationenlargement of filtrationsutility-based priceindifference price

MSC classification

Primary: 91B16: Utility theory
Secondary: 60H30: Applications of stochastic analysis (to PDE, etc.)

Information

Type
Research Article
Information
Journal of Applied Probability , Volume 43 , Issue 3 , September 2006 , pp. 622 - 633
Copyright
© Applied Probability Trust 2006 

References

Amendinger, J., Becherer, D. and Schweizer, M. (2003). “A monetary value for initial information in portfolio optimization.” Finance Stoch. 7, 29–46.CrossRefGoogle Scholar
Ankirchner, S. (2005). “{Information and semimartingales}.” {, Humboldt-Universität zu Berlin}. Available at http://edoc.hu-berlin.de/dissertationen/ankirchner-stefan-2005-07-01/PDF/Ankirchner.pdf.Google Scholar
Ankirchner, S. and Imkeller, P. (2005). “Finite utility on financial markets with asymmetric information and structure properties of the price dynamics.” Ann. Inst. H. Poincaré Prob. Statist. 41, 479–503.Google Scholar
Ankirchner, S., Dereich, S. and Imkeller, P. (2006). “The Shannon information of filtrations and the additional logarithmic utility of insiders.” Ann. Prob. 34, 743–778.CrossRefGoogle Scholar
Ansel, J.-P. and Stricker, C. (1992). “Lois de martingale, densités et décomposition de Föllmer–Schweizer.” Ann. Inst. H. Poincaré Prob. Statist. 28, 375–392.Google Scholar
Delbaen, F. and Schachermayer, W. (1994). “A general version of the fundamental theorem of asset pricing.” Math. Ann. 300, 463–520.Google Scholar
Delbaen, F. and Schachermayer, W. (2006).” The Mathematics of Arbitrage. ” Springer, Berlin.Google Scholar
Duffie, D. and Huang, C. (1986). “Multiperiod security markets with differential information: martingales and resolution times.” J. Math. Econom. 15, 283–303.Google Scholar
Föllmer, H. and Imkeller, P. (1993). “Anticipation cancelled by a Girsanov transformation: a paradox on Wiener space.” Ann. Inst. H. Poincaré Prob. Statist. 29, 569–586.Google Scholar
Jeulin, T. (1980).” Semi-Martingales et Grossissement d'une Filtration (Lecture Notes Math. 833).” Springer, Berlin.Google Scholar
Mansuy, R. and Yor, M. (2006).” Random Times and Enlargements of Filtrations in a Brownian Setting (Lecture Notes Math. 1873).” Springer, Berlin.Google Scholar
Pikovsky, I. and Karatzas, I. (1996). “Anticipative portfolio optimization.” Adv. Appl. Prob. 28, 1095–1122.Google Scholar
Protter, P. E. (2004).” Stochastic Integration and Differential Equations (Appl. Math. New York 21), 2nd edn. ” Springer, New York.Google Scholar
Revuz, D. and Yor, M. (1999).” Continuous Martingales and Brownian Motion, 3rd edn. ” Springer, Berlin.Google Scholar
Rockafellar, R. T. (1970).” Convex Analysis (Princeton Math. Ser. 28).” Princeton University Press.CrossRefGoogle Scholar