Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Dudin, Alexander
and
Nishimura, Shoichi
1999.
A BMAP/SM/1 queueing system with Markovian arrival input of disasters.
Journal of Applied Probability,
Vol. 36,
Issue. 3,
p.
868.
Dudin, Alexander
and
Nishimura, Shoichi
1999.
A BMAP/SM/1 queueing system with Markovian arrival input of disasters.
Journal of Applied Probability,
Vol. 36,
Issue. 03,
p.
868.
Artalejo, J.R.
2000.
G-networks: A versatile approach for work removal in queueing networks.
European Journal of Operational Research,
Vol. 126,
Issue. 2,
p.
233.
Dudin, A.N.
and
Karolik, A.V.
2001.
BMAP/SM/1 queue with Markovian input of disasters and non-instantaneous recovery.
Performance Evaluation,
Vol. 45,
Issue. 1,
p.
19.
Gómez-Corral, A.
2002.
On a tandem G-network with blocking.
Advances in Applied Probability,
Vol. 34,
Issue. 3,
p.
626.
Yang, Won S.
Kim, Jin D.
and
Chae, Kyung C.
2002.
ANALYSIS OF M/G/1 STOCHASTIC CLEARING SYSTEMS.
Stochastic Analysis and Applications,
Vol. 20,
Issue. 5,
p.
1083.
Chen, Anyue
Zhang, Hanjun
and
Hou, Zhenting
2002.
Markov Processes and Controlled Markov Chains.
p.
15.
Chen, Anyue
and
Liu, Kai
2003.
Birth-death processes with an instantaneous reflection barrier.
Journal of Applied Probability,
Vol. 40,
Issue. 01,
p.
163.
Shin, Yang Woo
2004.
BMAP/G/1 queue with correlated arrivals of customers and disasters.
Operations Research Letters,
Vol. 32,
Issue. 4,
p.
364.
Atencia, I.
and
Moreno, P.
2004.
The discrete-time Geo/Geo/1 queue with negative customers and disasters.
Computers & Operations Research,
Vol. 31,
Issue. 9,
p.
1537.
Renshaw, Eric
2004.
Metropolis–Hastings from a stochastic population dynamics perspective.
Computational Statistics & Data Analysis,
Vol. 45,
Issue. 4,
p.
765.
2004.
Birth and Death (BDP) Process Models with Applications.
American Journal of Mathematical and Management Sciences,
Vol. 24,
Issue. 1-2,
p.
1.
Semenova, Olga V.
2004.
Optimal control for a BMAP/SM/1 queue with MAP-input of disasters and two operation modes.
RAIRO - Operations Research,
Vol. 38,
Issue. 2,
p.
153.
Chen, Anyue
and
Renshaw, Eric
2004.
Markovian bulk-arriving queues with state-dependent control at idle time.
Advances in Applied Probability,
Vol. 36,
Issue. 2,
p.
499.
Gillespie, Colin S
and
Renshaw, Eric
2005.
The evolution of a batch-immigration death process subject to counts.
Proceedings of the Royal Society A: Mathematical, Physical and Engineering Sciences,
Vol. 461,
Issue. 2057,
p.
1563.
Chen, Anyue
Li, Junping
and
Ramesh, N. I.
2005.
Uniqueness and Extinction of Weighted Markov Branching Processes.
Methodology and Computing in Applied Probability,
Vol. 7,
Issue. 4,
p.
489.
Shin, Yang-Woo
2006.
AN MMAP[3]/PH/1 QUEUE WITH NEGATIVE CUSTOMERS AND DISASTERS.
Bulletin of the Korean Mathematical Society,
Vol. 43,
Issue. 2,
p.
277.
Yi, Xeung Won
Kim, Jin Dong
Choi, Dae Won
and
Chae, Kyung Chul
2007.
The Geo/G/1 Queue with Disasters and Multiple Working Vacations.
Stochastic Models,
Vol. 23,
Issue. 4,
p.
537.
Krishna Kumar, B.
Krishnamoorthy, A.
Pavai Madheswari, S.
and
Sadiq Basha, S.
2007.
Transient analysis of a single server queue with catastrophes, failures and repairs.
Queueing Systems,
Vol. 56,
Issue. 3-4,
p.
133.
Gillespie, Colin S.
and
Renshaw, Eric
2007.
An improved saddlepoint approximation.
Mathematical Biosciences,
Vol. 208,
Issue. 2,
p.
359.

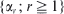 when idle. A general resolvent approach is used to derive occupation probabilities and high-order moments. This powerful technique is not only considerably easier to apply than a standard direct attack on the forward p.g.f. equation, but it also implicitly yields necessary and sufficient conditions for recurrence, positive recurrence and transience.
when idle. A general resolvent approach is used to derive occupation probabilities and high-order moments. This powerful technique is not only considerably easier to apply than a standard direct attack on the forward p.g.f. equation, but it also implicitly yields necessary and sufficient conditions for recurrence, positive recurrence and transience.