No CrossRef data available.
Article contents
A martingale approach to the PASTA property
Published online by Cambridge University Press: 14 July 2016
Abstract
It is known (Weizsäcker and Winkler (1990)) that for bounded predictable functions H and a Poisson process with jump times 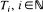
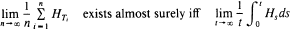 exists almost surely, and that in this case both limits are equal. Here we relax the boundedness condition on H. Our tool is a law of large numbers for local L 2-martingales. We show by examples that our condition is close to optimal. Furthermore we indicate a generalization to point processes on more general spaces. The above property is called PASTA (‘Poisson arrivals see time averages') and is heavily used in queueing theory.
exists almost surely, and that in this case both limits are equal. Here we relax the boundedness condition on H. Our tool is a law of large numbers for local L 2-martingales. We show by examples that our condition is close to optimal. Furthermore we indicate a generalization to point processes on more general spaces. The above property is called PASTA (‘Poisson arrivals see time averages') and is heavily used in queueing theory.
Keywords
MSC classification
Information
- Type
- Short Communications
- Information
- Copyright
- Copyright © Applied Probability Trust 1993
References
Feller, W. (1943) The general form of the so-called law of the iterated logarithm. Trans. Amer. Math. Soc. 54, 373–402.CrossRefGoogle Scholar
Hall, P. and Heyde, C. C. (1980) Martingale Limit Theory and its Application. Academic Press, New York.Google Scholar
Jacod, J. and Shiryaev, A. N. (1987) Limit Theorems for Stochastic Processes. Springer-Verlag, Berlin.Google Scholar
Liptser, R. Sh. (1980) A strong law of large numbers for local martingales. Stochastics
3, 217–228.CrossRefGoogle Scholar
Miyazawa, M. and Wolff, R. W. (1990) Further results on ASTA for general stationary processes and related problems. J. Appl. Prob.
28, 792–804.Google Scholar
Protter, P. (1990) Stochastic Integration and Differential Equations. Springer-Verlag, Berlin.Google Scholar
Rogers, L. C. G. and Williams, D. (1987) Diffusions, Markov Processes and Martingales
, Vol. 2. Wiley, Chichester.Google Scholar

