Hostname: page-component-6bb9c88b65-kzqxb Total loading time: 0 Render date: 2025-07-18T08:29:52.082Z Has data issue: false hasContentIssue false
  • English
  • Français

Martingale approach to gambler’s ruin problem for correlated randomwalks

Part of: Stochastic processes Markov processes

Published online by Cambridge University Press:  15 July 2025

Vladimir Pozdnyakov
Vladimir Pozdnyakov*
Affiliation:
University of Connecticut
*
*Postal address: Department of Statistics, University of Connecticut, 215 Glenbrook Road, Storrs, CT 06269-4120. Email: vladimir.pozdnyakov@uconn.edu
Get access Rights & Permissions [Opens in a new window]

Abstract

The gambler’s ruin problem for correlated random walks (CRWs), both with and without delays, is addressed using the optional stopping theorem for martingales. We derive closed-form expressions for the ruin probabilities and the expected game duration for CRWs with increments 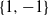$\{1,-1\}$ and for symmetric CRWs with increments 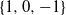$\{1,0,-1\}$ (CRWs with delays). Additionally, a martingale technique is developed for general CRWs with delays. The gambler’s ruin probability for a game involving bets on two arbitrary patterns is also examined.

Keywords

Gambler’s ruinMarkov chainoptional stopping theorem

MSC classification

Primary: 60G42: Martingales with discrete parameter
Secondary: 60J10: Markov chains (discrete-time Markov processes on discrete state spaces)

Information

Type
Original Article
Information
Journal of Applied Probability , First View , pp. 1 - 13
Check for updates
Copyright
© The Author(s), 2025. Published by Cambridge University Press on behalf of Applied Probability Trust

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Article purchase

Temporarily unavailable

References

Allaart, P. (2004). Stopping the maximum of a correlated random walk, with cost for observation. J. Appl. Prob. 41, 998–1007.10.1239/jap/1101840546CrossRefGoogle Scholar
Chen, A. and Renshaw, E. (1992). The Gillis–Domb–Fisher correlated random walk. J. Appl. Prob. 29, 792–813.10.2307/3214713CrossRefGoogle Scholar
Feller, W. (1968). An Introduction to Probability Theory and its Applications, Vol. I, 3rd edn. John Wiley, New York.Google Scholar
Fuh, C.-D. (2004). Uniform Markov renewal theory and ruin probabilities in Markov random walks. Ann. Appl. Prob. 14, 1202–1241.10.1214/105051604000000260CrossRefGoogle Scholar
Gardner, B., McClintock, B. T., Converse, S. J. and Hostetter, N. J. (2022). Integrated animal movement and spatial capture–recapture models: Simulation, implementation, and inference. Ecology 103, e3771.10.1002/ecy.3771CrossRefGoogle ScholarPubMed
Gillis, J. (1955). Correlated random walk. Math. Proc. Camb. Phil. Soc. 51, 639–651.Google Scholar
Grama, I., Lauvergnat, R. and Page, É. L. (2018). Limit theorems for Markov walks conditioned to stay positive under a spectral gap assumption. Ann. Prob. 46, 1807–1877.10.1214/17-AOP1197CrossRefGoogle Scholar
Guerriero, M., Pozdnyakov, V., Glaz, J. and Willett, P. (2010). A repeated significance test with applications to sequential detection in sensor networks. IEEE Trans. Sig. Proc. 58, 3426–3435.10.1109/TSP.2010.2046074CrossRefGoogle Scholar
Guibas, L. J. and Odlyzko, A. M. (1981). String overlaps, pattern matching, and nontransitive games. J. Combinatorial Theory A 30, 183–208.10.1016/0097-3165(81)90005-4CrossRefGoogle Scholar
Gut, A. (2013). The gambler’s ruin problem with delays. Statist. Prob. Lett. 83, 2549–2552.10.1016/j.spl.2013.07.013CrossRefGoogle Scholar
Gut, A. and Stadtmüller, U. (2021). Variations of the elephant random walk. J. Appl. Prob. 58, 805–829.10.1017/jpr.2021.3CrossRefGoogle Scholar
Gut, A. and Stadtmüller, U. (2023). Elephant random walks; a review. Ann. Univ. Sci. Budapest Sect. Comput. 54, 171–198.Google Scholar
Konno, N. (2009). Limit theorems and absorption problems for one-dimensional correlated random walks. Stoch. Models 25, 28–49.10.1080/15326340802640941CrossRefGoogle Scholar
Lal, R. and Bhat, U. N. (1989). Some explicit results for correlated random walks. J. Appl. Prob. 26, 757–766.10.2307/3214380CrossRefGoogle Scholar
Li, S.-Y. R. (1980). A martingale approach to the study of occurrence of sequence patterns in repeated experiments. Ann. Prob. 8, 1171–1176.10.1214/aop/1176994578CrossRefGoogle Scholar
Mohan, C. (1955). The gambler’s ruin problem with correlation. Biometrika 42, 486–493.10.1093/biomet/42.3-4.486CrossRefGoogle Scholar
Mukherjea, A. and Steele, D. A. (1987). Occupation probability of a correlated random walk and a correlated ruin problem. Statist. Prob. Lett. 5, 105–111.10.1016/0167-7152(87)90064-2CrossRefGoogle Scholar
Solov’ev, A. D. (1966). A combinatorial identity and its application to the problem on the first occurrence of a rare event. Teor. Verojatnost. i Primenen. 11, 313–320.Google Scholar
Steele, J. M. (2001). Stochastic Calculus and Financial Applications (Appl. Math. (New York) 45). Springer, New York.10.1007/978-1-4684-9305-4CrossRefGoogle Scholar