Article contents
Limit theorems for out guesses with mean-guided second guessing
Published online by Cambridge University Press: 14 July 2016
Abstract
A second guesser, G2, proposes to guess ‘smaller' or ‘larger' on each of n contests, i, according as 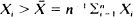 , or
, or 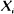 where Xi, i = 1, ···, n are the revealed guesses of the first guesser, G1. G2 wins contest i if his assertion about the size of the target quantity θ i , is more accurate than that of G1, Xi, i = 1, ···, n. Otherwise G 1 is the winner. Laws of large numbers are derived for G2's win totals for arbitrary configurations of θ i . Limiting distributions are obtained for the first guesser's win totals in two special cases, the first where the θ i are highly concentrated and the second where they are widely dispersed. G2 enjoys an enormous advantage over G1 in the former case, as intuition would suggest.
where Xi, i = 1, ···, n are the revealed guesses of the first guesser, G1. G2 wins contest i if his assertion about the size of the target quantity θ i , is more accurate than that of G1, Xi, i = 1, ···, n. Otherwise G 1 is the winner. Laws of large numbers are derived for G2's win totals for arbitrary configurations of θ i . Limiting distributions are obtained for the first guesser's win totals in two special cases, the first where the θ i are highly concentrated and the second where they are widely dispersed. G2 enjoys an enormous advantage over G1 in the former case, as intuition would suggest.
Information
- Type
- Research Papers
- Information
- Copyright
- Copyright © Applied Probability Trust 1982
Footnotes
This research was supported by the National Science Foundation of the United States under grants NSF MCS-80-03568 and NSF MCS-782-4175.
References
- 5
- Cited by

