No CrossRef data available.
Article contents
Limit distributions of the number of renewals and waiting times
Published online by Cambridge University Press: 14 July 2016
Abstract
Let {X n} be an infinite sequence of independent non-negative random variables. Let the distribution function of Xi , i = 1, 2, …, be either F 1 or F 2 where F 1 and F 2 are distinct. Set Sn = X 1 + X 2 + … + Xn and for t > 0 define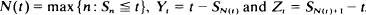 
and Zt = SN (t)+1 – t. The limit distributions of N(t), Yt and Zt as t → ∞ are obtained when F 1 and F 2 are in the domains of attraction of stable laws with exponents α 1 and α 2 , respectively and Sn properly normalised has the composition of these two stable laws as its limit distribution.
Keywords
Information
- Type
- Research Papers
- Information
- Copyright
- Copyright © Applied Probability Trust 1976
References
[1]
Gnedenko, B. V. and Kolmogorov, A. N. (1954)
Limit Distributions for Sums of Independent Random Variables.
Addison-Wesley, Cambridge, Mass.Google Scholar
[2]
Feller, W. (1966)
An Introduction to Probability Theory and its Applications
, Vol. II. Wiley, New York.Google Scholar
[3]
Pakshirajan, R. P. and Vasudeva, R.
On the limit distribution of sums of independent random variables. Unpublished.Google Scholar
[5]
Smith, W. L. (1968) On infinitely divisible laws and a renewal theorem for non-negative random variables.
Ann. Math. Statist.
39, 139–154.CrossRefGoogle Scholar
[6]
Sreehari, M. (1970) On a class of limit distributions for normalized sums of independent random variables.
Theor. Prob. Appl.
15, 258–281.CrossRefGoogle Scholar