No CrossRef data available.
Article contents
A large deviation theorem for a supercritical super-Brownian motion with absorption
Published online by Cambridge University Press: 02 May 2023
Abstract
We consider a one-dimensional superprocess with a supercritical local branching mechanism  $\psi$, where particles move as a Brownian motion with drift
$\psi$, where particles move as a Brownian motion with drift 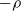 $-\rho$ and are killed when they reach the origin. It is known that the process survives with positive probability if and only if
$-\rho$ and are killed when they reach the origin. It is known that the process survives with positive probability if and only if 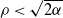 $\rho<\sqrt{2\alpha}$, where
$\rho<\sqrt{2\alpha}$, where 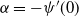 $\alpha=-\psi'(0)$. When
$\alpha=-\psi'(0)$. When 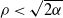 $\rho<\sqrt{2 \alpha}$, Kyprianou et al. [18] proved that
$\rho<\sqrt{2 \alpha}$, Kyprianou et al. [18] proved that 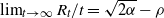 $\lim_{t\to \infty}R_t/t =\sqrt{2\alpha}-\rho$ almost surely on the survival set, where
$\lim_{t\to \infty}R_t/t =\sqrt{2\alpha}-\rho$ almost surely on the survival set, where 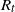 $R_t$ is the rightmost position of the support at time t. Motivated by this work, we investigate its large deviation, in other words, the convergence rate of
$R_t$ is the rightmost position of the support at time t. Motivated by this work, we investigate its large deviation, in other words, the convergence rate of 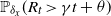 $\mathbb{P}_{\delta_x} (R_t >\gamma t+\theta)$ as
$\mathbb{P}_{\delta_x} (R_t >\gamma t+\theta)$ as 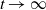 $t \to \infty$, where
$t \to \infty$, where  $\gamma >\sqrt{2 \alpha} -\rho$,
$\gamma >\sqrt{2 \alpha} -\rho$, 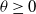 $\theta \ge 0$. As a by-product, a related Yaglom-type conditional limit theorem is obtained. Analogous results for branching Brownian motion can be found in Harris et al. [13].
$\theta \ge 0$. As a by-product, a related Yaglom-type conditional limit theorem is obtained. Analogous results for branching Brownian motion can be found in Harris et al. [13].
MSC classification
Information
- Type
- Original Article
- Information
- Copyright
- © The Author(s), 2023. Published by Cambridge University Press on behalf of Applied Probability Trust


