Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Glynn, Peter W.
2011.
On exponential limit laws for hitting times of rare sets for Harris chains and processes.
Journal of Applied Probability,
Vol. 48,
Issue. A,
p.
319.

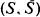 . Let
. Let 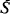 such that
such that 