Hostname: page-component-745bb68f8f-d8cs5 Total loading time: 0 Render date: 2025-01-11T23:48:23.618Z Has data issue: false hasContentIssue false
  • English
  • Français

A functional equation and its application to the characterization of the Weibull and stable distributions

Published online by Cambridge University Press:  14 July 2016

Y. H. Wang
Y. H. Wang*
Affiliation:
Concordia University, Montreal, Canada
Get access Rights & Permissions [Opens in a new window]

Abstract

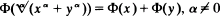The Cauchy functional equation Φ(x + y) = Φ(x) + Φ(y) is generalized to the form , assuming Φ is left- or right- continuous. This result is used to obtain (1) a characterization of the Weibull distribution, in the spirit of the memoryless property of the exponential distribution, by 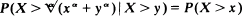, for all x, y ≧ 0;(2) a characterization of the symmetric α-stable distribution by the equidistribution of linear statistics.

Keywords

CAUCHY FUNCTIONAL EQUATIONEXPONENTIAL DISTRIBUTIONMEMORYLESS PROPERTYWEIBULL DISTRIBUTIONINCREASING (DECREASING) FAILURE RATECHARACTERIZATIONSTABLE DISTRIBUTIONEQUIDISTRIBUTIONLINEAR STATISTICS
Type
Short Communications
Information
Journal of Applied Probability , Volume 13 , Issue 2 , June 1976 , pp. 385 - 391
Copyright
Copyright © Applied Probability Trust 1976 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

[1] Barlow, R. E. and Proschan, F. (1975) Statistical Theory of Reliability and Life Testing — Probability Models. Holt, Rinehart and Winston, New York.Google Scholar
[2] Beer, S. and Lukacs, E. (1973) Characterization of the normal distribution by suitable transformations. J. Appl. Prob. 10, 100–108.Google Scholar
[3] Eaton, M. L. (1966) Characterization of distributions by identical distribution of linear forms. J. Appl. Prob. 3, 481–494.Google Scholar
[4] Feller, W. (1968) An Introduction to Probability Theory and Its Applications. Vol. 1, 3rd edn, Wiley, New York.Google Scholar
[5] Kagan, A. M., Linnik, Y. U. and Rao, C. R. (1973) Characterization Problems in Mathematical Statistics. (English translation by Ramachandran, B.), Wiley, New York.Google Scholar
[6] Laha, R. G. and Lukacs, E. (1965) On a linear form whose distribution is identical with that of a monomial. Pacific J. Math. 15, 207–214.CrossRefGoogle Scholar
[7] Lévy, P. (1954) Théorie de l'Addition des Variables Aléatoires. Gauthier-Villars, Paris.Google Scholar
[8] Lukacs, E. (1956) Characterization of populations by properties of suitable statistics. Proc. 3rd Berkeley Symp. Math. Statist. Prob. 2, 195–214.Google Scholar
[9] Marsaglia, G. and Tubilla, A. (1975) A note on the “lack of memory” property of the exponential distribution. Ann. Prob. 3, 353–354.Google Scholar
[10] Sierpiński, W. (1920) Sur l'équation fonctionelle f (x + y) = f (x) + f (y) . Fund. Math. 1, 116–122.Google Scholar