Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Hannan, E.J
1973.
Multivariate time series analysis.
Journal of Multivariate Analysis,
Vol. 3,
Issue. 4,
p.
395.
Hannan, E.
1974.
Time series analysis.
IEEE Transactions on Automatic Control,
Vol. 19,
Issue. 6,
p.
706.
BRILLINGER, DAVID R.
1978.
Vol. 1,
Issue. ,
p.
33.
Bolt, B. A.
and
Brillinger, D. R.
1979.
Estimation of uncertainties in eigenspectral estimates from decaying geophysical time series.
Geophysical Journal International,
Vol. 59,
Issue. 3,
p.
593.
Ong, B. G.
and
Campbell, L. L.
1979.
Estimation of frequencies of sinusoids in the presence of noise.
Canadian Journal of Statistics,
Vol. 7,
Issue. 1,
p.
11.
Brillinger, David R.
1980.
THE COMPARISON OF LEAST SQUARES AND THIRD‐ORDER PERIODOGRAM PROCEDURES IN THE ESTIMATION OF BIFREQUENCY.
Journal of Time Series Analysis,
Vol. 1,
Issue. 2,
p.
95.
Vere-Jones, D.
1982.
On the estimation of frequency in point-process data.
Journal of Applied Probability,
Vol. 19,
Issue. A,
p.
383.
Rao, T.S.
and
Yar, M.
1982.
Statistical analysis of frequency modulated signals.
Vol. 7,
Issue. ,
p.
1042.
Thomson, D.J.
1982.
Spectrum estimation and harmonic analysis.
Proceedings of the IEEE,
Vol. 70,
Issue. 9,
p.
1055.
Hasan, T.
1982.
NONLINEAR TIME SERIES REGRESSION FOR A CLASS OF AMPLITUDE MODULATED CONSINUSOIDS.
Journal of Time Series Analysis,
Vol. 3,
Issue. 2,
p.
109.
An, Hong-Zhi
Chen, Zhao-Guo
and
Hannan, E.J
1983.
The maximum of the periodogram.
Journal of Multivariate Analysis,
Vol. 13,
Issue. 3,
p.
383.
Isokawa, Y.
1983.
Estimation of frequency by random sampling.
Annals of the Institute of Statistical Mathematics,
Vol. 35,
Issue. 2,
p.
201.
Brillinger, David R.
1986.
Regression for randomly sampled spatial series: the trigonometric case.
Journal of Applied Probability,
Vol. 23,
Issue. A,
p.
275.
Hannan, E.J.
and
Mackisack, M.
1986.
A law of the iterated logarithm for an estimate of frequency.
Stochastic Processes and their Applications,
Vol. 22,
Issue. 1,
p.
103.
Brillinger, David R.
1987.
Advances in the Statistical Sciences: Applied Probability, Stochastic Processes, and Sampling Theory.
p.
75.
Hannan, E. J.
and
Quinn, B. G.
1989.
THE RESOLUTION OF CLOSELY ADJACENT SPECTRAL LINES.
Journal of Time Series Analysis,
Vol. 10,
Issue. 1,
p.
13.
Chiu, Shean-Tsong
1990.
Peak-insensitive parametric spectrum estimation.
Stochastic Processes and their Applications,
Vol. 35,
Issue. 1,
p.
121.
Truong-Van, B.
1990.
A New Approach to Frequency Analysis with Amplified Harmonics.
Journal of the Royal Statistical Society Series B: Statistical Methodology,
Vol. 52,
Issue. 1,
p.
203.
Maiwald, D.
and
Bohme, J.F.
1992.
Estimation of seismic wave parameters by nonlinear regression.
p.
512.
Kahn, M. H.
Mackisack, M. S.
Osborne, M. R.
and
Smyth, G. K.
1992.
On the Consistency of Prony's Method and Related Algorithms.
Journal of Computational and Graphical Statistics,
Vol. 1,
Issue. 4,
p.
329.

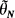 , satisfies
, satisfies 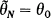 for
for 