Article contents
Equality of critical densities in continuum percolation
Published online by Cambridge University Press: 14 July 2016
Abstract
Consider a homogeneous Poisson process in 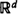 with density ρ, and add the origin as an extra point. Now connect any two points x and y of the process with probability g(x − y), independently of the point process and all other pairs, where g is a function which depends only on the Euclidean distance between x and y, and which is nonincreasing in the distance. We distinguish two critical densities in this model. The first is the infimum of all densities for which the cluster of the origin is infinite with positive probability, and the second is the infimum of all densities for which the expected size of the cluster of the origin is infinite. It is known that if
with density ρ, and add the origin as an extra point. Now connect any two points x and y of the process with probability g(x − y), independently of the point process and all other pairs, where g is a function which depends only on the Euclidean distance between x and y, and which is nonincreasing in the distance. We distinguish two critical densities in this model. The first is the infimum of all densities for which the cluster of the origin is infinite with positive probability, and the second is the infimum of all densities for which the expected size of the cluster of the origin is infinite. It is known that if 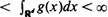 , then the two critical densities are non-trivial, i.e. bounded away from 0 and ∞. It is also known that if g is of the form
, then the two critical densities are non-trivial, i.e. bounded away from 0 and ∞. It is also known that if g is of the form 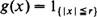 , for some r > 0, then the two critical densities coincide. In this paper we generalize this result and show that under the integrability condition mentioned above the two critical densities are always equal.
, for some r > 0, then the two critical densities coincide. In this paper we generalize this result and show that under the integrability condition mentioned above the two critical densities are always equal.
Keywords
MSC classification
Information
- Type
- Research Papers
- Information
- Copyright
- Copyright © Applied Probability Trust 1995
References
- 4
- Cited by

