No CrossRef data available.
Article contents
Drift vectors are not sufficient to determine recurrence of a Markov chain on ℤ3 +
Part of:
Markov processes
Published online by Cambridge University Press: 14 July 2016
Abstract
For a Markov chain in 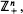 n = 2, drift vectors (conditional expected jumps) on the interior and the boundaries distinguish between recurrence and transience. The result of this paper is that the analogous proposition in the n = 3 case fails.
n = 2, drift vectors (conditional expected jumps) on the interior and the boundaries distinguish between recurrence and transience. The result of this paper is that the analogous proposition in the n = 3 case fails.
Keywords
MSC classification
Information
- Type
- Research Article
- Information
- Copyright
- Copyright © Applied Probability Trust 1994
References
Fayolle, G. (1989) On random walks arising in queueing systems: ergodicity and transience via quadratic forms as Lyapounov functions – Part I.
Queueing Systems
5, 167–184.CrossRefGoogle Scholar
Foster, F. G. (1953) On the stochastic matrices associated with certain queueing processes.
Ann. Math. Statist.
24, 355–360.CrossRefGoogle Scholar
Malyshev, V. A. (1972) Classification of two-dimensional positive random walks and almost linear semi-martingales.
Sov. Math. Dokl.
13, 136–139.Google Scholar
Rosenkrantz, W. (1989) Ergodicity conditions for two-dimensional Markov chains on the positive quadrant.
Prob. Theory Rel. Fields
83, 309–319.Google Scholar

