Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Vatutin, V. A.
and
Zubkov, A. M.
1993.
Branching processes. II.
Journal of Soviet Mathematics,
Vol. 67,
Issue. 6,
p.
3407.
González, M.
Molina, M.
and
Del Puerto, I.
2002.
On the class of controlled branching processes with random control functions.
Journal of Applied Probability,
Vol. 39,
Issue. 04,
p.
804.
González, M.
Molina, M.
and
del Puerto, I.
2003.
On the geometric growth in controlled branching processes with random control function.
Journal of Applied Probability,
Vol. 40,
Issue. 04,
p.
995.
González, M.
Molina, M.
and
del Puerto, I.
2004.
On the Controlled Galton-Watson Process with Random Control Function.
Journal of Mathematical Sciences,
Vol. 121,
Issue. 5,
p.
2629.
González, M.
Molina, M.
and
del Puerto, I.
2004.
Limiting distribution for subcritical controlled branching processes with random control function.
Statistics & Probability Letters,
Vol. 67,
Issue. 3,
p.
277.
González, M.
Molina, M.
and
del Puerto, I.
2005.
Asymptotic behaviour of critical controlled branching processes with random control functions.
Journal of Applied Probability,
Vol. 42,
Issue. 02,
p.
463.
González, Miguel
Molina, Manuel
and
Del Puerto, Inés
2005.
On L2-convergence of controlled branching processes with random control function.
Bernoulli,
Vol. 11,
Issue. 1,
Drmota, Michael
Louchard, Guy
and
Yanev, Nickolay M.
2006.
Analysis of a Recurrence Related to Critical Nonhomogeneous Branching Processes.
Stochastic Analysis and Applications,
Vol. 24,
Issue. 1,
p.
37.
Gonzalez, M.
Molina, M.
and
del Puerto, I.
2006.
Some limit results for controlled branching processes with random control function*.
Journal of Mathematical Sciences,
Vol. 138,
Issue. 1,
p.
5396.
Martínez, R.
Mota, M.
and
del Puerto, I.
2009.
On asymptotic posterior normality for controlled branching processes.
Statistics,
Vol. 43,
Issue. 4,
p.
367.
2010.
Introduction to Stochastic Models.
p.
343.
González, Miguel
and
del Puerto, Inés M.
2012.
Diffusion Approximation of an Array of Controlled Branching Processes.
Methodology and Computing in Applied Probability,
Vol. 14,
Issue. 3,
p.
843.
Chandra, Tapas Kumar
2012.
The Borel-Cantelli Lemma.
Vol. 2,
Issue. ,
p.
51.
González, Miguel
Gutiérrez, Cristina
Martínez, Rodrigo
and
del Puerto, Inés M.
2013.
Bayesian inference for controlled branching processes through MCMC and ABC methodologies.
Revista de la Real Academia de Ciencias Exactas, Fisicas y Naturales. Serie A. Matematicas,
Vol. 107,
Issue. 2,
p.
459.
Davie, George
2013.
Decidable lim sup and Borel–Cantelli-like lemmas for random sequences.
Statistics & Probability Letters,
Vol. 83,
Issue. 1,
p.
278.
Bruss, F. Thomas
2014.
Grenzen einer jeden Gesellschaft.
Jahresbericht der Deutschen Mathematiker-Vereinigung,
Vol. 116,
Issue. 3,
p.
137.
Bruss, F. Thomas
and
Duerinckx, Mitia
2015.
Resource dependent branching processes and the envelope of societies.
The Annals of Applied Probability,
Vol. 25,
Issue. 1,
Steel, Mike
2015.
Reflections on the extinction–explosion dichotomy.
Theoretical Population Biology,
Vol. 101,
Issue. ,
p.
61.
Biró, Csaba
and
Darji, Udayan B.
2018.
Generating Infinite Random Graphs.
Proceedings of the Edinburgh Mathematical Society,
Vol. 61,
Issue. 3,
p.
847.
Terelius, Hakan
and
Johansson, Karl Henrik
2018.
Peer-to-Peer Gradient Topologies in Networks With Churn.
IEEE Transactions on Control of Network Systems,
Vol. 5,
Issue. 4,
p.
2085.
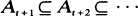 for some
for some 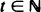 . We will see that this property of (An ) may frequently be assumed without loss of generality. We also disclose a useful duality which allows straightforward conclusions without selecting independent sequences. A simple random walk example and a new result in the theory of ϕ -branching processes will show the tractability of the method.
. We will see that this property of (An ) may frequently be assumed without loss of generality. We also disclose a useful duality which allows straightforward conclusions without selecting independent sequences. A simple random walk example and a new result in the theory of ϕ -branching processes will show the tractability of the method.
