Hostname: page-component-cb9f654ff-pvkqz Total loading time: 0 Render date: 2025-08-26T05:48:45.115Z Has data issue: false hasContentIssue false
  • English
  • Français

Bounds for expected supremum of fractional Brownian motion with drift

Part of: Stochastic processes Computer system organization

Published online by Cambridge University Press:  23 June 2021

Krzysztof Bisewski Open the ORCID record for Krzysztof Bisewski [Opens in a new window] ,
Krzysztof Dębicki  and
Michel Mandjes
Krzysztof Bisewski*
Affiliation:
Université de Lausanne
Krzysztof Dębicki*
Affiliation:
Wrocław University
Michel Mandjes*
Affiliation:
University of Amsterdam
*
*Postal address: Quartier UNIL-Chamberonne, Bâtiment Extranef, 1015 Lausanne, Switzerland. Email address: kbisewski@gmail.com
**Postal address: pl. Grunwaldzki 2/4, 50-384 Wrocław, Poland.
***Postal address: Science Park 904, 1098 XH Amsterdam, The Netherlands.
Get access Rights & Permissions [Opens in a new window]

Abstract

We provide upper and lower bounds for the mean 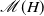$\mathscr{M}(H)$ of 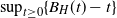$\sup_{t\geq 0} \{B_H(t) - t\}$, with 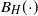$B_H(\!\cdot\!)$ a zero-mean, variance-normalized version of fractional Brownian motion with Hurst parameter 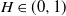$H\in(0,1)$. We find bounds in (semi-) closed form, distinguishing between 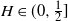$H\in(0,\frac{1}{2}]$ and 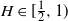$H\in[\frac{1}{2},1)$, where in the former regime a numerical procedure is presented that drastically reduces the upper bound. For 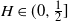$H\in(0,\frac{1}{2}]$, the ratio between the upper and lower bound is bounded, whereas for 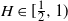$H\in[\frac{1}{2},1)$ the derived upper and lower bound have a strongly similar shape. We also derive a new upper bound for the mean of 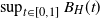$\sup_{t\in[0,1]} B_H(t)$, 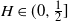$H\in(0,\frac{1}{2}]$, which is tight around 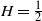$H=\frac{1}{2}$.

Keywords

Fractional Brownian motionextreme valuebounds

MSC classification

Primary: 60G22: Fractional processes, including fractional Brownian motion
Secondary: 60G15: Gaussian processes 68M20: Performance evaluation; queueing; scheduling

Information

Type
Original Article
Information
Journal of Applied Probability , Volume 58 , Issue 2 , June 2021 , pp. 411 - 427
Check for updates
Copyright
© The Author(s), 2021. Published by Cambridge University Press on behalf of Applied Probability Trust

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Article purchase

Temporarily unavailable

References

Adler, R. (1990). An Introduction to Continuity, Extrema, and Related Topics for General Gaussian Processes. Institute of Mathematical Statistics, Hayward, CA.Google Scholar
Adler, R. and Taylor, J. E. (2009). Random Fields and Geometry. Springer.Google Scholar
Asmussen, S. and Albrecher, H. (2010). Ruin Probabilities. World Scientific, Singapore.10.1142/7431CrossRefGoogle Scholar
Baillie, R. (1996). Long memory processes and fractional integration in econometrics. J. Econometrics 73, 5–59.10.1016/0304-4076(95)01732-1CrossRefGoogle Scholar
Borovkov, K., Mishura, Y., Novikov, A. and Zhitlukhin, M. (2018). New bounds for expected maxima of fractional Brownian motion. Statist. Prob. Lett. 137, 142–147.10.1016/j.spl.2018.01.025CrossRefGoogle Scholar
Borovkov, K., Mishura, Y., Novikov, A. and Zhitlukhin, M. (2017). Bounds for expected maxima of Gaussian processes and their discrete approximations. Stochastics 89, 21–37.CrossRefGoogle Scholar
Caspi, A., Granek, R. and Elbaum, M. (2000). Enhanced diffusion in active intracellular transport. Phys. Rev. Lett. 85, 5655.CrossRefGoogle ScholarPubMed
Cont, R. (2005). Long-range dependence in financial markets. In Fractals in Engineering: New Trends in Theory and Applications, eds LÉvy-VÉhel, J. and Lutton, E., pp. 159–179. Springer, New York.Google Scholar
Dębicki, K. (2002). Ruin probability for Gaussian integrated processes. Stoch. Process. Appl. 98, 151–174.CrossRefGoogle Scholar
Dębicki, K. (2001). Asymptotics of the supremum of scaled Brownian motion. Prob. Math. Statist. 21, 199–212.Google Scholar
Dębicki, K. and Mandjes, M. (2003). Exact overflow asymptotics for queues with many Gaussian inputs. J. Appl. Prob. 40, 704–720.10.1239/jap/1059060897CrossRefGoogle Scholar
Dębicki, K., Kosiński, K., Mandjes, M. and Rolski, T. (2010). Extremes of multidimensional Gaussian processes. Stoch. Process. Appl. 120, 2289–2301.CrossRefGoogle Scholar
Dębicki, K., Michna, Z. and Rolski, T. (2001). On the supremum from Gaussian processes over infinite horizon. Prob. Math. Statist. 18, 83–100.Google Scholar
Dieker, A. (2005). Extremes of Gaussian processes over an infinite horizon. Stoch. Process. Appl. 115, 207–248.CrossRefGoogle Scholar
Duffield, N. and O’Connell, N. (1995). Large deviations and overflow probabilities for general single-server queue, with applications. Math. Proc. Camb. Phil. Soc. 118, 363–374.CrossRefGoogle Scholar
Hüsler, J. and Piterbarg, V. (1999). Extremes of a certain class of Gaussian processes. Stoch. Process. Appl. 83, 257–271.10.1016/S0304-4149(99)00041-1CrossRefGoogle Scholar
Hüsler, J. and Piterbarg, V. (2004). On the ruin probability for physical fractional Brownian motion. Stoch. Process. Appl. 113, 315–332.10.1016/j.spa.2004.04.004CrossRefGoogle Scholar
Malsagov, A. and Mandjes, M. (2019). Approximations for reflected fractional Brownian motion. Phys. Rev. E 100, 032120.10.1103/PhysRevE.100.032120CrossRefGoogle ScholarPubMed
Mandjes, M. (2007). Large Deviations for Gaussian Queues. Wiley, Chichester.10.1002/9780470515099CrossRefGoogle Scholar
Mandjes, M. and van Uitert, M. (2005). Sample-path large deviations for tandem and priority queues with Gaussian inputs. Ann. Appl. Prob. 15, 1193–1226.10.1214/105051605000000133CrossRefGoogle Scholar
Mandjes, M., Mannersalo, P., Norros, I. and van Uitert, M. (2006). Large deviations of infinite intersections of events in Gaussian processes. Stoch. Process. Appl. 116, 1269–1293.CrossRefGoogle Scholar
Mandjes, M., Norros, I. and Glynn, P. (2009). On convergence to stationarity of fractional Brownian storage. Ann. Appl. Prob. 18, 1385–1403.Google Scholar
Massoulié, L. and Simonian, A. (1999). Large buffer asymptotics for the queue with FBM input. J. Appl. Prob. 36, 894–906.10.1239/jap/1032374642CrossRefGoogle Scholar
Meroz, Y. and Sokolov, I. (2015). A toolbox for determining subdiffusive mechanisms. Phys. Rep. 573, 1–30.CrossRefGoogle Scholar
Metzler, R., Jeon, J.-H., Cherstvya, A. and Barkaid, E. (2014). Anomalous diffusion models and their properties: non-stationarity, non-ergodicity, and ageing at the centenary of single particle tracking. Phys. Chem. Chem. Phys. 16, 24128–24164.10.1039/C4CP03465ACrossRefGoogle Scholar
Montanari, A.. (2003). Long-range dependence in hydrology. In Theory and Applications of Long-Range Dependence, eds Doukhan, P., Oppenheim, G. and Taqqu, M., pp. 461–472. Birkhäuser, Boston, MA.Google Scholar
Narayan, O. (1998). Exact asymptotic queue length distribution for fractional Brownian traffic. Adv. Performance Analysis 1, 39–63.Google Scholar
Norros, I. (2019). Private communication.Google Scholar
Piterbarg, V. (1996). Asymptotic Methods in the Theory of Gaussian Processes and Fields. American Mathematical Society, Providence, RI.Google Scholar
Regnerand, B., Vucinić, D., Domnisoru, C., Bartol, T., Hetzer, M., Tartakovsky, D. and Sejnowski, T. (2013). Anomalous diffusion of single particles in cytoplasm. Biophys. J. 104, 1652–1660.CrossRefGoogle Scholar
Sagi, Y., Brook, M., Almog, I. and Davidson, N. (2012). Observation of anomalous diffusion and fractional self-similarity in one dimension. Phys. Rev. Lett. 108, 093002.10.1103/PhysRevLett.108.093002CrossRefGoogle ScholarPubMed
Talagrand, M. (2014). Upper and Lower Bounds for Stochastic Processes: Modern Methods and Classical Problems. Springer, Heidelberg.CrossRefGoogle Scholar
Taqqu, M., Willinger, W. and Sherman, R. (1997). Proof of a fundamental result in self-similar traffic modeling. Comput. Commun. Rev. 27, 5–23.10.1145/263876.263879CrossRefGoogle Scholar
Winkelbauer, A. (2012). Moments and absolute moments of the normal distribution. Available at arXiv:1209.4340.Google Scholar