Hostname: page-component-cb9f654ff-c75p9 Total loading time: 0 Render date: 2025-08-17T01:44:07.619Z Has data issue: false hasContentIssue false
  • English
  • Français

Asymptotic Probabilities of an Exceedance Over Renewal Thresholds with an Application to Risk Theory

Part of: Stochastic processes Special processes

Published online by Cambridge University Press:  14 July 2016

Christian Y. Robert
Christian Y. Robert*
Affiliation:
CNAM and CREST
*
∗ Postal address: Centre de Recherche en Economie et Statistique, Timbre J320, 15 Boulevard Gabriel Peri, 92245 Malakoff Cedex, France. Email address: chrobert@ensae.fr
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let (Y n , N n )n≥1 be independent and identically distributed bivariate random variables such that the N n are positive with finite mean ν and the Y n have a common heavy-tailed distribution F. We consider the process (Z n )n≥1 defined by Z n = Y n - Σn-1, where 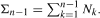It is shown that the probability that the maximum M = maxn≥1 Z n exceeds x is approximately 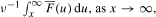as x → ∞, where F' := 1 - F. Then we study the integrated tail of the maximum of a random walk with long-tailed increments and negative drift over the interval [0, σ], defined by some stopping time σ, in the case in which the randomly stopped sum is negative. Finally, an application to risk theory is considered.

Keywords

Renewal processmaximum of a random walkregenerative processstopping timeheavy-tailed distributionruin probabilityrisk theory

MSC classification

Secondary: 60G70: Extreme value theory; extremal processes 60G50: Sums of independent random variables; random walks 60G40: Stopping times; optimal stopping problems; gambling theory 60K30: Applications (congestion, allocation, storage, traffic, etc.)

Information

Type
Research Papers
Information
Journal of Applied Probability , Volume 42 , Issue 1 , March 2005 , pp. 153 - 162
Copyright
© Applied Probability Trust 2005 

References

Asmussen, S. (1987). Applied Probability and Queues. John Wiley, Chichester.Google Scholar
Asmussen, S. (1998). Subexponential asymptotics for stochastic processes: extremal behavior, stationary distributions and first passage probabilities. Ann. Appl. Prob. 8, 354–374.CrossRefGoogle Scholar
Asmussen, S. (2000). Ruin Probabilities (Adv. Ser. Statist. Sci. Appl. Prob. 2). World Scientific, River Edge, NJ.CrossRefGoogle Scholar
Bühlmann, H. (1996). Mathematical Methods of Risk Theory. Springer, Berlin.Google Scholar
Chow, Y. S., Robbins, H. and Teicher, H. (1965). Moments of randomly stopped sums. Ann. Math. Statist. 36, 789–799.CrossRefGoogle Scholar
Embrechts, P. and Veraverbeke, N. (1982). Estimates for the probability of ruin with special emphasis on the possibility of large claims. Insurance Math. Econom. 1, 55–72.CrossRefGoogle Scholar
Feller, W. (1970). An Introduction to Probability Theory and Its Applications, Vol. 1, 3rd edn. John Wiley, New York.Google Scholar
Feller, W. (1971). An Introduction to Probability Theory and Its Applications, Vol. 2, 2nd edn. John Wiley, New York.Google Scholar
Foss, S. and Zachary, S. (2003). The maximum on a random time interval of a random walk with long-tailed increments and negative drift. Ann. Appl. Prob. 13, 37–53.CrossRefGoogle Scholar
Gerber, H.U. (1979). An Introduction to Mathematical Risk Theory (S. S. Huebner Foundation Monogr. Ser. 8). University of Pennsylvania, Philadelphia, PA.Google Scholar
Gut, A. (1974). On the moments and limit distributions of some first passages times. Ann. Prob. 2, 277–306.CrossRefGoogle Scholar
Gut, A. and Janson, S. (1986). Converse results for existence of moments and uniform integrability for stopped random walks. Ann. Prob. 14, 1296–1317.CrossRefGoogle Scholar
Klüppelberg, C. (1988). Subexponential distributions and integrated tails. J. Appl. Prob. 35, 325–347.Google Scholar
Korshunov, D. A. (1997). On distribution tail of the maximum of a random walk. Stoch. Process. Appl. 72, 97–103.CrossRefGoogle Scholar
Veraverbeke, N. (1977). Asymptotic behavior of Wiener–Hopf factors of a random walk. Stoch. Process. Appl. 5, 27–37.CrossRefGoogle Scholar