Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Puterman, Martin L.
1990.
Stochastic Models.
Vol. 2,
Issue. ,
p.
331.
1994.
Markov Decision Processes.
p.
613.
Stidham, Shaler
2000.
Computational Probability.
Vol. 24,
Issue. ,
p.
325.
Yu, Huizhen
and
Bertsekas, Dimitri P.
2015.
A Mixed Value and Policy Iteration Method for Stochastic Control with Universally Measurable Policies.
Mathematics of Operations Research,
Vol. 40,
Issue. 4,
p.
926.

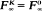 ), determine some of its properties, and relate these to the questions of stability of the process (whether
), determine some of its properties, and relate these to the questions of stability of the process (whether 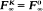 ) and whether a given solution of the dynamic programming equation can be identified with
) and whether a given solution of the dynamic programming equation can be identified with 