Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Belzunce, Félix
and
Shaked, Moshe
2004.
Failure profiles of coherent systems.
Naval Research Logistics (NRL),
Vol. 51,
Issue. 4,
p.
477.
Boland, Philip J.
and
Samaniego, Francisco J.
2004.
Mathematical Reliability: An Expository Perspective.
Vol. 67,
Issue. ,
p.
3.
Navarro, Jorge
Ruiz, Jose M.
and
Sandoval, Carlos J.
2005.
A note on comparisons among coherent systems with dependent components using signatures.
Statistics & Probability Letters,
Vol. 72,
Issue. 2,
p.
179.
Samaniego, Francisco J.
2007.
Encyclopedia of Statistics in Quality and Reliability.
Eryılmaz, Serkan
2010.
Mixture representations for the reliability of consecutive-k systems.
Mathematical and Computer Modelling,
Vol. 51,
Issue. 5-6,
p.
405.
Eryilmaz, Serkan
and
Kan, Cihangir
2010.
Dynamic Reliability Evaluation of Consecutive-k-Within-m-Out-of-n:F System.
Communications in Statistics - Simulation and Computation,
Vol. 40,
Issue. 1,
p.
58.
Li, Shuang
and
Lynch, James
2010.
Some elementary ideas concerning the complexity of system structure.
Naval Research Logistics (NRL),
Vol. 57,
Issue. 7,
p.
626.
Navarro, Jorge
Spizzichino, Fabio
and
Balakrishnan, N.
2010.
Applications of average and projected systems to the study of coherent systems.
Journal of Multivariate Analysis,
Vol. 101,
Issue. 6,
p.
1471.
Eryilmaz, Serkan
2010.
Number of Working Components in Consecutivek-out-of-nSystem While It Is Working.
Communications in Statistics - Simulation and Computation,
Vol. 39,
Issue. 4,
p.
683.
Eryilmaz, Serkan
2010.
Discrete Scan Statistics Generated by Exchangeable Binary Trials.
Journal of Applied Probability,
Vol. 47,
Issue. 04,
p.
1084.
Eryilmaz, Serkan
and
Zuo, Ming J.
2010.
Computing and Applying the Signature of a System With Two Common Failure Criteria.
IEEE Transactions on Reliability,
Vol. 59,
Issue. 3,
p.
576.
Gertsbakh, Ilya
Shpungin, Yoseph
and
Spizzichino, Fabio
2011.
Signatures of Coherent Systems Built with Separate Modules.
Journal of Applied Probability,
Vol. 48,
Issue. 03,
p.
843.
Marichal, Jean-Luc
Mathonet, Pierre
and
Waldhauser, Tamás
2011.
On signature-based expressions of system reliability.
Journal of Multivariate Analysis,
Vol. 102,
Issue. 10,
p.
1410.
Eryilmaz, Serkan
Koutras, Markos V.
and
Triantafyllou, Ioannis S.
2011.
Signature based analysis of m
-Consecutive-k
-out-of-n
: F
systems with exchangeable components.
Naval Research Logistics (NRL),
Vol. 58,
Issue. 4,
p.
344.
Marichal, Jean-Luc
and
Mathonet, Pierre
2011.
Extensions of system signatures to dependent lifetimes: Explicit expressions and interpretations.
Journal of Multivariate Analysis,
Vol. 102,
Issue. 5,
p.
931.
Eryilmaz, Serkan
2011.
The behavior of warm standby components with respect to a coherent system.
Statistics & Probability Letters,
Vol. 81,
Issue. 8,
p.
1319.
Eryılmaz, Serkan
2011.
Circular consecutive k-out-of-n systems with exchangeable dependent components.
Journal of Statistical Planning and Inference,
Vol. 141,
Issue. 2,
p.
725.
Navarro, Jorge
Samaniego, Francisco J.
and
Balakrishnan, N.
2011.
Signature-Based Representations for the Reliability of Systems with Heterogeneous Components.
Journal of Applied Probability,
Vol. 48,
Issue. 03,
p.
856.
Eryilmaz, Serkan
Bayramoglu, Ismihan
and
Pogromsky, Alexander
2012.
On Extreme Residual Lives after the Failure of the System.
Mathematical Problems in Engineering,
Vol. 2012,
Issue. 1,
Eryilmaz, S.
and
Mahmoud, B.
2012.
Linear $m$-Consecutive-$k$, $l$-Out-of-$n$: F System.
IEEE Transactions on Reliability,
Vol. 61,
Issue. 3,
p.
787.
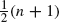 , and use this to show that the expected lifetime of an r × s = n indirect majority system exceeds that of a simple (direct) majority system of size n when the components are exponentially distributed with the same parameter.
, and use this to show that the expected lifetime of an r × s = n indirect majority system exceeds that of a simple (direct) majority system of size n when the components are exponentially distributed with the same parameter.