Article contents
Random affine simplexes
Published online by Cambridge University Press: 12 July 2019
Abstract
For a fixed k ∈ {1, …, d}, consider arbitrary random vectors X0, …, Xk ∈ ℝd such that the (k + 1)-tuples (UX0, …, UXk) have the same distribution for any rotation U. Let A be any nonsingular d × d matrix. We show that the k-dimensional volume of the convex hull of affinely transformed Xi satisfies 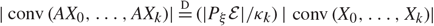 \[|{\rm{conv}}(A{X_{\rm{0}}} \ldots ,A{X_k}){\rm{|}}\mathop {\rm{ = }}\limits^{\rm{D}} (|{P_\xi }\varepsilon |/{\kappa _k})|{\rm{conv}}\left( {{X_0}, \ldots ,{X_k}} \right)\], where ɛ:= {x ∈ ℝd : x┬ (A┬A)−1x ≤ 1} is an ellipsoid, Pξ denotes the orthogonal projection to a uniformly chosen random k-dimensional linear subspace ξ independent of X0, …, Xk, and κk is the volume of the unit k-dimensional ball. As an application, we derive the following integral geometry formula for ellipsoids: ck,d,p∫Ad,k |ɛ ∩ E|p+d+1μd,k(dE) = |ɛ|k+1∫Gd,k |PLɛ|pνd,k(dL), where
\[|{\rm{conv}}(A{X_{\rm{0}}} \ldots ,A{X_k}){\rm{|}}\mathop {\rm{ = }}\limits^{\rm{D}} (|{P_\xi }\varepsilon |/{\kappa _k})|{\rm{conv}}\left( {{X_0}, \ldots ,{X_k}} \right)\], where ɛ:= {x ∈ ℝd : x┬ (A┬A)−1x ≤ 1} is an ellipsoid, Pξ denotes the orthogonal projection to a uniformly chosen random k-dimensional linear subspace ξ independent of X0, …, Xk, and κk is the volume of the unit k-dimensional ball. As an application, we derive the following integral geometry formula for ellipsoids: ck,d,p∫Ad,k |ɛ ∩ E|p+d+1μd,k(dE) = |ɛ|k+1∫Gd,k |PLɛ|pνd,k(dL), where 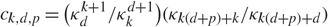 $c_{k,d,p} = \big({\kappa_{d}^{k+1}}/{\kappa_k^{d+1}}\big) ({\kappa_{k(d+p)+k}}/{\kappa_{k(d+p)+d}})$. Here p > −1 and Ad,k and Gd,k are the affine and the linear Grassmannians equipped with their respective Haar measures. The p = 0 case reduces to an affine version of the integral formula of Furstenberg and Tzkoni (1971).
$c_{k,d,p} = \big({\kappa_{d}^{k+1}}/{\kappa_k^{d+1}}\big) ({\kappa_{k(d+p)+k}}/{\kappa_{k(d+p)+d}})$. Here p > −1 and Ad,k and Gd,k are the affine and the linear Grassmannians equipped with their respective Haar measures. The p = 0 case reduces to an affine version of the integral formula of Furstenberg and Tzkoni (1971).
Keywords
Information
- Type
- Research Papers
- Information
- Copyright
- © Applied Probability Trust 2019
References
- 4
- Cited by

