Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Bae, Jongho
Kim, Sunggon
and
Lee, Eui Yong
2003.
Average cost under the PMλ, τ policy in a finite dam with compound Poisson inputs.
Journal of Applied Probability,
Vol. 40,
Issue. 2,
p.
519.
Lim, Kyung Eun
Baek, Jee Seon
and
Lee, Eui Yong
2005.
Optimization under the PMλ,τ policy of a finite dam with both continuous and jumpwise inputs.
Journal of Applied Probability,
Vol. 42,
Issue. 2,
p.
587.
Lim, Kyung Eun
Baek, Jee Seon
and
Lee, Eui Yong
2005.
Optimization under the P
M
λ,τ policy of a finite dam with both continuous and jumpwise inputs.
Journal of Applied Probability,
Vol. 42,
Issue. 02,
p.
587.
Lee, Jiyeon
and
Kim, Jongwoo
2006.
A workload-dependent queue under a two-stage service policy.
Operations Research Letters,
Vol. 34,
Issue. 5,
p.
531.
Abdel-Hameed, M.S.
and
Nakhi, Y.A.
2006.
Optimal control of a finite dam with diffusion input and state dependent release rates.
Computers & Mathematics with Applications,
Vol. 51,
Issue. 2,
p.
317.
Abramov, Vyacheslav M.
2007.
Optimal Control of a Large Dam.
Journal of Applied Probability,
Vol. 44,
Issue. 1,
p.
249.
Abramov, Vyacheslav M.
2007.
Optimal Control of a Large Dam.
Journal of Applied Probability,
Vol. 44,
Issue. 01,
p.
249.
Lämmer, Stefan
and
Helbing, Dirk
2008.
Self-control of traffic lights and vehicle flows in urban road networks.
Journal of Statistical Mechanics: Theory and Experiment,
Vol. 2008,
Issue. 04,
p.
P04019.
Abramov, Vyacheslav M.
2010.
Takács’ Asymptotic Theorem and Its Applications: A Survey.
Acta Applicandae Mathematicae,
Vol. 109,
Issue. 2,
p.
609.
Miller, Boris
and
McInnes, Daniel
2011.
Optimal management of a two dam system via stochastic control: Parallel computing approach.
p.
1417.
Abdel-Hameed, Mohamed
2011.
Control of Dams Using Pλ,τM Policies When the Input Process Is a Nonnegative Lévy Process.
International Journal of Stochastic Analysis,
Vol. 2011,
Issue. ,
p.
1.
Miller, Boris M.
and
McInnes, Daniel J.
2011.
Management of a Large Dam via Optimal Price Control.
IFAC Proceedings Volumes,
Vol. 44,
Issue. 1,
p.
12432.
McInnes, Daniel
and
Miller, Boris
2013.
Optimal control of time-inhomogeneous Markov chains with application to dam management.
p.
230.
Kim, Jongwoo
Song, Mi Jung
and
Lee, Jiyeon
2013.
A two-stage service policy for an M/G/1 queueing system.
Journal of the Korean Data and Information Science Society,
Vol. 24,
Issue. 4,
p.
941.
Abdel-Hameed, Mohamed
2014.
Lévy Processes and Their Applications in Reliability and Storage.
p.
77.
Kim, Sunggon
2018.
Conditional sojourn time distributions in M/G/1 and G/M/1 queues under PλM-service policy.
Communications for Statistical Applications and Methods,
Vol. 25,
Issue. 4,
p.
443.


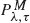 policies assuming that the input process is a compound Poisson process with a non-negative drift term, and using the total discounted cost and long-run average cost criteria. The results of Lee and Ahn (1998) as well as other well-known results are shown to follow from our results.
policies assuming that the input process is a compound Poisson process with a non-negative drift term, and using the total discounted cost and long-run average cost criteria. The results of Lee and Ahn (1998) as well as other well-known results are shown to follow from our results.