Article contents
On the validity of Wald's equation
Published online by Cambridge University Press: 14 July 2016
Abstract
In this paper we review conditions under which Wald's equation holds, mainly if the expectation of the given stopping time is infinite. As a main result we obtain what is probably the weakest possible version of Wald's equation for the case of independent, identically distributed (i.i.d.) random variables. Moreover, we improve a result of Samuel (1967) concerning the existence of stopping times for which the expectation of the stopped sum of the underlying i.i.d. sequence of random variables 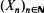 does not exist. Finally, we show by counterexamples that it is impossible to generalize a theorem of Kiefer and Wolfowitz (1956) relating the moments of the supremum of a random walk
does not exist. Finally, we show by counterexamples that it is impossible to generalize a theorem of Kiefer and Wolfowitz (1956) relating the moments of the supremum of a random walk  with negative drift to moments of the positive part of X 1 to the case where the expectation of X 1 is —∞. Here, the Laplace–Stieltjes transform of the supremum of the considered random walk plays an important role.
with negative drift to moments of the positive part of X 1 to the case where the expectation of X 1 is —∞. Here, the Laplace–Stieltjes transform of the supremum of the considered random walk plays an important role.
Keywords
MSC classification
Information
- Type
- Research Article
- Information
- Copyright
- Copyright © Applied Probability Trust 1994
References
- 9
- Cited by

