Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Hering, H.
1978.
The non-degenerate limit for supercritical branching diffusions.
Duke Mathematical Journal,
Vol. 45,
Issue. 3,
Pakes, Anthony G.
1979.
Limit theorems for the simple branching process allowing immigration, I. The case of finite offspring mean.
Advances in Applied Probability,
Vol. 11,
Issue. 1,
p.
31.
Pakes, Anthony G.
1979.
Limit theorems for the simple branching process allowing immigration, I. The case of finite offspring mean.
Advances in Applied Probability,
Vol. 11,
Issue. 1,
p.
31.
2010.
Introduction to Stochastic Models.
p.
343.
Foucart, Clément
Ma, Chunhua
and
Yuan, Linglong
2022.
Limit theorems for continuous-state branching processes with immigration.
Advances in Applied Probability,
Vol. 54,
Issue. 2,
p.
599.

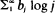 of the immigration distribution is infinite, then no sequence of positive constants {
of the immigration distribution is infinite, then no sequence of positive constants {