Hostname: page-component-745bb68f8f-hvd4g Total loading time: 0 Render date: 2025-01-11T02:56:31.456Z Has data issue: false hasContentIssue false
  • English
  • Français

The number of K-tons in the coupon collector problem

Part of: Distribution theory - Probability Combinatorial probability

Published online by Cambridge University Press:  07 February 2023

John C. Saunders Open the ORCID record for John C. Saunders [Opens in a new window]
John C. Saunders*
Affiliation:
Middle Tennessee State University
*
*Postal address: Middle Tennessee State University Department of Mathematical Sciences. Email: John.Saunders@mtsu.edu
Get access Rights & Permissions [Opens in a new window]

Abstract

Consider the coupon collector problem where each box of a brand of cereal contains a coupon and there are n different types of coupons. Suppose that the probability of a box containing a coupon of a specific type is 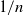$1/n$, and that we keep buying boxes until we collect at least m coupons of each type. For 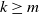$k\geq m$ call a certain coupon a k-ton if we see it k times by the time we have seen m copies of all of the coupons. Here we determine the asymptotic distribution of the number of k-tons after we have collected m copies of each coupon for any k in a restricted range, given any fixed m. We also determine the asymptotic joint probability distribution over such values of k, and the total number of coupons collected.

Keywords

Probability distributionscombinatorial probability

MSC classification

Primary: 60E05: Distributions
Secondary: 60C05: Combinatorial probability
Type
Original Article
Information
Journal of Applied Probability , Volume 60 , Issue 3 , September 2023 , pp. 723 - 736
Check for updates
Copyright
© The Author(s), 2023. Published by Cambridge University Press on behalf of Applied Probability Trust

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Baum, L. and Billingsley, P. (1965). Asymptotic distributions for the coupon collector’s problem. Ann. Math. Statist. 36, 1835–1839.CrossRefGoogle Scholar
Berenbrink, P. and Sauerwald, T. (2009). The weighted coupon collector’s problem and applications. In Computing and Combinatorics (LNCS 5609), ed H. Q. Ngo. Springer, Berlin, pp. 449–458.CrossRefGoogle Scholar
Doumas, A. and Papanicolaou, V. (2012). The coupon collector’s problem revisited: Asymptotics of the variance. Adv. Appl. Prob. 44, 166–195.CrossRefGoogle Scholar
Doumas, A. and Papanicolaou, V. (2016). The coupon collector’s problem revisited: Generalizing the double Dixie cup problem of Newman and Shepp. ESIAM Prob. Statist. 20, 367–399.CrossRefGoogle Scholar
Erdös, P. and Rényi, A. (1961). On a classical problem of probability theory. Magyar Tudományos Akadémia Matematikai Kutató Intézetének Közleményei 6, 215–220.Google Scholar
Foata, D. and Han, G. (2001). Les nombres hyperharmoniques et la fratrie du collectionneur de vignettes. Séminaire Lotharingien de Combinatoire 47, B47a.Google Scholar
Myers, A. and Wilf, H. (2006). Some new aspects of the coupon collector’s problem. SIAM Rev. 48, 549–565.10.1137/060654438CrossRefGoogle Scholar
Neal, P. (2008). The generalised coupon collector problem. J. Appl. Prob. 45, 621–629.CrossRefGoogle Scholar
Newman, D. and Shepp, L. (1960). The double Dixie cup problem. Amer. Math. Monthly 67, 58–61.10.2307/2308930CrossRefGoogle Scholar
Penrose, M. (2009). Normal approximation for isolated balls in an urn allocation model. Electron. J. Prob. 14, 2155–2181.CrossRefGoogle Scholar