Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Ball, Frank
1990.
Stochastic Processes in Epidemic Theory.
Vol. 86,
Issue. ,
p.
71.

 as the initial number of susceptibles tends to infinity. Here ρ denotes the relative removal rate for carriers,
as the initial number of susceptibles tends to infinity. Here ρ denotes the relative removal rate for carriers, 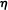 denotes the initial number of carriers.
denotes the initial number of carriers.