Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Mikosch, T.
1997.
Heavy-tailed modelling in insurance.
Communications in Statistics. Stochastic Models,
Vol. 13,
Issue. 4,
p.
799.
Nyrhinen, Harri
1998.
Rough descriptions of ruin for a general class of surplus processes.
Advances in Applied Probability,
Vol. 30,
Issue. 4,
p.
1008.
Christensen, Claus Vorm
and
Schmidli, Hanspeter
2000.
Pricing catastrophe insurance products based on actually reported claims.
Insurance: Mathematics and Economics,
Vol. 27,
Issue. 2,
p.
189.
Su, Chun
Tang, Qihe
and
Jiang, Tao
2001.
A contribution to large deviations for heavy-tailed random sums.
Science in China Series A: Mathematics,
Vol. 44,
Issue. 4,
p.
438.
Tang, Qihe
and
Yan, Jia’an
2002.
A sharp inequality for the tail probabilities of sums of i.i.d. r.v.’s with dominatedly varying tails.
Science in China Series A: Mathematics,
Vol. 45,
Issue. 8,
p.
1006.
Muermann, Alexander
2002.
Pricing Catastrophe Insurance Derivatives.
SSRN Electronic Journal ,
Paulauskas, V.
and
Skučaitė, A.
2003.
Some Asymptotic Results for One-Sided Large Deviation Probabilities.
Lithuanian Mathematical Journal,
Vol. 43,
Issue. 3,
p.
318.
Wang, Han-xing
Fang, Da-fan
and
Tang, Mao-ning
2003.
Ruin Probabilities under a Markovian Risk Model.
Acta Mathematicae Applicatae Sinica, English Series,
Vol. 19,
Issue. 4,
p.
621.
Liu, Yan
and
Hu, Yijun
2003.
Large deviations for heavy-tailed random sums of independent random variables with dominatedly varying tails.
Science China Mathematics,
Vol. 46,
Issue. 3,
p.
383.
Cai, Jun
2004.
Encyclopedia of Actuarial Science.
Jelenković, Predrag R.
and
Momčilović, Petar
2004.
Large Deviations of Square Root Insensitive Random Sums.
Mathematics of Operations Research,
Vol. 29,
Issue. 2,
p.
398.
Tang, Qihe
and
Tsitsiashvili, Gurami
2004.
Finite- and infinite-time ruin probabilities in the presence of stochastic returns on investments.
Advances in Applied Probability,
Vol. 36,
Issue. 4,
p.
1278.
Skučaitė, A.
2004.
Large Deviations for Sums of Independent Heavy-Tailed Random Variables.
Lithuanian Mathematical Journal,
Vol. 44,
Issue. 2,
p.
198.
Klüppelberg, Claudia
2004.
Encyclopedia of Actuarial Science.
Tang, Qihe
2004.
UNIFORM ESTIMATES FOR THE TAIL PROBABILITY OF MAXIMA OVER FINITE
HORIZONS WITH SUBEXPONENTIAL TAILS.
Probability in the Engineering and Informational Sciences,
Vol. 18,
Issue. 1,
p.
71.
Cai, Jun
2004.
Encyclopedia of Actuarial Science.
Ng, Kai W.
Tang, Qihe
Yan, Jia-An
and
Yang, Hailiang
2004.
Precise large deviations for sums of random variables with consistently varying tails.
Journal of Applied Probability,
Vol. 41,
Issue. 01,
p.
93.
Kaas, Rob
and
Tang, Qihe
2005.
A large deviation result for aggregate claims with dependent claim occurrences.
Insurance: Mathematics and Economics,
Vol. 36,
Issue. 3,
p.
251.
Hu, Yi Jun
2005.
Finite Time Ruin Probabilities and Large Deviations for Generalized Compound Binomial Risk Models.
Acta Mathematica Sinica, English Series,
Vol. 21,
Issue. 5,
p.
1099.
Wang, Yue Bao
Wang, Kai Yong
and
Cheng, Dong Ya
2006.
Precise Large Deviations for Sums of Negatively Associated Random Variables with Common Dominatedly Varying Tails.
Acta Mathematica Sinica, English Series,
Vol. 22,
Issue. 6,
p.
1725.

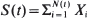 ,
, 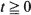 , where
, where 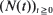 are non-negative integer-valued random variables and are
are non-negative integer-valued random variables and are 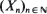 i.i.d. non-negative random variables with common distribution function
i.i.d. non-negative random variables with common distribution function 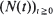 . Special attention is paid to the compound Poisson process and its ramifications. The right tail of the distribution function
. Special attention is paid to the compound Poisson process and its ramifications. The right tail of the distribution function 