Article contents
Generalized adaptive exponential smoothing procedures
Published online by Cambridge University Press: 14 July 2016
Abstract
The classical exponential smoothing procedure to be applied to a sequence of observations 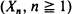 is modified into some adaptive variants and also generalized to the recursive scheme
is modified into some adaptive variants and also generalized to the recursive scheme
This means that given the history of observations and smoothed values up to time n, the updated smoothed value Wn + 1 is given by a function u of Wn and Xn , which satisfies only certain structural properties. We study these procedures within the framework of random systems with complete connections and exploit results from Markov process theory to study the sequence 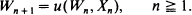 . A broad class of ‘smoothing functions' u, which induce sequences
. A broad class of ‘smoothing functions' u, which induce sequences 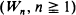 with nice statistical properties, is presented. A method to estimate the limit of the expected smoothed values is also developed.,
with nice statistical properties, is presented. A method to estimate the limit of the expected smoothed values is also developed.,
Keywords
Information
- Type
- Research Papers
- Information
- Copyright
- Copyright © Applied Probability Trust 1994
References
- 5
- Cited by

