Hostname: page-component-cb9f654ff-qc88w Total loading time: 0 Render date: 2025-08-21T14:47:46.032Z Has data issue: false hasContentIssue false
  • English
  • Français

Denumerable Markov processes with bounded generators: a routine for calculating pij (∞)

Published online by Cambridge University Press:  14 July 2016

Arne Jensen  and
David Kendall
Arne Jensen
Affiliation:
University of Copenhagen
David Kendall
Affiliation:
University of Cambridge
Get access Rights & Permissions [Opens in a new window]

Extract

1. Let the (honest) Markov process with transition functions (pij (0)) have transition rates (qij ) and suppose that, for some M,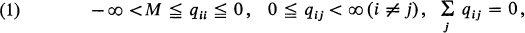 so that the matrix Q = (qij ) determines a bounded operator on the Banach space l 1 by right-multiplication. Then in the terminology of [8], (pp. 12 and 19) Q will be bounded and ΩF will be a closed restriction of Q with dense domain, so that ΩF = Q; that is, we shall have a process whose associated semigroup has a bounded generator. In these circumstances Theorem 10.3.2 of [2] applies and the matrix Pt = (pij (t)) is given by 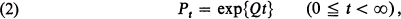where exp{·} denotes the function defined by the exponential power-series. We shall be interested here (as in [5] and [9]) in the determination of the limit matrix P ∞ = (limt→∞ pij (t)).

Information

Type
Short Communications
Information
Journal of Applied Probability , Volume 8 , Issue 2 , June 1971 , pp. 423 - 427
Copyright
Copyright © Applied Probability Trust 1971 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Article purchase

Temporarily unavailable

References

[1] Hardy, G. H. (1949) Divergent Series. Oxford University Press.Google Scholar
[2] Hille, E. and Phillips, R. S. (1957) Functional Analysis and Semigroups. American Mathematical Society.Google Scholar
[3] Jensen, A. (1953) Markov chains as an aid in the study of Markov processes. Skand. Aktuartidskr. 36, 87–91.Google Scholar
[4] Jensen, A. (1954) A Distribution Model Applicable to Economics. Munksgaard, Copenhagen.Google Scholar
[5] Kendall, D. G. and Reuter, G. E. H. (1957) The calculation of the ergodic projection for Markov chains and processes with a countable infinity of states. Acta. Math. 97, 103–144.Google Scholar
[6] Kerridge, D. Personal communication.Google Scholar
[7] Kingman, J. F. C. (1961) Two similar queues in parallel. Ann. Math. Statist. 32, 1314–1323.Google Scholar
[8] Reuter, G. E. H. (1957) Denumerable Markov processes and the associated contraction semigroups on l1. Acta. Math. 97, 1–46.Google Scholar
[9] Vere-Jones, D. and Kendall, D. G. (1959) A commutativity problem in the theory of Markov chains. Theor. Probability Appl. 4, 92–95.Google Scholar