Article contents
An optimal sequential policy for controlling a Markov renewal process
Published online by Cambridge University Press: 14 July 2016
Abstract
This paper discusses a renewal process whose time development between renewals is described by a Markov process. The process may be controlled by choosing the times at which renewal occurs, the objective of the control being to maximise the long-term average rate of reward. Let γ ∗ denote the maximum achievable rate. We consider a specific policy in which a sequence of estimates 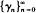 of γ ∗ is made. This sequence is defined inductively as follows. Initially an (a priori)estimate γo is chosen. On making the nth renewal one estimates γ ∗ in terms of γo, the total rewards obtained in the first n renewal cycles and the total length of these cycles. γ n then determines the length of the (n + 1)th cycle. It is shown that γ n tends to γ ∗ as n tends to∞, and that this policy is optimal.
of γ ∗ is made. This sequence is defined inductively as follows. Initially an (a priori)estimate γo is chosen. On making the nth renewal one estimates γ ∗ in terms of γo, the total rewards obtained in the first n renewal cycles and the total length of these cycles. γ n then determines the length of the (n + 1)th cycle. It is shown that γ n tends to γ ∗ as n tends to∞, and that this policy is optimal.
The time at which the (n + 1)th renewal is made is determined by solving a stopping problem for the Markov process with continuation cost γ n per unit time and stopping reward equal to the renewal reward. Thus, in general, implementation of this policy requires a knowledge of the transition probabilities of the Markov process. An example is presented in which one needs to know essentially nothing about the details of this process or the fine details of the reward structure in order to implement the policy. The example is based on a problem in biology.
Information
- Type
- Research Papers
- Information
- Copyright
- Copyright © Applied Probability Trust 1985
References
- 8
- Cited by

