INTRODUCTION
I was asked to mark this 40th meeting by presenting a brief history of the Agricultural Research Modellers Group from its formation to the present day, outlining along the way the scientific and political changes that have helped shape it. Such a task is rarely easy and the end product is never completely accurate (you have to rely on incomplete records, old notes and the recollections of people whose memories go back further than your own). Yet it is a worthwhile exercise. Knowing where we come from helps us to know where we are going, or to quote Sir Winston Churchill in 1945: ‘the longer you can look back, the farther you can look forward’. For the record and for the pedantically inclined, this is not the 40th annual meeting of our group, but the 40th meeting. Two meetings were held in both 1993 and 1995.
PREVIOUS MEETINGS
The group was founded by our present chairman John Thornley in 1970. One of John's initiatives on joining the then Agricultural Research Council (ARC) in May 1969 to head the newly created Biomathematics Department at the Glasshouse Crops Research Institute (GCRI) in Littlehampton, West Sussex was to form a network of ARC crop science modellers. This resulted in the first meeting of the Crop Science Model Builders Working Party, as the Agricultural Research Modellers Group was originally known, being held on the 2 April 1971 at ARC Headquarters, 160 Great Portland Street, London. There were six speakers, including John who spoke about plant respiration or dry matter partitioning (a copy of the actual programme no longer exists) and Gavin Ross from Rothamsted Experimental Station (RES) at Harpenden who described early developments in the statistical software GENSTAT. The meeting was chaired by Dennis Cooke of the University of Sussex and 30 people attended. It was deemed a success.
Following this successful first meeting, a second meeting of the group was held at the same venue on 24 March 1972. Dick Brockington from the Grassland Research Institute (GRI) at Hurley chaired and 54 people attended. Nine presentations were made, including one by Peter Nye (University of Oxford) and Duncan Greenwood (National Vegetable Research Station, NVRS) on a model for predicting the response of cabbage to fertilizers in the field, and one by John on a model of a biochemical switch and its possible application to flower initiation. Among those who attended was a young soil scientist from RES, Derek Rose, who subsequently joined GCRI and organized many of the early meetings and has been a regular attendee to this day.
In 1973, the group was renamed the Crop Science Model Builders Group to reflect that it and its annual meetings were now a permanent feature. The venue was moved from ARC Headquarters to the Royal Society, the present venue, for the fifth meeting which was held on 18 March 1975; every meeting since, bar one, has been held here. The fifth meeting was chaired by Duncan Greenwood, later awarded his FRS, and of the eight talks which were presented, one was given by Gavin Ross on properties of polynomials and the logistic family of growth curves, and one by John Thornley on a field theory of phyllotaxis. The meeting was also the first attended by another ‘regular’, Eric Audsley of the National Institute of Agricultural Engineering at Silsoe.
Prior to the seventh meeting the group underwent another name change, incorporating the acronym ARC and becoming the ARC Crop Science Model Builders Group. The seventh meeting, held on 1 April 1977 and chaired by Harold Woolhouse of the John Innes Institute, Norwich, also marks another milestone. Rudy Rabbinge travelled from Wageningen to present a talk entitled ‘The Basis of Models of Crop Growth’, thus becoming the first overseas delegate to address our group. John Monteith of the University of Nottingham, later awarded his FRS, also spoke at the meeting, describing a model of condensation induced by thermal lag, with special reference to cacao pods.
To mark the group's tenth birthday, the tenth meeting took the form of a 2-day symposium on quantitative aspects of plant physiology. It was held on the 27–28 March 1980, not at AFRC Headquarters but in Bewley Hall at the GCRI, and organized in four sessions: I. Processes at the Cell Level, II. Processes at the Organ Level, III. Processes at the Crop Level: Productivity in Relation to Environment, and IV. Techniques for Modelling. Talks given included the mathematical description of control processes by David Charles-Edwards (GCRI) in session I, organogenesis by John Thornley and gas exchange in leaves by Derek Rose in session II, crop models and agronomic practices by Duncan Greenwood in session III, and the use of non-linear regression methods by Gavin Ross in session IV. John Monteith chaired session III and John Thornley chaired session IV. Proceedings of the meeting were published as a book (Rose & Charles-Edwards Reference Rose and Charles-Edwards1981), and the monograph still endures.
My involvement with the group began when I attend the 11th meeting, held on 10 April 1981 and chaired by Terry Woodhead (RES), to present a talk on modelling grazed grassland systems. The model which I described was in fact an animal model (a bio-energetic sheep growth model), but it did contain a rudimentary empirical pasture growth routine and thus just about qualified for the programme! This seemed to set a precedent and the group was reformed in 1982 at John Thornley's instigation (John had moved from GCRI in 1980 to head the Biomathematics Division at GRI and had expanded his modelling interests) to become the ARC Modellers Group, its scope extended to cover animal science, engineering and other aspects of agriculture as well as crop science. The first three talks at the 12th meeting, chaired by the late David Aikman (GCRI) and held on 2 April 1982, were a model of the rumen by myself (then at GRI), a model of animal growth and feed intake on ad libitum feeding by Gerry Emmans of the then East of Scotland College of Agriculture, and selecting the size of tractor for tillage using dynamic programming by Eric Audsley, reflecting this broader scope.
In 1986, the ARC became the Agricultural and Food Research Council (AFRC), reflecting the increasing attention given to matters of food quality by the general public (and therefore by the government), and our group became the AFRC Modellers Group. In 1994, the AFRC morphed into the present Biotechnology and Biological Sciences Research Council (BBSRC), reflecting the government's move away from traditional agricultural research towards molecular biology, and the AFRC Modellers' Group changed its name to the Agricultural Research Modellers' Group. The BBSRC acronym was not included in the new name due, among other things, to their curt rejection of my requests for financial sponsorship!
To mark the 20th anniversary of the group, I arranged with the late Sir Kenneth Blaxter FRS, then a senior editor at the Journal of Agricultural Science, Cambridge, for his journal to publish abstracts of the talks to be given at the 20th meeting (Sir Kenneth had previously chaired the 17th meeting, 10 April 1987). The 20th meeting was held on 6 April 1990 and chaired by John MacRae of the Rowett Research Institute (RRI), and the proceedings duly published later that year (France Reference France1990). Proceedings of each meeting have been carried as abstracts by the Journal ever since. A recent innovation has been to include the full text of any occasional plenary paper in the proceedings. The first plenary lecture that appeared in this way was fittingly given by John Thornley to the 38th meeting (Thornley Reference Thornley2006), held 2 years ago on 31 March 2006 and chaired by Amir Kassam of the University of Reading.
The organization of the meeting was originally based at the GCRI in Littlehampton. John organized the first six meetings, before handing over to David Charles-Edwards for the seventh and eighth meetings. Derek Rose then organized the next seven meetings, helped by David and Andrew Picken initially. When Derek left GCRI for the University of Newcastle-upon-Tyne in the mid-1980s, the organization came to the GRI at Hurley where John Thornley had taken up a senior position as previously mentioned. John decreed that I now take responsibility for the group and run the meetings. So I organized the next 21 (the 16th to the 36th meeting), initially with David Sweeney and latterly with Les Crompton. The organization left GRI (subsequently renamed the Institute for Grassland and Environmental Research, IGER) and came to the University of Reading, where it remains, when I took up a chair there in 1997. I left Reading for Canada in 2003, leaving Les Crompton and Tim Wheeler in joint charge of arrangements since 2004. It is interesting to note that GRI underwent four name changes in just a short space of time in the mid-1980s: GRI to Animal and Grassland Research Institute, then Institute of Grassland and Animal Production, and finally IGER. Clearly this was a period of great change in the agricultural research service and agricultural research generally. I shall address these changes in the next section.
A CHANGING CLIMATE
I will illustrate change with reference to animal agriculture, as this is what I am familiar with. From 1945 to the early 1970s the political driver of UK animal agriculture was increasing animal production, to alleviate food shortages after World War II. This was highly successful as food rationing stopped in the 1950s and shortages had been virtually eliminated by the 1960s. From the early 1970s to the mid-1980s the emphasis was on increasing productive efficiency, the success of which led to butter, milk and meat ‘mountains’ in Europe. In the mid-1980s emphasis changed to improving product quality, mainly to satisfy consumer perception for high protein and low fat products, by which time food shortages had become a distant memory to the consumer. Since the beginning of the new millennium, we no longer talk about animal (or crop) production, but about sustainable agriculture, the political drivers of which have been environmental issues such as countryside management and greenhouse gas and nitrogen pollution from livestock systems. There are now indications that this is changing, as consumer rather than environmental issues begin to dominate sustainable agriculture, issues such as animal products for the health-conscious consumer and the economics of sustainable markets (beyond subsidies). Coupled with these political changes have been revolutionary advances in molecular biology and the birth of biotechnology in the 1980s.
This political change and revolutionary scientific advance has had a dramatic effect on traditional agricultural research, resulting in major downsizing as the new and appealing environmental and molecular sciences compete for limited government resources. We have seen the ARC morph into the AFRC and then into the present BBSRC. When our group first met on that sunny day in April 1971 there were 29 research organizations under the aegis of the ARC (Table 1). Many world famous names are long gone, such as the Letcombe Laboratory, the National Institute for Research in Dairying, not to mention NVRS and GCRI. Today, the BBSRC and the Scottish Executive Environment and Rural Affairs Department (SEERAD) support seven and five institutes respectively (Table 2), and several of these are scheduled for closure. IGER is in the process of merging with RES and the University of Aberystwyth, the RRI with the University of Aberdeen, and the Macaulay Institute is in merger discussions with the Scottish Crops Research Institute. Also the future of the Hannah Research Institute looks uncertain. The picture is similar in the universities. There were 11 Departments of Agriculture in British universities in 1971, all of which were highly research-active (Table 3). Only four pre-1992 universities now boast a Department of Agriculture and agricultural science is no longer taught at the Universities of Oxford, Cambridge or Edinburgh for example (Table 3). So what of the future of the Agricultural Research Modellers' Group? Is it terminal decline? I think not. There are reasons for optimism.
Table 1. Organizations co-ordinated by the Agricultural Research Council in 1971

Table 2. Agricultural Research Organizations supported by BBSRC and SEERAD in 2008

Table 3. Departments of Agriculture in British Universities

a Designated for closure around this time.
A FORWARD LOOK
Agriculture contributes over £5 billion a year to the UK economy and accounts as a proportion for 0·005 of gross domestic product (GDP). It is a significant industry vital to the rural way of life. In terms of the annual UK balance of trade, we import a staggering £13·5 billion's worth of food more than we export (Table 4). We import 11 times more fruit and vegetables, 5 times more meat, 2·5 times more dairy produce and twice as much fish than we sell overseas (Table 5). Given the importance of agriculture to the British economy, and the vulnerability of our food supply to world oil prices and world food shortages, it is reasonable to suppose that any sensible government (and whether we like them or not, governments tend to be both rational and intelligent) will support a broad-based infrastructure capable of delivering high-quality agricultural research. Our group should prosper whilst UK agricultural research has the support of its government.
Table 5. Balance of UK agricultural trade by sectorFootnote a
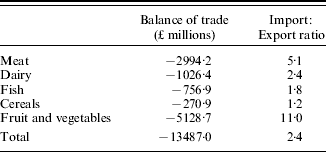
a Source: UK Agriculture Statistics (2005).
Another reason for optimism is that the opportunities for modelling have never been greater, and there are a number of reasons for this. First, Government's increasing pre-occupation with consumer and environmental issues fuels the need for mathematical modelling, the need for good process-based simulation models for example. Many of the issues simply cannot be addressed without such tools. Second, computer software and hardware are forever improving in terms of their affordability, flexibility and quality. Just pause for a moment to consider the computing that was available to us in 1971 and what is available now. Third, opportunities to mine and manipulate data have never been greater. As a consequence of the advances in computing and instrumentation, data are being generated in the traditional (‘old’) areas of agricultural research at a rapidly increasing rate. But as the climate within which traditional agricultural science operates has become increasingly turbulent, academics and researchers are taking early retirement, those in mid career are changing occupations, and there is a higher turnover amongst young postdoctoral workers. Consequently, each unit of data generated now receives less attention from the experimentalist than would have been the case in past years, providing opportunity for the agricultural modeller. Fourth, the development of high-throughput techniques in the ‘-omics’ research areas (genomics, proteomics and metabolomics) is producing large quantities of data at the molecular level. These ‘new’ data are extensive but also expensive, and how to make best use of them is becoming a pressing problem (Thornley Reference Thornley2006). This clearly provides an opportunity for modellers wishing to operate mechanistically at the cellular and sub-cellular organizational levels. Given the opportunities that exist for mining and synthesizing both ‘old’ and ‘new’ data, there is a case for funding proportionately more dry (in silico) and proportionately less wet (in vitro, in vivo) biological research in future. And finally, modelling is now de rigueur in agriculture and applied biology generally, to quote Thornley (Reference Thornley2006). Not only is it an expected requirement for research programmes that aim to understand the responses of complex agricultural systems, it is encouraged. This means that winning research grants and publishing papers is relatively easier than it was even a decade ago.
How is our group weathering the storms of change? Quite well appears to be the answer. Numbers attending the first 40 meetings are plotted in Fig. 1. These show a linear increase from 30 to 85 between 1971 and 1980, followed by a linear decline until 1986, since when numbers have remained fairly static at around 40. This is pretty remarkable and highly encouraging given how many agricultural research institutes and university departments have closed since the mid-1980s.
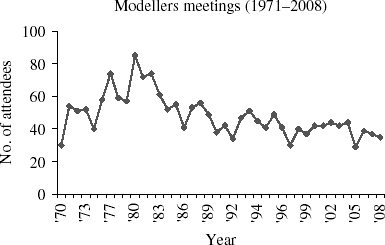
Fig. 1. Numbers attending the first 40 meetings.
So there are a number of good reasons for optimism about the future, yet none for complacency. What can we do to be pro-active and maintain or increase numbers? A few things come to mind. First, invite a broad range of external speakers. Invitations could be given not only to scientists but also to politicians, senior administrators and opinion leaders. Why not for example invite Prince Charles to speak? After all, HRH has much to say about agriculture. Second, extend the scope of the meetings to encompass the environmental and food sciences. There is a precedent for this. Back in 1982 the scope of the meetings was successfully broadened to cover animal science and other aspects of agriculture in addition to crop science. This extension would be logical given the government's current focus on environmental and consumer issues in agriculture. Third, vary the format of meetings. A highly successful 2-day meeting, where 85 people attended, was held in 1980 to mark the tenth anniversary of the group. Why not repeat the formula to mark the 50th meeting in 10 years' time? International scientists could be invited to speak and asked to present major reviews for subsequent publication, using Rose & Charles-Edwards (Reference Rose and Charles-Edwards1981) as an exemplar. Fourth, more actively encourage PhD students and postdoctoral fellows to present. Many of us here today train highly qualified personnel. Why do we not oblige them to prepare an abstract and present at this meeting as part of their training? These are just a few things that come to mind. Other people will have other suggestions. So the Group might consider setting up an informal sub-group to explore these and other ideas.
CONCLUSIONS
The meetings of the Agricultural Research Modellers' Group, which has endured a difficult research climate over the last 25 years, have a modest but continuing appeal. The Group appears to have found a niche. Despite this, complacency must be avoided and the Group must look forward by clearly defining the challenges facing the modelling community in agriculture, then aligning its focus appropriately.
The growth of trees and other plants occurs through the interactive combinations of photosynthesis and carbon (and other nutrient) storage. Photosynthesis enables the production of carbohydrate which can then be used in growing foliage, whereby photosynthesis is further enhanced due to increased leaf surface area. A mathematical model of carbon assimilation and storage was constructed which allows prediction of the growth dynamics of trees. It was found that the simplest model allows uncontrolled foliage production through the positive feedback outlined above, but that leaf shading provides an automatic saturation to carbon assimilation and hence to foliage production. The model was able to predict many observed features of plant growth such as saturation of leaf growth and temporal carbon storage dynamics within the growing season. In particular, it was found that the model provides a descriptive reason why at budbreak, leaves form with a small but finite capacity for photosynthesis. In addition, it was shown that leaf shading provides a practical mechanism by which foliage growth is limited and the carbon storage reaches a steady state. Both of these features provide insight into the mechanisms of carbon regulation during tree growth.
This model finds its origins in the pioneering work of Thornley (Reference Thornley1976) and indeed it closely resembled the whole plant model developed by Thornley for tomato plants. However, it went beyond Thornley's model in two respects. The first is that an a priori derivation of the model equations from first principles were given, describing the processes of water and nutrient transport within the tree and secondly the model was analysed and showed that in its simplest form it exhibits an unphysical indefinite growth of foliage. Later the effects of leaf shading were included and showed that the resultant augmented model allows for growth to a stable steady state, consistent with annual foliage development in mature trees.
During the development of mechanistic models judgements must be made about the appropriate level of detail for modelled processes. These judgements are difficult to test, with the validity of a model normally being assessed holistically by comparisons between predictions and observations. While sensitivity and uncertainty analysis can play a useful role they do not usually test the sensitivity of a model to its structure, or the uncertainty in predictions due to uncertainty in model formulation. The work described is a step towards addressing these difficulties.
A method which reduced a model to a family of alternative combinations by replacing model variables with constants (Model Reduction by Variable Replacement) was proposed and implemented. The procedure iteratively searches the alternative model formulations and compares models in terms of their ability to predict observed data, evaluated within a Bayesian framework. The results can be summarized as posterior model probabilities and replacement probabilities for individual variables which lend themselves to mechanistic interpretation. This provides powerful diagnostic information to support model development. The application of the method to the SIRIUS wheat model is presented, identifying reduced models which outperform the original full model in terms of comparisons to observations. Modelled processes that are replaced relate to (i) calculation of canopy temperature, (ii) diurnal temperature variation, (iii) vernalization, and (iv) soil nitrogen supply and physiology. It is argued that the proposed approach is relevant to anyone involved in the development or use of process based mathematical models, especially those where understanding is encoded via empirically based relationships.
Environmental life cycle assessment (LCA) is used to calculate the burdens of producing food commodities to a common point, typically the farm gate, to yield life cycle inventories (LCI). Once achieved and hotspots are identified, a normal reaction is to seek to reduce environmental burdens by changing a system or comparing alternatives. This paper shows how systems modelling can be used to facilitate such comparisons for wheat and milk production and so aid sound decision-making.
A conventional LCA calculates all the resources used and emissions to the environment involved in producing a unit of commodity, e.g. 1 kg bread wheat or 1 litre milk. A simple approach is to take data values as constants, which enables the LCA to be completed and for hotspots to be identified, but does not permit changes in the production system to be analysed adequately.
The Cranfield LCA approach (www.agrilca.org) uses models of systems and process to account for changes and link components. Wheat yield is calculated from N supply using a long-term response curve, based on long term experiments at Rothamsted's Broadbalk plots (Fig. 1) in which N inputs and outputs and balanced. The difference between N supply and offtake is surplus N that is partitioned into leaching and denitrification as a function of crop yield, soil texture and rainfall. This approach does not allow soil N to be arbitrarily depleted. Machinery inputs (both diesel use and manufacturing energy) are correlated to soil texture or/or yield.
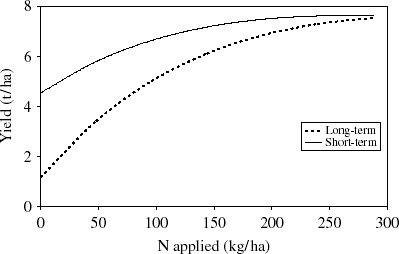
Fig. 1. Long- and short-term yield response curves for bread wheat.
In milk production, a cow's milk yield interacts with energy and protein requirements, enteric methane emissions, manure production, N excretion and cow size. These are modelled together with characteristics such as lactation number and length and calving timing. The forage type determines concentrate characteristics, which are met from crops and crop by-products for which LCIs have been calculated using models like those for wheat, together with transport and processing needs.
Scenarios have been examined with systems models. With non-organic bread wheat, there is a minimum for energy use and greenhouse gas emissions (GHG) at about 0·50 and 0·70 of current national N fertilizer application rates, but yields and grain protein concentrations fall, so requiring more land (1·2 and 2·2 times more respectively) per unit mass. Increasing milk yields per cow from 5800 to 7800 l/lactation reduces energy and GHG emissions/litre by about 10%. This includes assumptions about breed substitution, but the key factor is the efficiency of converting feed energy in milk as the production phase dominates all. In wheat production, N utilization efficiency is a dominant factor.
We gratefully acknowledge funding from UK DEFRA.
The heterogeneity of the pore space of soil has long been recognized (Lawes et al. Reference Lawes, Gilbert and Warington1881). The main intellectual approach to this heterogeneity of structure is to construct a dual porosity model of the soil: structural units containing micropores are separated by macropores through which fluids can move freely, the fluid in the micropores remaining effectively stagnant. Solutes within the system move in two ways, through the macropores (the mobile-water region) by convection and hydrodynamic dispersion, and through the micropores (the immobile-water region) by diffusion alone. This approach is termed the mobile–immobile model (van Genuchten & Wierenga Reference van Genuchten and Wierenga1976).
This model was tested by performing experiments in which the solutions in the macropores and micropores of inert spheroids were separately labelled. There were eight leaching experiments in a 2×2×2 combination in which (i) the macropores and micropores were filled with monovalent (KBr) and divalent (CaSO4) solutions respectively, or vice versa, (ii) the flow was continuous or interrupted; (iii) themacropores remained saturated or were periodically drained. Breakthrough curves of Br−, K+, Ca2+ and SO42− in the effluent were measured and cumulative leaching losses of these ions were calculated. These data were compared with predictions from the transport model of longitudinal hydrodynamic dispersion in the macropores coupled with radial diffusion in the micropores (van Beinum Reference van Beinum2007) implemented in ORCHESTRA, a framework for modelling the equilibrium and movement of chemicals (Meussen Reference Meussen2003).
The behaviour of the monovalent anion and cation was similar, as was that of the divalent ions. There was excellent agreement between model and observation for saturated flow, whether continuous or intermittent, but the model underestimated the outcomes of drained flow. Leaching from the micropores was slower for the divalent than for the monovalent ions, a consequence of the latter having diffusion coefficients approximately double those of the former: likewise, there was more movement of the monovalent ions from the macro to the microporosity during leaching. During intermittent leaching, with the flow in the macropores interrupted, ions redistributed from the centre to the periphery of the spheroids, leading to flushes of solute eluting when flow resumed. Consequently, intermittent leaching was more efficient than continuous leaching in removing solute from the microporosity, though the effect was less marked in drained than in saturated flow.
In ORCHESTRA, transport is calculated numerically by a mixing-cell algorithm: the number of calculation cells, their layout, and the boundary conditions are user-defined. The flexibility of ORCHESTRA enables modifications, e.g. a change in boundary conditions as in drained leaching, to be easily achieved as simulation proceeds. There is, however, no fitting needed, because the values of all parameters and variables are known or can be independently measured.
Citrus canker (CC) is a bacterial disease of citrus caused by the plant pathogen Xanthomonas axonopodis pv. citri (Gottwald Reference Gottwald2007). The disease is primarily spread by wind-blown rain and is present in many warm humid citrus-producing areas worldwide. CC has recently received significant media attention in Florida where a current epidemic of the disease threatens the $9 billion citrus industry. The epidemic was the subject of a 10-year eradication programme which involved the removal and destruction of millions of commercial and residential citrus trees (Graham & Gottwald Reference Graham and Gottwald2004). Given the substantial socio-economic costs associated with eradication it is essential that eradication programmes are designed to minimize the number of tree removals. This will depend upon the complex epidemiological interaction between the pathogen and the host landscape. A spatially explicit simulation model was constructed to describe the spread of CC in a mixed-host landscape (a ‘mixed-host landscape’ is a landscape which consists of both commercial citrus plantations and privately owned residential trees). An eradication programme was simulated whereby symptomatic trees, and trees within a predefined ‘control radius’ of a symptomatic tree, are removed to eliminate sources of inoculum. An optimal control radius is determined which achieves eradication and minimizes the number of trees removed. This radius differs depending on the topology of the host landscape and the relative importance assigned to residential and commercial trees. In general, eradication results in fewer trees being removed, and can be achieved in a shorter period, when the host landscape is fragmented. This result is particularly significant given that other citrus producing areas in the US (e.g. Arizona, California and Texas), which have yet to acquire the disease, are typically more fragmented than Florida suggesting that eradication may be less costly in the event of a future epidemic there.
This work was funded by the US Department of Agriculture.
Mean milk yield per lactation is currently approximately 7653 kg per cow in the UK (DEFRA 2007) and has increased at the rate of approximately 119 kg of milk per lactation per cow over the past 10 years. Concomitantly dairy herd fertility has decreased and therefore calving interval has increased by approximately 3 days per year and currently stands at approximately 410 days (1·123 years). Milk yield per cow per year has also increased but at a rate less than 119 kg per year, due to the extended calving interval. A deterministic model was produced based on explicit assumptions to predict the number of female replacement animals that will be available to: (1) replace the lactating cows currently being culled, which comprise approximately 0·30 of the national herd per annum; and (2) provide for national herd growth to supply increasing milk requirements due to human population growth in future. Under the current situation the UK national dairy herd could become unsustainable, due to an inability to produce sufficient female replacement animals in as little as 10 years (Maas et al. in press). The number of replacement female animals that will be available as replacement animals, calculated as a proportion of the herd size in future is dependent on five parameter values:
1. I 0, the current mean calving interval in years, current value 1·123 (years).
2. H, the proportion of calves born as females, currently approximately 0·50 (proportion).
3. S, the survival rate of female calves to first parturition at 2 years of age, currently approximately 0·70 (proportion).
4. ΔI, the annual increase in calving interval due to choices in nutrition, genetic selection and management that impact on fertility and thus calving interval. Currently calving interval is increasing at the rate of 3 days or 0·008219 (years) per year.
5. A f , the age of the replacement female at first calving (optimum approximately 2 years).
6. y, the number of years into the future for which model prediction is made (years).
Therefore the proportion of the national herd that will be available as replacement females in any future year y, is given by
The factor for future year is given as y−A f , to accommodate delay between animal birth and first parturition, heifers entering the lactating herd immediately post-partum were born A f years previously. Therefore using current UK parameter values, and a value of A f =2, in 20 years the proportion of the national herd available as replacements will be:

For illustration purposes, it is assumed that future mean lifespan, dairy cow import levels and the rate of increase production per cow per lactation remains constant at current values. If the current culling rate of 0·30 per annum is still occurring in 20 years, there will be a net deficit of 0·025 (0·300–0·275) of the national herd, or approximately 35 000 animals that would require importation to maintain the national herd at its current level, outwit any allowance for milk market growth to support increased future milk requirements. Obviously animal importation is associated with increased expense and risk of introduction of disease.
Figure 1 shows model predictions for proportion of the herd available as replacement animals for 20 years in future, altering the value of ΔI from a value of −0·008219 to 0·016438 years, equivalent to a range of annual calving interval changes of −3 days to +6 days respectively. These results suggest that in future, the dairy industry must balance selection and management goals for both increased fertility and production and all available techniques must be employed to increase fertility, thereby halting or even reversing the currently increasing calving interval of the national herd if it is to be self-sustaining in future.
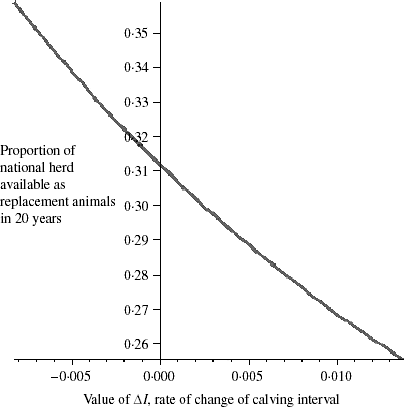
Fig. 1. Number of females available as replacement animals, as a proportion of total herd size, in 20 years as a function of ΔI. Values of ΔI correspond to annual changes in calving interval ranging between −3 and +6 days (−0·008219 and +0·016438 years respectively).
When a strongly sorbed solute such as H2PO4− is incubated with a portion of soil, the reaction is often rapid at first but then continues at a slower rate for some time, so that the final equilibrium distribution between solid and solution is many times that after the initial period (Nye & Staunton Reference Nye and Staunton1994). Further, the rate is sensitive to experimental conditions. A long-standing question is the extent to which the rate processes behind such phenomena are controlled by access to sorption sites in the soil, for example via narrow pores connecting dead-end regions to the main soil pore network, as distinct from slow surface reactions per se. The answer has implications for how we model the fate and behaviour of strongly sorbed solutes in soil and uptake by plant roots.
To explore this issue the diffusive transport of a strongly sorbed solute in soil and its adsorption on surfaces inside and outside soil particles has been modelled. It is considered that the soil consists of a series of uniformly spaced porous spherical particles surrounded by soil solution and air. This corresponds to the experimental situation where soil has been sieved to give roughly uniform micro-aggregates. The inter- and intra-particle spaces are considered separately. A diffusion equation defined in the inter-particle space coupled with ordinary differential equations for solute binding on the particle surfaces is introduced. The flux of solute from the inter- to intra-particle space is prescribed and the concentration at the particle surface is taken to be continuous. The change in concentration inside the particle is defined by the reaction–diffusion equation and ordinary differential equations describing the binding to the surfaces inside the particle. The surface binding reactions inside and outside the particle are considered to be the same, and, crucially, it is assumed that these reactions take place in two stages that can be modelled by separate slow and fast reactions.
Using homogenization theory (Hornung Reference Hornung1997), a macroscopic model is derived for the distribution of the average solute concentration defined in the simple homogeneous domain. This homogenization procedure simplifies the numerical computation. Numerical solutions of the macroscopic model are illustrated in Fig. 1.

Fig. 1. L e, L i, amounts of solute in solution in inter- and intra-particle space; S e, S i, amounts on particle surfaces in inter- and intra-particle space; P, total amount of solute in the soil; x, longitudinal direction of the soil; r, macroscopic particle radius; t, time, t=10 days.
Specific weight (weight per unit volume) of harvested wheat grain is a criterion of quality used in trading. It is linearly related to the preceding winter index of the North Atlantic Oscillation (NAO), a large-scale atmospheric pressure difference between Iceland and the Azores (Kettlewell et al. Reference Kettlewell, Sothern and Koukkari1999). The mechanism underlying the association appears to be through a lag relationship of the winter NAO index with the following summer sunshine duration and rainfall, both of which affect grain specific weight (Kettlewell et al. Reference Kettlewell, Sothern and Koukkari2003; Atkinson et al. Reference Atkinson, Kettlewell, Hollins, Stephenson and Hardwick2005). A linear regression model of national mean specific weight, weighted with sample number, on winter NAO index has been developed to forecast wheat quality well in advance of harvest.
The optimal NAO index for forecasting, calculated from gridded pressure data, involves too much computation for regular annual forecasts and, although less correlated with specific weight, the pre-calculated Climate Prediction Centre (CPC) index is now used. There is little evidence of serial correlation in either the specific weight or the CPC NAO time series over the period for which national specific weight data is available (1974 onwards), indicating the validity of a simple regression model. Cross-validation over the years 1974–2007 indicates that the model is likely to correctly forecast whether specific weight is above or below the long-term mean with an accuracy of 71% compared with 50% by chance (χ2=5·40, 1 d.f., P=0·02).
Studies with historical data from the Broadbalk Wheat Experiment have shown that the model is temporally unstable. Running correlations of the NAO with the contemporary national data used for forecasting indicate that the association may have weakened slightly in recent years. Investigating spatial stability has proved more difficult due to lack of georeferenced specific weight data. Gridded correlations of the winter NAO with summer rainfall, representing one of the underlying mechanisms, indicate that the model is most applicable in Eastern England. Fortuitously, this is where most of the UK wheat is grown. Annual forecasts are posted in spring at: http://www.harper-adams.ac.uk/groups/crops/wheat/
UK dairy systems rely heavily on grass-based diets to support milk production, particularly throughout the summer months. On such diets the supply of glucogenic nutrients may be limiting to production. Existing feed evaluation systems are used widely to estimate the requirement for energy under grazing conditions to support a given level of milk yield. However, these systems assess the animal's requirements according to metabolizable energy (ME) or net energy (NE) and do not consider the characteristics of the energy delivering nutrients. Unlike their empirical alternatives, mechanistic models take into account the site of digestion, the type of nutrient absorbed and the type of nutrient required for production of milk constituents. The objective of this study was to compare energy or nutrient supply on grass-based diets with the energy or nutrients required for observed milk production calculated from empirical energy systems and from a mechanistic model. The energy systems investigated were the AFRC ME system, the Feed Into Milk (FIM) system and the Dutch NE system. The mechanistic model was based on Dijkstra et al. (Reference Dijkstra, France, Assis, Neal, Campos and Aroeira1996) and Mills et al. (Reference Mills, Dijkstra, Bannink, Cammell, Kebreab and France2001). The dataset for evaluation consisted of 41 records from 11 experiments of grass-based diets (at least 75% grass on dry matter basis) that had sufficient information to calculate supply and requirement according to each model. Assessment of the error of energy or nutrient supply relative to requirement was made by calculation of the mean square prediction error (MSPE). In the mechanistic model, the supply of glucogenic nutrients was always more limiting to milk production than the supply of aminogenic nutrients or the supply of energy. The residual MSPE (expressed as a percentage of the supply) was lowest for the mechanistic model (6·1%), followed by the Dutch NE system (8·2%), FIM ME system (9·7%) and AFRC ME system (11·8%). In all models, the observed energy or nutrient supply exceeded the calculated energy or nutrient requirement. For the energy evaluation systems, the error due to overall bias of prediction dominated (>50%) the MSPE, whereas for the mechanistic model, 76% of MSPE was due to random variation. The FIM ME system gave a slightly improved prediction of requirements than the AFRC ME system. Analysis of the difference between supply and requirement indicated a relationship with the protein content of the grass for the Dutch NE system, but this relationship was absent for the other models. The grass dry matter intake level was positively related to the difference between supply and requirement for all models, in particular the mechanistic model and the ME systems. In conclusion, current requirements-based energy evaluation systems overestimate energy supply relative to energy requirement on grass-based diets for dairy cattle. The mechanistic model predicted glucogenic nutrients to limit milk production. The model overestimated dietary nutrient supply especially at higher intakes but overall it proved to be more reliable than the empirical energy systems.
Ruminant livestock have been highlighted as a source of greenhouse gas emissions resulting from the production of methane during anaerobic fermentation in their digestive tract (Johnson & Johnson Reference Johnson and Johnson1995). Several studies have described attempts to reduce methane emissions through nutritional or pharmacological means with varying degrees of success. However, these studies have tended to ignore the contribution of exhaled carbon dioxide (CO2) to the animal's carbon footprint. The aims of this research were to determine the relative importance of exhaled CO2 and methane to the carbon footprint of lactating dairy cows and to examine their relationship to dietary intake. A locally derived database comprising 186 individual measurements of respiratory exchange and methane emission from lactating dairy cows was analysed. The mean dry matter intake (DMI) was 18·4 kg/d (range 10–28 kg/d) from a broad range of diet types based on grass silage, maize silage or fresh grass. As shown in earlier studies, methane was closely related to DMI. Carbon dioxide output also showed a strong linear correlation with DMI. In order to estimate the carbon footprint of each animal, 1 kg methane was assumed to yield a CO2 equivalent of 25 kg (Forster et al. Reference Forster, Ramaswamy, Artaxo, Berntsen, Betts, Fahey, Haywood, Lean, Lowe, Myhre, Nganga, Prinn, Raga, Schulz, Van Dorland, Solomon, Qin, Manning, Chen, Marquis, Averyt, Tignor and Miller2007). The carbon footprint of each animal was assumed to be a function of exhaled carbon dioxide and methane emissions combined. Emissions from manure were not included in this analysis. Methane accounted for a mean of 0·44 of each animal's carbon footprint with a range of 0·34–0·50. This variation in methane emissions as a proportion of total CO2 equivalent output was not associated with the level of DMI. National greenhouse gas inventory data tend to limit their focus to methane output. If an estimate of CO2 output were added to the inventory for the UK's 2 million lactating dairy cattle this would be an annual CO2 emission of approximately 6·5 million tonnes. This would be in addition to the 0·2 million tonnes of methane from these cattle annually (equivalent to 4·2 million tonnes of CO2 equivalents). This study shows the importance of a broader scope to include CO2 from respiratory exchange, its contribution being greater than that of methane from the digestive tract. Mitigation strategies aimed at reducing methane emissions should be set in this context.
The financial support of UK DEFRA project LS3656 is gratefully acknowledged.



