Discussions of troop requirements and weaponry for NATO have been much concerned with the battlefield consequences of different troop strengths and nuclear doctrines. But the battlefield criterion is only one criterion, and when nuclear weapons are introduced it is secondary. The idea that European armament should be designed for resisting Soviet invasion, and is to be judged solely by its ability to contain an attack, is based on the notion that limited war is a tactical operation. It is not. What that notion overlooks is that a main consequence of limited war, and potentially a main purpose for engaging in it, is to raise the risk of larger war.
—Thomas C. Schelling, Arms and Influence, 1966The defining feature of international politics since 1945 has been the absence of direct great power conflict.Footnote 1 To explain this historical anomaly, some scholars classify this “long peace” as the “nuclear peace,” where the fear of a nuclear exchange prevents significant conflict among great powers.Footnote 2
How the nuclear peace functions in practice is subtle. It is not as if states can credibly deter all revisionist behavior through the threat of a nuclear first strike. After all, unless it is facing an existential threat, no state would ever intentionally launch a strategic nuclear strike against an opponent with a credible second-strike capability, as doing so would be tantamount to suicide. And the existence of nuclear weapons does not prevent states from fighting conventional wars over non-existential issues. In theory, states with nuclear weapons could forgo them and fight conventional conflicts with one another, just as they did before the advent of nuclear weapons. Instead, what preserves the nuclear peace is the threat of unintended escalation.Footnote 3 In the nuclear era, any conventional conflict is unstable and could accidentally or inadvertently escalate to a nuclear exchange. Proponents of the nuclear peace suggest that the near absence of large-scale, direct conventional conflict between nuclear states stems from this new and unsettling reality.Footnote 4
While the nuclear peace can be rationalized within the current theoretical framework connecting conventional conflict to nuclear escalation, other salient features of the nuclear era are more difficult to understand. Scholars have theorized that the nuclear era should be a period of limited wars and restraint, where deterrence becomes easier.Footnote 5 Yet the nuclear peace has come at exceptionally high cost. During the Cold War, both the Warsaw Pact and NATO spent enormous sums on conventional capabilities every year (in absolute terms) preparing for a conventional assault by their opponents.Footnote 6 Despite predictions that the nuclear era would be a period of restraint, no state in the Cold War expected its opponents to actually use such restraint, and they armed themselves accordingly. And while there have undoubtedly been instances of nuclear-armed states exhibiting restraint in crises (in the Kargil War, for example), the Soviet Union also showed little restraint in repressing revolutionary movements within its sphere of influence in Eastern Europe, despite the possibility of Western intervention. What then explains the nuclear era, where peace largely persists between nuclear powers, there is an extensive conventional force buildup, and international crises can feature either restraint or aggressive military maneuvers?
To better understand state behavior in the nuclear era, we must follow Schelling’s insight: conventional force posture shapes both the conventional balance of power and the risk of a nuclear war. Here I model a deterrence setting between two states in a crisis over an asset. The asset in dispute is important to both, but not important enough for either to deliberately launch a strategic nuclear first strike to deny its opponent the asset (it is not a matter of existential importance). Instead, states may be willing to engage in a conventional conflict over the asset; but unlike in traditional deterrence models, this scenario introduces a particular risk: that the conflict could accidentally or inadvertently escalate into a strategic nuclear exchange, capturing the essence of brinkmanship.Footnote 7
Using this model, I establish two key theoretical results. First, accounting for the risk of inadvertent nuclear escalation may require states to increase or decrease their spending on conventional forces for deterrence, compared to what they would spend in a world without nuclear weapons. Why? If a conventional conflict could escalate into a nuclear exchange, all actors fare worse in a conventional-but-now-potentially-nuclear conflict. In cases where imposing costs on a challenger is essential for deterrence, increasing nuclear risk makes a conventional war worse for the challenger, thereby allowing a defender to deter a challenger with lower levels of conventional arming. For the purpose of imposing costs on a challenger, nuclear risks reinforce conventional force postures. However, in cases where deterrence hinges on a defender’s willingness to escalate in response to a challenge, increasing nuclear risk makes a conventional war worse for the defender, thereby requiring a defender to arm more to be willing to escalate. For the purpose of keeping a defender motivated to fight, nuclear risks can undermine the deterrent threat from a conventional force posture. In contrast to other writing on the matter,Footnote 8 this latter result suggests that credibility remains an issue in extended deterrence in the nuclear era.
Second, actors in the nuclear era will sometimes demonstrate restraint, while at other times they will act more aggressively and decisively than they otherwise would. This duality can be explained through the logic of how nuclear risk is generated within a conventional conflict. Conventional conflicts could become strategic nuclear exchanges through accidents, decentralized decision making, or inadvertent escalation.Footnote 9 Across all these mechanisms, the time spent in conflict is critical. When conflicts between nuclear powers are short and decisive, there are fewer opportunities for unintended escalation leading to a nuclear exchange; if a conventional conflict in the nuclear era is a war of nerves similar to “rocking the boat,”Footnote 10 then the shorter the time spent rocking, the less likely actors are to get soaked. Nuclear risk incentivizes actors to take steps that will make a conflict more decisive, which can lead to more or less aggressive force postures (whichever leads to shorter conflicts).
To the best of my knowledge, these two theoretical results are new. However, findings like these are valuable only insofar as they explain real-world behavior that the existing state-of-the-art theories cannot rationalize. The finding that nuclear risk may incentivize actors to act more decisively in a conflict offers insight into the Soviet repression of the 1956 Hungarian Revolution and recent (2019) Indian activity in Kashmir. In both cases, rather than act with restraint as past research would predict,Footnote 11 actors took decisive actions to quickly resolve the conflicts. The theory presented here suggests that these actors may have behaved more aggressively to avoid the nuclear risks of a protracted conflict. And the finding that nuclear risk does not always complement conventional forces offers insight into the challenges the Eisenhower administration faced in attempting to replace an expansive conventional force posture with strategic nuclear weapons, and why the West relied on nuclear risks for the defense of West Germany while avoiding nuclear risks in the Vietnam War.
This paper also identifies a series of other results. It offers a new formal theoretical grounding for the nuclear peace. It offers some additional support for (and qualifiers to) the stability–instability paradox. It describes how increasing nuclear instability can (perversely) lead to more instances of deterrence failure. It discusses how aspects of the nuclear revolution beyond strategic nuclear weapons—like tactical nuclear weapons—shape our understanding of deterrence. And it establishes how, in an incomplete-information environment, using conventional force posture to signal resolve can lead to fewer instances of conflict and a lower risk of a nuclear exchange relative to signaling with nuclear risk (as examined by Powell).Footnote 12
This paper is related to others that consider crises where multiple levels of conflict are feasible.Footnote 13 The key difference here is that, because I consider accidental or inadvertent nuclear escalation, escalation from the lower (conventional) to higher (nuclear) level is probabilistic. This approach is most similar to that of Powell,Footnote 14 who also considers nuclear risk stemming from a conventional conflict. However, Powell applies a different theoretical grounding to how nuclear risk is generated, and his results generally suggest that actors will behave with restraint; this means that Powell can explain cases like the Kargil War but not the Hungarian Revolution or India’s recent activity in Kashmir (as discussed further later). This paper is also naturally related to the topic of nuclear proliferation,Footnote 15 but here it is already established that both sides possess a nuclear capability.
On Conventional Force Posture, Conventional Conflict, and Nuclear Risk
I assume that there is a non-monotonic (increasing-then-decreasing) relationship between the defender’s conventional force posture and nuclear escalation risk. To summarize, this structure rests on three key relationships, which together imply that increasing one’s conventional force posture could make conflict more or less decisive, which could lead to less or more nuclear risk (respectively).
Adding conventional forces can increase or decrease military parity. This first relationship is mechanical. Adding conventional forces can narrow the gap between two sides if the defender’s capabilities approach the challenger’s, or widen it if the defender’s capabilities surpass the challenger’s.
Closer military parity between actors results in longer conflicts. If military parity is low, then a decisive war or a rapid surrender is more plausible. But if militaries are more evenly matched, then neither side has an immediate reason to stop fighting. Because closely matched militaries will trade battle victories and defeats, war between them will be less informative or less clearly decisive, which will incentivize them to continue fighting. This logic is illustrated in a series of theoretical models,Footnote 16 echoed by empirical findings.Footnote 17
Longer conflicts generate a greater likelihood of a nuclear exchange. Conventional conflicts could escalate to a nuclear exchange through several mechanisms. First, it could arrive entirely through accident. In any complex system, including missile detection or early warning systems, system failures are possible.Footnote 18 When states are at war, there is heightened risk of a faulty signal being interpreted as an act requiring a nuclear response.Footnote 19 Nuclear escalation could also arise through the course of conventional conflict operations. Whether through mechanical error (a malfunctioning GPS), human error (misread maps), agency problems, or the fog of war, sometimes soldiers or operators take actions beyond what a rational, unitary decision maker would want, which could make a crisis over an auxiliary issue seem existential and necessitate escalation.Footnote 20 Also, in a protracted conventional war, states may target their opponent’s communication or command-and-control infrastructure, which could inadvertently undermine the targeted state’s second-strike capability, risking nuclear escalation.Footnote 21 While these risks are typically ascribed to newer nuclear states, all states implement some degree of decentralized decision making or risk detection within crises or conflicts that can result in some risk of accidental escalation.Footnote 22 Recent research suggests this dynamic may be further exacerbated by how states respond to cyber capabilities and vulnerabilities.Footnote 23
In all these different ways that a conventional conflict could turn nuclear, time is a critical factor. When conventional conflicts between nuclear powers are short and decisive, there are fewer chances or reasons for system failures, overambitious operations, or the targeting of command-and-control infrastructure. But as conflicts become protracted, the likelihood of errors leading to a strategic nuclear exchange increases. Taking these considerations together, if a defender’s force posture ensures a swift, one-sided conflict, then the risk of nuclear escalation is low.Footnote 24 But if the defender’s force posture lends itself to a prolonged conventional conflict, then the risk of a nuclear exchange will be greater.
Model
Game Form and Assumptions
Two players, a challenger (C) and a defender (D), are in a deterrence game with complete information. The game order is as follows (Figure 1).
-
1. D selects a conventional force posture (or arming level)
$p \in \left[ {{p_0},{p_1}} \right]$
, which is D’s likelihood of winning in a conventional conflict. I assume
$0 \lt {p_0} \lt {p_1} \lt 1$
.Footnote
25
-
2. C selects whether to challenge or not.Footnote 26 If C does not challenge, the game ends with C receiving payoff
$0$
and D receiving payoff
${v_{\rm{D}}} - K\left( p \right)$
, where
$K:{\mathbb{R}_ + } \to {\mathbb{R}_ + }$
is D’s costs from the conventional force level. I assume
$K\left( {{p_0}} \right) = 0$
, and
$K$
is continuous and increasing in
$p$
. If C does challenge, the game moves to the next stage. -
3. D selects whether to acquiesce or to escalate to conflict. If D acquiesces, C receives payoff
${v_{\rm{C}}}$
and D receives payoff
$ - K\left( p \right)$
. If D escalates to conflict, then both states receive their conflict payoffs (described later).
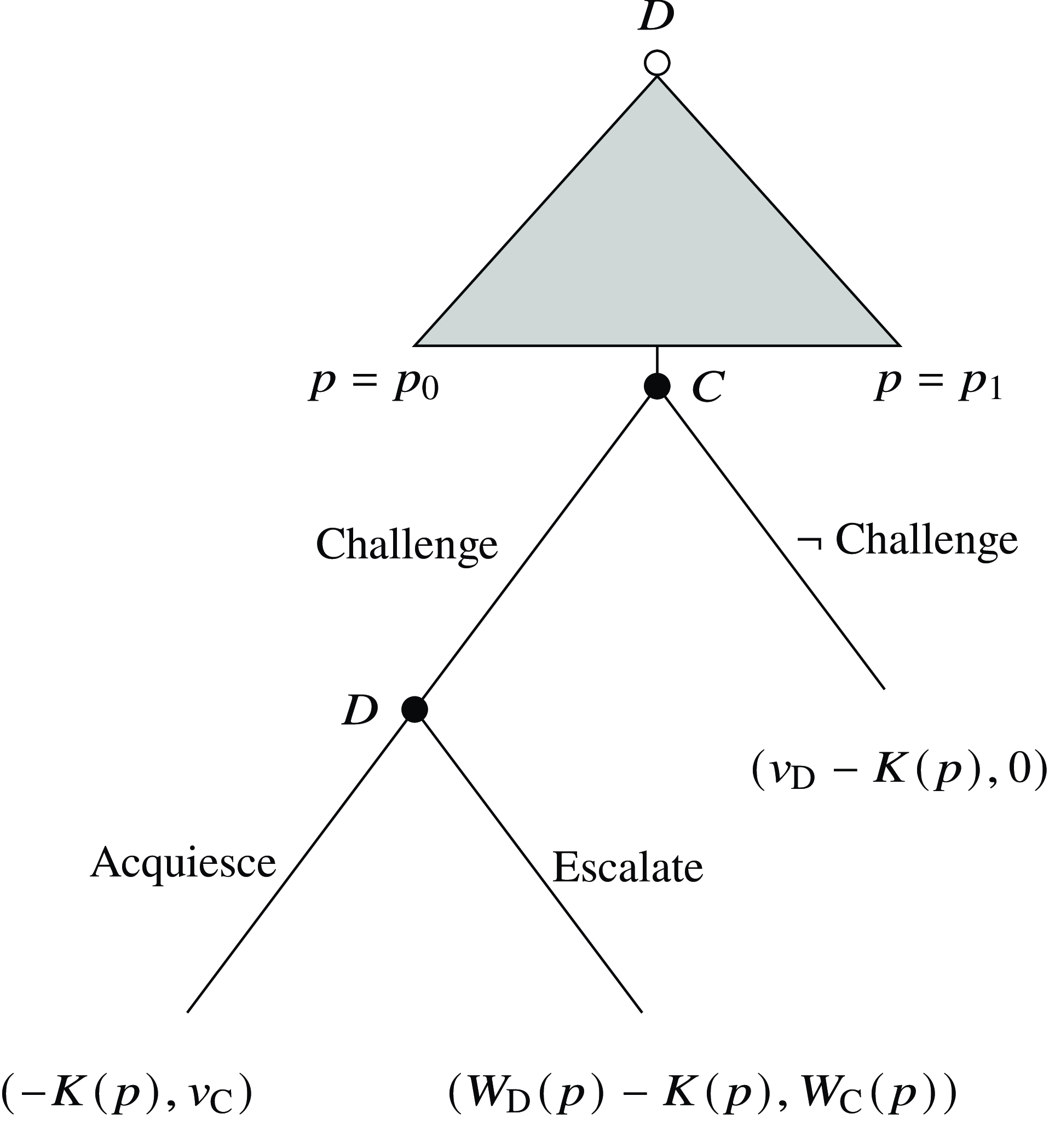
FIGURE 1. The game tree, with payoffs in parentheses
Conflict is a reduced-form, stochastic process that will end in one of three outcomes: C wins a conventional victory, D wins a conventional victory, or there is a catastrophic nuclear exchange. Because actors do not “move” within the conflict, conflict duration and outcome will be shaped by endogenous selections (in
$p$
) and several exogenous hazard rates, which characterize the likelihood of a given conflict outcome occurring at any point in time.Footnote
27
I let
$t$
denote time, and if D chooses to escalate, then conflict starts with
$t = 0$
.
Let
$n \ge 0$
denote the hazard rate for the termination of the conflict through a nuclear exchange. Essentially, this is the “nuclear instability” of a conflict; it takes on greater values when C or D are more accident prone, have more decentralized or automated nuclear launch decisions, have a larger nuclear arsenal, are fighting near critical nuclear infrastructure, or, for conflict below the level of a strategic nuclear exchange, are using tactical nuclear weapons.Footnote
28
The case when
$n = 0$
is particularly significant. It reflects a scenario with no risk of nuclear escalation, which was a feature of great power conflict before the nuclear revolution. Following the logic discussed earlier, I let
${\alpha \over {p\left( {1 - p} \right)}}$
denote the hazard rate for the termination of conflict through conventional means. I have defined the choice variable
$p$
; for lopsided conflicts (
$p \approx 0$
or
$p \approx 1$
) the hazard rate is large, which is consistent with one-sided conventional conflicts ending quickly.Footnote
29
The parameter
$\alpha \gt 0$
scales the hazard rate for conflict ending conventionally relative to the hazard rate for conflict ending with a nuclear exchange. It follows that
$h\left( p \right) = n + {\alpha \over {p\left( {1 - p} \right)}}$
is the hazard rate for conflict ending in the next unit of time;
$n/h\left( p \right)$
is the likelihood that conflict ends in a nuclear exchange;
${\alpha \over {h\left( p \right)p\left( {1 - p} \right)}}$
is the likelihood that conflict ends conventionally; and
${1 \over {h\left( p \right)}}$
is the expected time to conflict termination.
If the game ends with a nuclear exchange, D’s and C’s expected payoffs are
$ - {N_{\rm{D}}} \lt 0$
and
$ - {N_{\rm{C}}} \lt 0$
, respectively. If the conflict ends conventionally, D wins with probability
$p$
, and C wins with probability
$1 - p$
. As in Powell’s treatment,Footnote
30
there is no repeated play, so
$p$
can most cleanly be thought of as mobilization levels within a crisis, but could also be interpreted as long-term investments in deterrence of an area.Footnote
31
However the conflict ends, by fighting, actors accrue conventional conflict costs at the rate
${c_{\rm{D}}} \ge 0$
and
${c_{\rm{C}}} \ge 0$
, respectively.
C’s expected utility from conflict is
$${W_{\rm{C}}}\left( p \right) = {n \over {h\left( p \right)}}\left( { - {N_{\rm{C}}}} \right) + {\alpha \over {h\left( p \right)p\left( {1 - p} \right)}}\left( {\left( {1 - p} \right){v_{\rm{C}}}} \right) - {{{c_{\rm{C}}}} \over {h\left( p \right)}},$$
and D’s expected utility—without considering arming costs
$K\left( p \right)$
—is
$${W_{\rm{D}}}\left( p \right) = {n \over {h\left( p \right)}}\left( { - {N_{\rm{D}}}} \right) + {\alpha \over {h\left( p \right)p\left( {1 - p} \right)}}\left( {p{v_{\rm{D}}}} \right) - {{{c_{\rm{D}}}} \over {h\left( p \right)}}.$$
Figure 2 illustrates the likelihood of a nuclear exchange and D’s expected utility (without arming costs,
$K\left( p \right)$
), from a conflict for a range of possible
$p$
’s under one set of parameters. First, consider the likelihood of nuclear exchange (solid line). For small or large conventional arming levels (
$p \approx 0$
and
$p \approx 1$
),
$h\left( p \right)$
becomes large and
$h\left( p \right)p\left( {1 - p} \right)$
becomes small; thus, when the conventional arming level leads to an unbalanced or one-sided conventional conflict, there is little risk of a nuclear exchange (
${n \over {h\left( p \right)}}$
is smaller) and there is a greater likelihood of the conflict ending conventionally (
${\alpha \over {h\left( p \right)p\left( {1 - p} \right)}}$
is greater). In a more balanced conventional conflict (
$p \approx {1 \over 2}$
), there is greater risk of nuclear exchange and a (relatively) lower likelihood the game ends with a conventional victory or defeat.
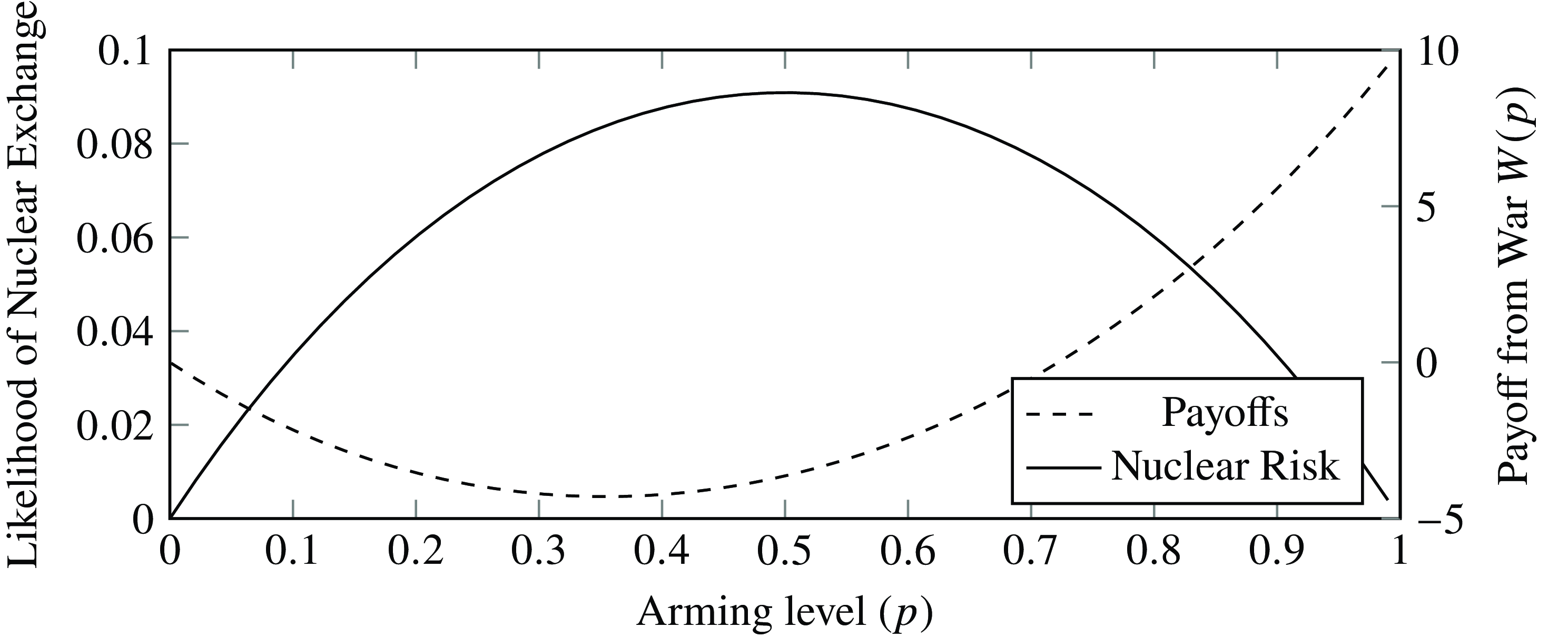
FIGURE 2. Nuclear risk and payoffs with the costs of arming excluded
Note: Parameters for this figure (and all other figures) are in the online supplement.
Now consider D’s payoff from conflict without arming costs (dashed line). As
$p$
increases from
$0$
to roughly
$0.35$
, the conflict becomes more protracted, and the increasing risks of a nuclear exchange reduce D’s payoff. Then, for
$p$
values greater than
$0.35$
, the defender continues becoming more likely to win the conflict, and the nuclear risk increases more slowly and then eventually decreases; thus D’s utility switches to increasing in
$p$
until reaching
${p_1}$
. Note that the non-monotonicity in utility follows from this parameter set; while D’s fighting utility will always be increasing for
$p \ge 0.5$
, the payoff from fighting could be increasing over the full range under alternate parameters.Footnote
32
Comments on Model Assumptions
This is a deterrence model.Footnote 33 The model setup is most similar to Powell’s,Footnote 34 but differs in two key respects. First, in the model presented here, nuclear risk in a conventional conflict is determined indirectly through the defender’s arming level. In Powell, the defender is able to directly manipulate the level of nuclear risk within a conventional war without altering its likelihood of winning in the conventional war. Second, Powell finds that adding conventional forces to a conflict always increases the risk of escalation. Unlike this model, Powell does not consider that a swift and decisive deployment might reduce the likelihood of a nuclear exchange by preventing a prolonged conflict. Naturally, these different assumptions lead to different results, as highlighted throughout the paper; for details, see the online supplement.
I have benefited from decades of iterations of models of nuclear deterrence.Footnote 35 I will not cite the entire set of studies on nuclear deterrence but refer readers to several excellent reviews.Footnote 36 The model also integrates features from the formal literature on endogenous transgressions and deterrence.Footnote 37 Of course, nearly every model just cited considers only two types of outcomes: war and peace. This paper is related to a new branch of research that considers conflict that can be more multifaceted.Footnote 38
Important scope conditions apply to the results. The model is well suited to describe crises between two nuclear-armed states that are not over existentially important issues: in this model, actors cannot launch a strategic nuclear missile when faced with the prospect of an opponent seizing the asset. Instead, the model can capture settings where actors are willing to escalate to conventional conflict with nuclear risks. It encompasses scenarios with low nuclear risk, such as Cold War crises in Eastern Europe,Footnote
39
as well as higher-risk conflicts, like those involving newer nuclear states, such as Pakistan, India, or North Korea, where missteps in nuclear command and control may be more likely. As a special case, the model can also describe crises where conventional conflict generates no nuclear risk (formally,
$n = 0$
), as in the era before nuclear weapons were developed. That said, it cannot describe every crisis during the Cold War—for example, it does not cover the Second Taiwan Strait Crisis (where China did not possess a nuclear weapon) or the Cuban Missile Crisis (where nuclear escalation risk was generated outside of conflict).
Equilibrium
D’s initial arming selection will shape how D and C behave, ultimately leading to three different equilibrium paths. First, D could not arm, resulting in C challenging, D acquiescing, and C getting the asset. Second, D could arm to deter C, resulting in D holding on to the asset. And third, D could arm to a level where C and D will fight.
To deter C, D must select a conventional force level where two conditions hold: (a) D is willing to fight when challenged, and (b) C knows that fighting D is sufficiently bad for it. When condition (a) is met, D has selected force posture that satisfies its war participation constraint, meaning at or beyond the minimum level where D would be willing to fight if challenged. Formally, this is any
$p \ge {p^{\rm{D}}}$
, whereFootnote
40
$${p^{\rm{D}}} = 1 - {{{\alpha _{\rm{D}}}} \over {{c_{\rm{D}}} + n{N_{\rm{D}}}}}.$$
To remain willing to fight when challenged, D must select greater conventional force postures
${p^{\rm{D}}}$
if
${c_{\rm{D}}}$
,
${N_{\rm{D}}}$
, and
$n$
increase, and if
$\alpha $
and
${v_{\rm{D}}}$
decrease. Why? As some intuition, increasing
${c_{\rm{D}}}$
,
${N_{\rm{D}}}$
, and
$n$
all increase the costs from war, decreasing
$\alpha $
makes the nuclear outcome option more likely, and decreasing
${v_{\rm{D}}}$
makes D value the asset less; faced with these changes, D would be willing to fight only if D wins the asset with higher likelihood, necessitating an increased
$p$
.
For deterrence condition (b) to be met, D must select a force posture that meets C’s war cost constraint—where C’s costs from going to war outweigh C’s benefits from challenging. Formally, this is any
$p \ge {p^{\rm{C}}}$
,Footnote
41
which satisfies
$${p^{\rm{C}}} = \;\;{{\alpha {v_{\rm{C}}}} \over {{c_{\rm{C}}} + n{N_{\rm{C}}}}}.$$
The value
${p^{\rm{C}}}$
is decreasing in
${c_{\rm{C}}}$
,
$n$
, and
${N_{\rm{C}}}$
, and increasing in
$\alpha $
and
${v_{\rm{C}}}$
. As intuition, as C’s costs from going to war increase (
$n$
,
${N_{\rm{C}}}$
, and
${c_{\rm{C}}}$
all increase and
$\alpha $
decreases) or C’s valuation of the asset (
${v_{\rm{C}}}$
) decreases, C is less willing to go to war, which makes it easier to deter C at lower force postures.
Thus, for deterrence, D will select the smallest force posture where D’s war participation constraint and C’s war cost constraint are both met—formally, if D sets
$p = {\rm{max}}\left\{ {{p^{\rm{C}}},{p^{\rm{D}}}} \right\}$
, C will be deterred. Importantly, only one constraint will bind. When C’s war cost constraint binds (
${p^{\rm{D}}} \lt {p^{\rm{C}}}$
), D can arm to a level where D is willing to fight, but must arm further to make war sufficiently costly for C to deter C. When D’s war participation constraint binds (
${p^{\rm{D}}} \gt {p^{\rm{C}}}$
), so long as D has armed to a level where D is willing to fight, C will be deterred.
Alternatively, sometimes D and C will fight. Suppose D has armed to a level where D’s war participation constraint is met but C’s war cost constraint is not met—this results in war. Formally, whenever
${p^{\rm{D}}} \lt {p^{\rm{C}}}$
, D may prefer selecting some arming level that results in fighting.Footnote
42
When fighting, D optimizes by setting
$p = \hat p$
, where
$$\hat p \in \mathop {{\rm{argmax}}}\limits_{p \in \left[ {{\rm{max}}\left\{ {{p^{\rm{D}}},{p_0}} \right\},{\rm{min}}\left\{ {{p^{\rm{C}}},{p_1}} \right\}} \right]} \left\{ {{W_{\rm{D}}}\left( p \right) - K\left( p \right)} \right\}$$
I define D’s utility from setting
$p = \hat p$
as
${U_{\rm{D}}}\left( {\hat p} \right)$
.Footnote
43
Finally, D may opt not to arm. If D does not value the asset much or faces high costs to arming, D may select the smallest force posture and acquiesce when challenged.
In addition to assuming that equilibria must be subgame perfect, I also assume:
Complete-information game assumption: There is a feasible level of arming where D is willing to fight. Formally,
${\rm {p}^{\rm{D}}} \le {\rm {p}_1}$
.
This assumption rules out a fairly uninteresting case. If
${p^{\rm{D}}} \gt {p_1}$
, then D’s war participation constraint is never met, making deterrence impossible and outside of the scope of interest.
With this assumption in place, I can describe the equilibrium behavior. To summarize the intuition around the three cases in the Proposition, D’s arming decision depends on what arming options are available and what gives D the greatest utility. For example, suppose C’s war cost constraint cannot be met (
${p^{\rm{C}}} \gt {p_1}$
), which means D cannot ever keep C from challenging and therefore cannot deter C. Whenever
${p^{\rm{C}}} \gt {p_1}$
, D will choose between (a) not arming and acquiescing (setting
$p = {p_0}$
) and (b) going to war (setting
$p = \hat p$
), depending on which gives D the greater utility. Alternatively, suppose D’s war participation constraint binds, meaning D being willing to fight is enough to deter C (
${p^{\rm{C}}} \le {p^{\rm{D}}}$
). Here, D chooses between deterring C and acquiescing. The equilibrium is as follows.
Proposition 1: There exists an essentially unique subgame perfect equilibrium taking the following form.Footnote
44
Working backwards, if challenged, D will fight whenever
$p \ge {p^{\rm{D}}}$
and will acquiesce otherwise. Before D fights or acquiesces, C will challenge, unless both
$p \ge {p^{\rm{C}}}$
and
$p \ge {p^{\rm{D}}}$
. And, before C challenges or not, D will select the following arming levels (letting
${p^{\rm{*}}}$
denote equilibrium arming levels).
-
Case 1. When
${p^{\rm{D}}} \lt {p^{\rm{C}}} \le {p_1}$
,-
– If
${p^{\rm{D}}} \ge {p_0}$
,
${V_{\rm{D}}} - K\left( {{p^{\rm{C}}}} \right) \ge 0$
and
${V_{\rm{D}}} - K\left( {{p^{\rm{C}}}} \right) \ge {W_{\rm{D}}}\left( {\hat p} \right) - K\left( {\hat p} \right)$
, or
${p^{\rm{D}}} \lt {p_0}$
and
${V_{\rm{D}}} - K\left( {{p^{\rm{C}}}} \right) \ge {W_{\rm{D}}}\left( {\hat p} \right) - K\left( {\hat p} \right)$
, then D selects
${p^{\rm{*}}} = {p^{\rm{C}}}$
(D deters C). -
– If
${p^{\rm{D}}} \ge {p_0}$
,
$0 \gt {V_{\rm{D}}} - K\left( {{p^{\rm{C}}}} \right)$
, and
$0 \gt {W_{\rm{D}}}\left( {\hat p} \right) - K\left( {\hat p} \right)$
, then D selects
${p^{\rm{*}}} = {p_0}$
(D acquiesces). -
– Otherwise, D selects
${p^{\rm{*}}} = \hat p$
(D and C fight).
-
-
Case 2 (deterrence is impossible). When
${p^{\rm{D}}} \lt {p^{\rm{C}}}$
and
${p^{\rm{C}}} \gt {p_1}$
,-
– If
${p^{\rm{D}}} \ge {p_0}$
and
${W_{\rm{D}}}\left( {\hat p} \right) - K\left( {\hat p} \right) \ge 0$
, or
${p^{\rm{D}}} \lt {p_0}$
then D selects
${p^{\rm{*}}} = \hat p$
(D and C fight). -
– Otherwise, D selects
${p^{\rm{*}}} = {p_0}$
(D acquiesces).
-
-
Case 3 (fighting is impossible). When
${p^{\rm{C}}} \le {p^{\rm{D}}}$
,-
– If
${p^{\rm{D}}} \ge {p_0}$
and
${V_{\rm{D}}} - K\left( {{p^{\rm{D}}}} \right) \ge 0$
, or
${p^{\rm{D}}} \lt {p_0}$
, then D selects
${p^{\rm{*}}} = {\rm{max}}\left\{ {{p_0},{p^{\rm{D}}}} \right\}$
(D deters C). -
– Otherwise, D selects
${p^{\rm{*}}} = {p_0}$
(D acquiesces).
-
Proofs are given in the online supplement.
Figure 3 displays the logic of Proposition 1 for one set of parameters.
${v_{\rm{D}}}$
values are increasing on the x-axis, and
${v_{\rm{C}}}$
values are increasing on the y-axis. As
${v_{\rm{D}}}$
and
${v_{\rm{C}}}$
increase, actors value the asset more and become more willing to fight.
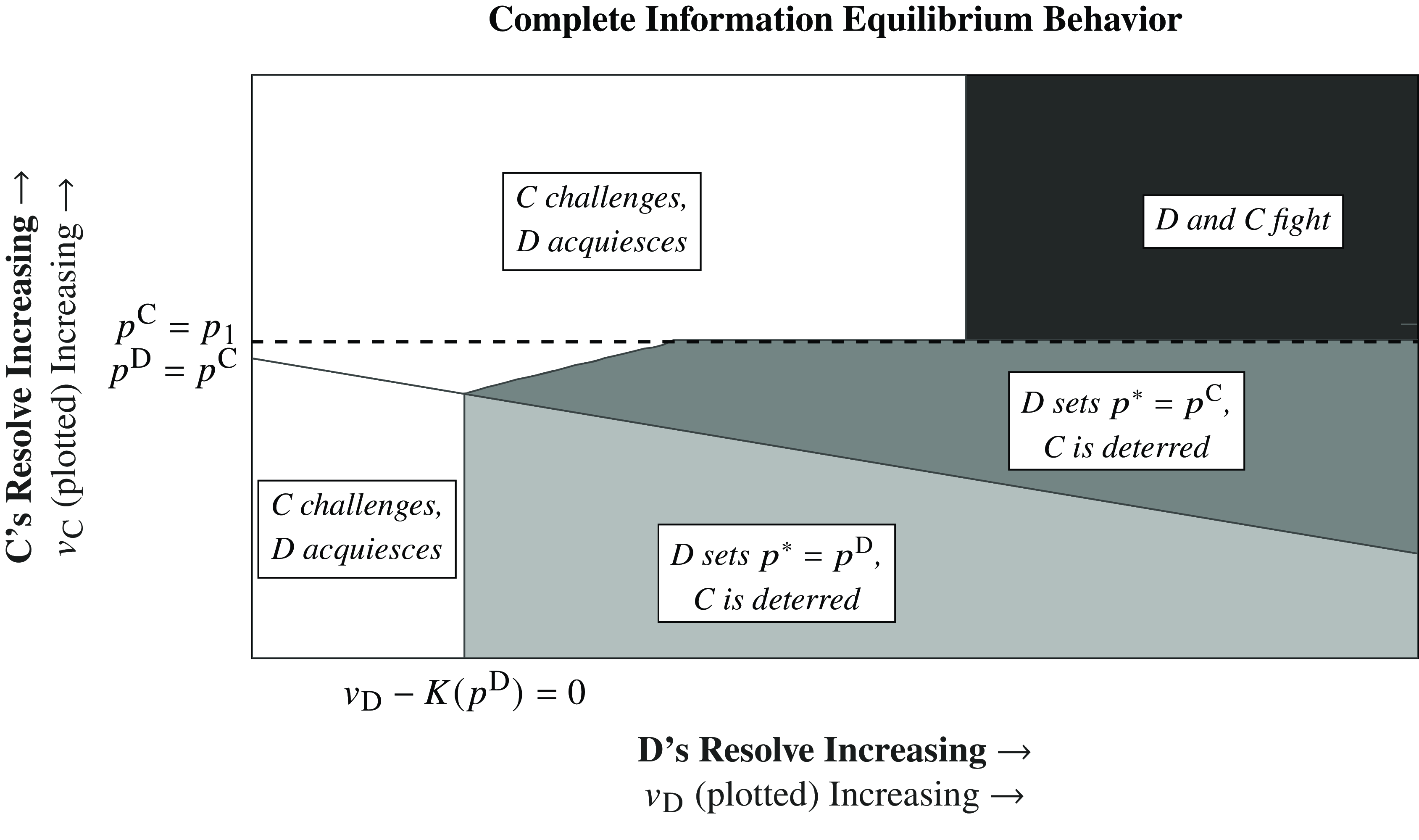
FIGURE 3. Equilibrium spaces in the complete-information deterrence game
Notes: For all white spaces, C will challenge and D will acquiesce. For all light-gray spaces, C will be deterred. And for all dark-gray spaces, C and D will fight.
First, consider the diagonal line labeled
${p^{\rm{D}}} = {p^{\rm{C}}}$
. For all values below this line,
${p^{\rm{C}}} \lt {p^{\rm{D}}}$
, meaning fighting is not possible, but deterring C is possible (case 3). For the lowest values of
${v_{\rm{D}}}$
(bottom left), D does not value the asset enough to arm to deter. Here D will set
${p^{\rm{*}}} = {p_0}$
, C will challenge, and D will acquiesce. Then, moving to the right, when
${v_{\rm{D}}}$
increases enough, D prefers arming to the level that will deter C from challenging to not arming and letting C have the asset; for all
${v_{\rm{D}}}$
values including and to the right of the
${v_{\rm{D}}} - K\left( {{p_{\rm{D}}}} \right) = 0$
cut-point, D will arm to level
${p^{\rm{*}}} = {p^{\rm{D}}}$
and deter C.
Next, consider the
${v_{\rm{C}}}$
and
${v_{\rm{D}}}$
values that fall above the
${p^{\rm{D}}} = {p^{\rm{C}}}$
line, where
${p^{\rm{D}}} \lt {p^{\rm{C}}}$
, but below the dotted
${p^{\rm{C}}} = {p_1}$
line, where
${p^{\rm{C}}} \lt {p_1}$
(case 1). Here D can arm with the intent of acquiescing, deterring, or fighting. When D does not value the asset much (low
${v_{\rm{D}}}$
), D will set
${p^{\rm{*}}} = {p_0}$
and acquiesce. And when D values the asset more, D will arm to level
${p^{\rm{*}}} = {p^{\rm{C}}}$
, which will deter C. In this region, for the selected parameters, D never prefers going to war.
Finally, consider the region above the dotted line labeled
${p^{\rm{C}}} = {p_1}$
, which is where
${p_1} \lt {p_{\rm{C}}}$
. For this region, C values the asset so highly that no feasible arming level will fully convince C not to fight—deterrence is not possible (Case 2). Thus D will either not arm and acquiesce (when
${v_{\rm{D}}}$
is lower), or arm in preparation for a fight (when
${v_{\rm{D}}}$
is higher).
In the next section, I discuss the general features of the equilibrium.
Results
Preliminaries
Before discussing the results, it is worthwhile describing how to practically interpret comparative statics on the parameter
$n$
. Most simply, the advent of nuclear weapons increased
$n$
. Before the nuclear era, competition and conflict between great powers carried no risk of an accidental nuclear launch because these weapons did not exist (
$n = 0$
); in the nuclear era, such risks now exist (
$n \gt 0$
). Furthermore, in the nuclear era, states that decentralize launch decisions, rely on potentially faulty automated systems for launch determination, or expand their nuclear arsenals (introducing more moving parts and opportunities for failure) heighten the nuclear risks of any conflict they become involved in.Footnote
45
Thus, changes in
$n$
can also approximate the changes that states make to their nuclear command-and-control infrastructure.
To further preview the analysis, the comparative statics in remarks 1, 2, and 5 depend on whether C’s war cost constraint binds (when
${p^{\rm{C}}} \gt {p^{\rm{D}}}$
) or D’s war participation constraint binds (when
${p^{\rm{C}}} \lt {p^{\rm{D}}}$
). Before discussing these remarks, it is worthwhile describing when, substantively, C’s war cost constraint would be expected to bind. This is perhaps clearest when, generally, both C and D place relatively high value on the asset. Given how the terms are defined, if D places a high value on the asset (high
${v_{\rm{D}}}$
), then
${p^{\rm{D}}}$
will be smaller; and if C places a high value on the asset (high
${v_{\rm{C}}}$
), then
${p^{\rm{C}}}$
will be greater. Thus, for jointly high-value assets, C’s war cost constraint is more likely to bind.Footnote
46
As an example, consider NATO as D, the Soviet Union as C, and West Germany as the high-value asset. NATO plausibly placed a high value on keeping West Germany outside of the Eastern Bloc, both for direct strategic reasons and to maintain the “status quo” of European borders.Footnote
47
And, plausibly, the Soviet Union also viewed West Germany as a high-value asset; in addition to the strategic value of expanding the Eastern Bloc, Stalin’s concerns over West Germany’s move into NATO and its rearmament could be addressed through the Soviet Union reunifying and controlling all of Germany.Footnote
48
Thus, in this example, the challenger’s (Soviet Union’s) war cost constraint would bind.
It is also useful to know when D’s war participation constraint would be expected to bind. This is clearest when both D and C place relatively low value on the asset (low
${v_{\rm{C}}}$
and
${v_{\rm{D}}}$
)—this lowers
${p^{\rm{C}}}$
and raises
${p^{\rm{D}}}$
, which together can imply that D’s war participation constraint is more likely to bind. Substantively, this could describe many Cold War crises that occurred in countries in regions that were, while still important, outside of the prioritized European theater.
Interestingly, in cases where one side places a high value on the asset and the other side places a low value on it, it is more difficult to determine whether
${p^{\rm{C}}}$
or
${p^{\rm{D}}}$
is bigger, which in turn makes understanding the effects of changes in
$n$
on outcomes more difficult.Footnote
49
And, naturally, these generalizations—like that D’s war participation constraint is more likely to bind when D and C care less about an asset—may break down when other features of conflict prove more influential.
Introducing Nuclear Risk May Require More or Less Conventional Arming for Deterrence
Introducing or increasing the unintended risk of nuclear escalation makes both C and D do worse should a conflict occur. This shapes force posture decisions.
Remark 1. Conventional forces and nuclear risks are imperfect substitutes. Formally, if
$n$
increases and D’s war participation constraint binds (
${p^{\rm{C}}} \lt {p^{\rm{D}}}$
), then D must increase its conventional force posture to maintain deterrence. Alternatively, if
$n$
increases and C’s war cost constraint binds (
${p^{\rm{C}}} \gt {p^{\rm{D}}}$
), then D can select a lower conventional force posture and still maintain deterrence.
Recall that for deterrence, both D’s war participation constraint and C’s war cost constraint must be met (formally, D must set
$p = {\rm{max}}\left\{ {{p^{\rm{C}}},{p^{\rm{D}}}} \right\}$
). Consider when D’s war participation constraint binds (
${p^{\rm{D}}} \gt {p^{\rm{C}}}$
). Here, to deter C, D must arm to the level where D is willing to fight. As nuclear instability increases, in order for D to continue being willing to fight, D must attain a better expected outcome when the conflict ends conventionally to compensate for the greater risk of a nuclear exchange. To achieve this better conflict outcome and maintain deterrence, D must select a greater initial force posture, or greater
$p$
.Footnote
50
Alternatively, consider when C’s war cost constraint binds (
${p^{\rm{D}}} \lt {p^{\rm{C}}}$
). Here, to deter C, D must arm to the level where C perceives war as unproductive. As the risk of nuclear escalation increases, C does worse in the conflict and wants to challenge less, meaning C will be deterred by a more limited conventional force posture, or lower
$p$
.Footnote
51
Thus, depending on which constraint binds, increasing nuclear instability could result in D needing greater or lower force postures for deterrence.
Of course, whether nuclear risk makes deterrence easier or harder—whether
${p^{\rm{C}}}$
is bigger than
${p^{\rm{D}}}$
or vice versa—can be substantively identified, as discussed earlier. If C and D both place relatively high value on the asset, then C’s war cost constraint is more likely to bind and added nuclear instability makes deterrence achievable at lower force postures. And, similarly, if C and D both place relatively low value on the asset, then D’s war participation constraint is more likely to bind, and added nuclear instability requires D to raise its conventional force posture for deterrence. Importantly, these results describe effects following changes in nuclear instability. They do not imply, for example, that D prefers crises when both
${v_{\rm{D}}}$
and
${v_{\rm{C}}}$
are high—deterrence is still easiest to achieve when
${v_{\rm{D}}}$
is high and
${v_{\rm{C}}}$
is low. Rather, remark 1 speaks to the marginal effect of nuclear instability on the level of arming needed for deterrence. Overall, remark 1 underscores the difficulty of replacing conventional deterrence capabilities with nuclear risk, especially for extended deterrence. Relying on nuclear risks in crises over non-existential issues introduces previously overlooked challenges. For example, Waltz claims that the catastrophic threat of nuclear retaliation clarifies confidence in deterrence, reducing the need for defenders to conduct large build-ups in conventional forces.Footnote
52
However, in crises where an intentional nuclear escalation is avoided, nuclear risks can undermine a defender’s willingness to fight, which can then be exploited by a challenger. In contrast to what is discussed by Waltz, this model suggests that the credibility problem in deterrence cannot be solved solely through threats of catastrophic outcomes and may also require a further commitment of conventional forces. After all, both challengers and defenders have agency in choosing whether to confront such risks; when nuclear risks are too high and conventional conflict outcomes are unfavorable, defenders may choose to disengage.
Welfare Effects When Conflict Does Not Occur
Increasing nuclear instability can impact overall ex ante welfare outside of changing how conflict plays out.
Remark 2. Increasing nuclear instability can either increase or decrease equilibrium conventional arming levels, thus raising or lowering overall ex ante welfare. Formally, suppose D deters C in equilibrium. If
$n$
increases and D’s war participation constraint binds (
${p^{\rm{C}}} \lt {p^{\rm{D}}}$
), then ex ante welfare decreases. But if
$n$
increases and C’s war cost constraint binds (
${p^{\rm{C}}} \gt {p^{\rm{D}}}$
), then ex ante welfare increases.
Consider what increasing nuclear instability means for welfare when D optimally deters C. As discussed in remark 1, as nuclear instability increases, D may select greater or lower force postures to deter C; in turn, this generates either greater or lower costs (respectively) for D to achieve the same deterrence outcome. Here, increasing nuclear instability can constitute a Pareto improvement when D can deter C by arming less, as can happen when D and C both place relatively high value on the asset (in other words, when C’s war cost constraint binds). And increasing nuclear instability can be Pareto-inefficient when D must arm more to deter C, as can happen when D and C both place relatively low value on the asset (when D’s war participation constraint binds).
Note that this observation is limited to how
$n$
affects force posture and welfare when D deters C in equilibrium. Outside of deterrence, the comparative statics become more complex. For example, suppose under some
$n$
D optimally deters C and
${p^{\rm{D}}} \gt {p^{\rm{C}}}$
. If
$n$
increases, D may not want to pay the higher costs to deter C any longer and may prefer to acquiesce; here increasing
$n$
would then decrease D’s arming level and could improve welfare.Footnote
53
To elaborate on these comparative statics, in the online supplement I discuss the general effects of changing
$n$
on arming and welfare.
This point has not been studied. In previous scholarship, nuclear optimists point to the decrease in great power conflict as a virtue of the nuclear era.Footnote 54 Meanwhile, nuclear pessimists typically note that, even if nuclear weapons reduce the likelihood of war, whenever war occurs it is more costly, as it bears the risk of a catastrophic nuclear exchange.Footnote 55 This trade-off—nuclear weapons mean fewer wars but introduce existential risks—has dominated the academic discourse.Footnote 56 Here I present a new trade-off to consider. In the nuclear era, while deterring direct threats to critical assets may be cheaper, establishing extended deterrence may necessitate more robust force postures, ultimately generating greater systemic costs.
Evidence of a Nuclear Peace
Consistent with the arguments of nuclear optimists and some empirical evidence,Footnote 57 my model suggests that introducing nuclear instability can lead to a more peaceful state of the world.
Remark 3. Increasing nuclear instability results in fewer instances of war. Formally, consider nuclear instability parameters
$n{\rm{'}},n{\rm{''}} \in {\mathbb{R}_ + }$
, with
$n{\rm{'}} \lt n{\rm{''}}$
. If
$n{\rm{'}}$
shifts to
$n{\rm{''}}$
, then the set of parameters where war occurs shrinks, and the likelihood of war decreases.
Moving from low to high nuclear instability will shrink the parameter set under which a conventional war will occur. To interpret this result, remark 3 implies that if we compared how history played out from 1950 to the present (
$n \gt 0$
) to a counterfactual history without the development of nuclear weapons (with
$n = 0$
), we would observe more conventional conflicts in the counterfactual history. Put simply, this model confirms that added nuclear instability lowers the likelihood of conventional war.
Two forces drive the nuclear peace. First, as nuclear instability increases, a conventional war becomes worse for the defender because the risk of nuclear escalation grows. Second, as nuclear instability increases, the set of possible force posture levels that could result in war—in other words, arming levels where C would be willing to challenge and D would be willing to escalate if challenged—is shrinking, potentially making deterrence cheaper. Thus, D will do worse from fighting a conventional war, and therefore will go to war less.Footnote 58 Note that this decrease in war arises either from D using its conventional force posture to deter C more frequently, or from D avoiding escalation more frequently (essentially accepting C’s fait accompli).
Figure 4 shows this visually. It includes three plots, each with fixed parameters (other than
$n$
). In the top plot,
$n = 0$
(there is no risk of a nuclear exchange), and there is a large range of values where the game ends in war. In the middle plot
$n = 0.03$
, and in the bottom plot
$n = 0.06$
. As
$n$
increases, the dark-gray region where war occurs shrinks, and the regions where D acquiesces and where D deters C grow.
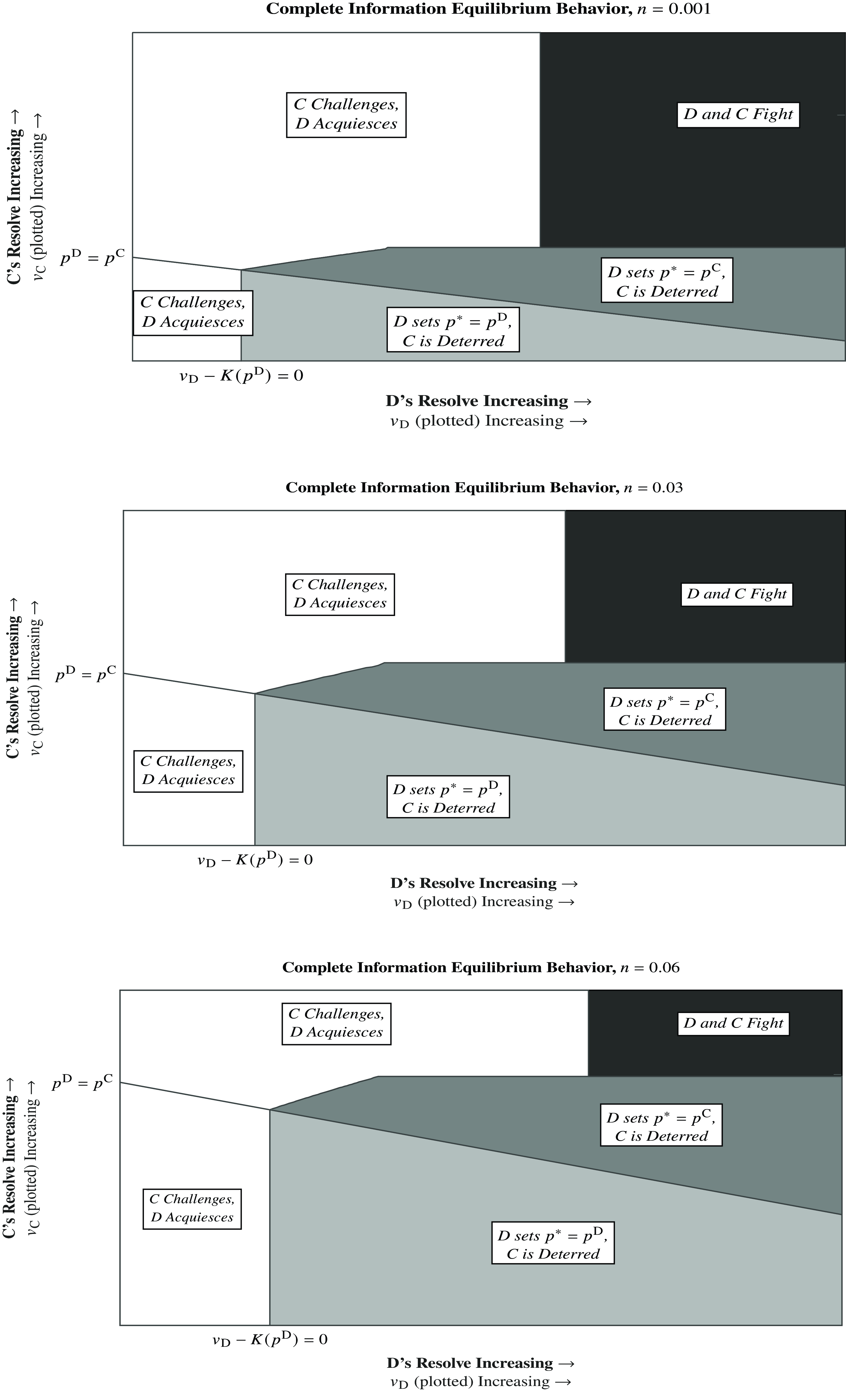
FIGURE 4. Equilibrium spaces in the complete-information deterrence game
Note: Instability parameter
$n$
increases from top to bottom.
Nuclear Instability and Arming Incentives
In the nuclear era, the defender seeks to avoid prolonged conflicts that carry a high risk of a nuclear exchange. To accomplish this, when it prepares for a fight, it may select a more aggressive or a less aggressive force deployment.
Remark 4. Under select conditions, as nuclear instability increases, D is incentivized to make conflict shorter and more decisive, and, to accomplish this, may select a more or a less aggressive force posture. Formally, assume the solution set to
$\hat p$
is a singleton set and both actors place high value on the issue.Footnote
59
Consider nuclear instability parameters
$n{\rm{'}}$
and
$n{\rm{''}}$
, where
$n{\rm{'}} \lt n{\rm{''}}$
. If
${p^{\rm{*}}}\left( {n{\rm{'}}} \right)$
is small enough, then
${p^{\rm{*}}}\left( {n{\rm{'}}} \right) \gt {p^{\rm{*}}}\left( {n{\rm{''}}} \right)$
. And if
${p^{\rm{*}}}\left( {n{\rm{'}}} \right)$
is large enough, then
${p^{\rm{*}}}\left( {n{\rm{'}}} \right) \lt {p^{\rm{*}}}\left( {n{\rm{''}}} \right)$
.
Figure 5 visualizes one version of remark 4. The left graph plots the equilibrium force posture (y-axis) for a range of
${v_{\rm{D}}}$
values (x-axis) where, for this set of parameters, C and D will fight in equilibrium. The dashed line plots the equilibrium force posture levels when the likelihood of a nuclear exchange is nonexistent (
$n = 0$
), and the solid line plots equilibrium force postures when nuclear instability is positive (
$n = 0.015$
). The right graph plots the expected time in conflict (y-axis) for the same
${v_{\rm{D}}}$
values (x-axis) and nuclear instability parameters.Footnote
60
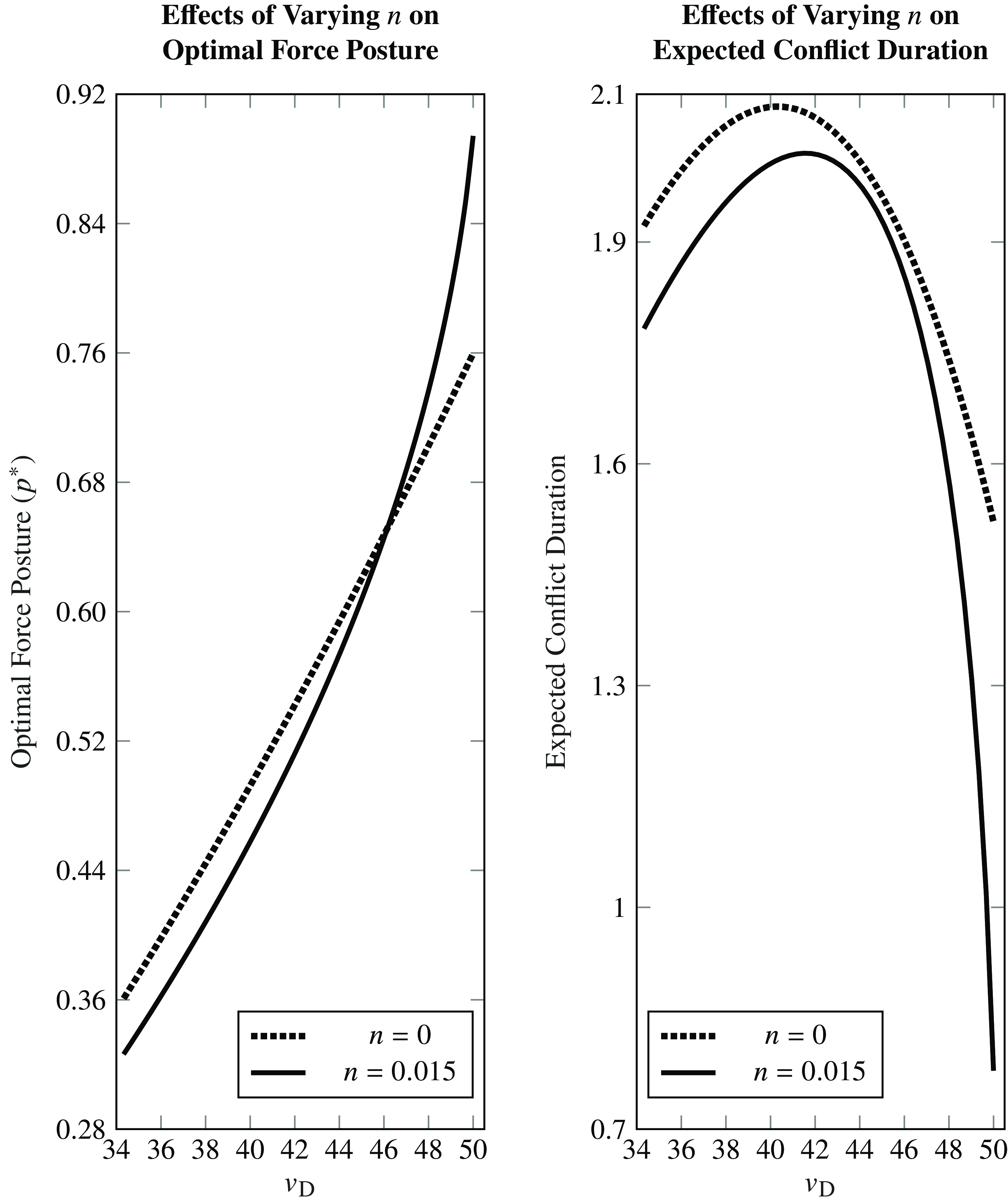
FIGURE 5. Optimal arming levels (y-axis, left) and expected conflict duration (y-axis, right) at different asset valuations (x-axis) for D at different levels of nuclear instability
Note: Increasing the nuclear instability parameter n from 0 to 0.015 can result in D arming less (for low
${v_D})$
or more (for high
${v_D}$
), leading to shorter conflicts in both cases under
$n = 0.015$
.
Consider the left plot in Figure 5. For the lowest
${v_{\rm{D}}}$
values (for example,
${v_{\rm{D}}} = 35$
), as
$n$
increases (moving from dashed to solid line), equilibrium arming levels decrease. In contrast, for the highest
${v_{\rm{D}}}$
values (for example,
${v_{\rm{D}}} = 49$
), as
$n$
increases, equilibrium arming levels increase. Thus, increasing the likelihood of a nuclear exchange has different effects on arming decisions, but these decisions are driven by the same underlying tensions. Recall how added force posture generates more nuclear risk when it makes the two sides more equal and less risk when it makes them less equal. Following that logic, for any initial arming level below
$p = 0.5$
for
$n = 0$
, adding nuclear risks presents new costs to staying in conflict, which incentivizes D to arm less to make conflict shorter (as it was in the
${v_{\rm{D}}} = 35$
example).Footnote
61
And similarly, for any initial arming level above
$p = 0.5$
for
$n = 0$
, adding nuclear risks presents new costs to staying in conflict, which now incentivizes D to arm more to make conflict shorter (as it was in the
${v_{\rm{D}}} = 49$
example). As we see in the right-hand plot, these different arming responses to the introduction of risk both work to shorten the expected conflict duration.
However, as remark 4 states (and the online supplement discusses further), the logic of the previous paragraph holds for large or small initial arming levels (that is, under
$n = 0$
). For initial arming values around
$0.5$
, competing effects can dominate arming decisions. In addition to introducing new costs to more prolonged conflicts, increasing
$n$
makes D’s arming less productive by decreasing the likelihood that D attains the asset, and increasing
$n$
mechanically shortens conflict duration, which in turn influences D’s anticipated conventional war costs. Furthermore, the marginal effects of changes in
$p$
on expected conflict duration are the smallest around
$p = 0.5$
, meaning D would be least willing to try to manipulate
$p$
to shorten conflict here. While at low or high initial arming values we would anticipate movement toward the extremes with increases in
$n$
, for intermediate values, comparative statics become more complex. This is visualized in the left-hand graph. For example, at
${v_{\rm{D}}} = 42$
, the arming level under
$n = 0$
is
${p^{\rm{*}}} \approx 0.54$
, and the arming level under
$n = 0.015$
is
${p^{\rm{*}}} \approx 0.52$
.
In line with the stability–instability paradox, Powell finds that strategic states always respond to greater nuclear instability with more restrained levels of force in conflicts, as was observed in the 1999 Kargil War.Footnote 62 The model here presents a new set of results. Under some parameters my results echo Powell, but at other times I find that defenders commit more force to a conflict when faced with greater nuclear instability and greater nuclear costs. Why? Here, unlike in Powell, the defender can avoid prolonged conflicts by reducing military parity through greater or lower levels of arming. While Powell argues that nuclear risk leads to reduced force deployments to minimize escalation, I find that conflicts with nuclear risks tend to be more decisive and shorter, potentially involving either more restrained or more aggressive force deployments to prevent escalation. This provides a theoretical basis for both restraint and excess in force deployment for conflict in the nuclear era, suggesting the stability–instability paradox may not be observed in cases where aggressive maneuvers can reduce escalation risks.
Deterrence Failure and Nuclear Instability
Remark 5. Increasing nuclear instability can increase or decrease the likelihood of deterrence failures. Formally, suppose D deters C in equilibrium and
${p^{\rm{D}}} \gt {p^{\rm{C}}}$
; if
$n$
increases, then the arming level required to deter C increases, and D may optimally switch to acquiescing. Now suppose D acquiesces to C in equilibrium and
${p^{\rm{D}}} \lt {p^{\rm{C}}}$
holds; if
$n$
increases, then the arming level required to deter C decreases, and D may optimally switch to arming up to the level that will deter C.
I define a deterrence failure as any equilibrium in which C challenges D. The frequency of these failures may rise or fall with increasing nuclear instability, driven by two competing effects.
First, suppose for a given
$n$
that D’s war participation constraint binds (
${p^{\rm{D}}} \gt {p^{\rm{C}}}$
). In this scenario, an increase in
$n$
makes D less willing to fight, raising the required arming level for deterrence,
${p^{\rm{D}}}$
. The increase in
${p^{\rm{D}}}$
could reach a point where D becomes unwilling to bear the cost of arming necessary to deter C’s challenge. If D opts not to deter C, then the rise in
$n$
results in a deterrence failure.
Second, suppose for a different set of parameters, C’s war cost constraint binds (
${p^{\rm{C}}} \gt {p^{\rm{D}}}$
). In some cases, D may initially be unwilling to arm to the level
${p^{\rm{C}}}$
required to deter C under low nuclear instability. However, increased nuclear instability reduces
${p^{\rm{C}}}$
, potentially making D willing to arm at the new, lower level and achieve deterrence. Ultimately, whether D experiences more or fewer deterrence failures following increases in nuclear instability depends on the underlying conditions of the case.
It is perhaps counterintuitive that when neither C nor D places high value on the asset (
${p^{\rm{C}}} \lt {p^{\rm{D}}}$
), deterrence failures are more common following increases in nuclear instability. Reasonable readers might ask why C would challenge over assets it does not value highly, especially in the face of increased nuclear instability. Ultimately, that intuition is incomplete because it does not take into account D’s agency and willingness to fight. To deter C from challenging, it is not enough for C to view war as prohibitively costly; D must also be willing to fight. If D places low value on the asset, then its willingness to fight becomes decisive, as C realizes it can challenge without triggering escalation. In this scenario, even though C places low value on the asset and recognizes that elevated
$n$
increases the risk of catastrophic outcomes in war, C also understands that higher
$n$
might altogether prevent D from engaging in a war, enabling C to seize the asset without escalation.
Empirical Implications
Asymmetric Response, Flexible Response, and the Value of Nuclear Instability
This model provides insights into the strengths and limitations of the “flexible response” and “asymmetric response” strategies. The first, adopted by the Kennedy administration, expanded US military capabilities to enable a broader range of responses to threats.Footnote
63
This expanded conventional force posture can be represented in model variations where force posture
$p$
is chosen from a broader set (when
${p_0} \approx 0$
and
${p_1} \approx 1$
). In equilibrium, if a defender can choose from a wide range of force levels, it will often do so, thus establishing deterrence across a range of different parameter values. Put another way, flexible response affords more opportunities for a defender to deter a challenger. However, flexible response cannot universally uphold deterrence. The model shows that deterrence can still fail—such as when both the challenger and defender value the asset highly (leading to war), or when only the challenger does (causing the defender to acquiesce when challenged). Ultimately, actors’ underlying preferences—how much each side values the asset—remain crucial in determining whether deterrence succeeds or fails, even with flexible force posture options.
To assess the effectiveness of flexible response, we can compare it to its predecessor, the Eisenhower administration’s asymmetric-response strategy, which prioritized nuclear threats or first use over conventional responses to international threats.Footnote
64
Since asymmetric response minimized the development of conventional forces, this doctrine can be represented formally by a lower and narrower range of force postures—that is, a lower
${p_1}$
when compared to the broader range in flexible response. With the narrower range of force postures, deterrence under asymmetric response would fail under more settings when compared to flexible response. Deterrence may break down if the challenger cannot implement the force posture necessary to deter the challenger (whenever
${p_1} \lt {p_{\rm{C}}}$
), or if fighting becomes less advantageous for the defender (because D’s utility from fighting is decreasing in
${p_1}$
). In this setting, the restricted conventional force posture of asymmetric response weakens deterrence.
Understanding how the advent of nuclear weapons shaped Cold War deterrence strategies is also crucial. Remarks 1, 2, and 5 suggest that the development of these weapons (moving from zero to positive levels of nuclear instability) made deterrence easier, more cost effective and less likely to fail when both challenger and defender place relatively higher value on the asset (resulting in
${p_{\rm{C}}} \gt {p_{\rm{D}}}$
). Substantively, this could describe the case of Western Germany, especially West Berlin, which was of central concern to both the US and the Soviet Union.Footnote
65
This theory supports claims that, for much of the Cold War, territories like West Berlin were vulnerable to a Soviet invasion, but nuclear risk strengthened Western deterrence.Footnote
66
Put another way, in a counterfactual world where nuclear weapons had never been created, the West would have needed a relatively larger and costlier conventional force posture to deter the Soviet Union from invading Germany.
But remarks 1, 2, and 5 also suggest that the advent of nuclear weapons can make deterrence harder, in settings where both challengers and defenders place relatively lower value on the asset (resulting in
${p_{\rm{D}}} \gt {p_{\rm{C}}}$
). Substantively, this could describe settings outside of the strategically prioritized European theater, like in Latin America, Africa, and Asia. Consider, for example, what this theory means for the US decision not to use tactical nuclear weapons during the Vietnam War. While multiple factors can explain the nonuse of nuclear weapons,Footnote
67
these results emphasize a potential strategic tension. Deploying tactical nuclear weapons raises the risk of escalation to a strategic nuclear exchange (
$n$
). Using tactical nuclear weapons might have then, perversely, required the US to commit even more conventional forces to remain willing to fight under the elevated nuclear risks—a step the US was likely hesitant to take. In other words, the US might not have been willing to fight the Vietnam War if it carried a higher risk of escalation to a strategic nuclear exchange, which could explain its reluctance to deploy tactical nuclear weapons and raise those escalation risks. While the US ultimately failed to re-establish deterrence in South Vietnam, using tactical nuclear weapons could have proven strategically counterproductive.
These dynamics—whether added nuclear risk raises or lowers the conventional force posture needed for deterrence—relate to the asymmetric-response and flexible-response doctrines. Consider the possibility that the asymmetric-response strategy not only lowered
${p_1}$
(as just discussed) but also increased nuclear instability (higher
$n$
).Footnote
68
The added nuclear risk under asymmetric response could have proven counterproductive. When both sides place low value on the asset (
${p_{\rm{D}}} \gt {p_{\rm{C}}}$
), higher nuclear instability requires increasing arming levels for deterrence, raising the costs for deterrence or making deterrence infeasible under asymmetric response.Footnote
69
Conversely, when both sides place high value on the asset (
${p_{\rm{C}}} \gt {p_{\rm{D}}}$
), even if a higher level of nuclear instability reduces the arming level needed to deter C, C’s high valuation means that the conventional arming requirement for deterrence would be high regardless; because asymmetric response limits the available conventional force posture, raising nuclear instability may not be enough to deter a challenger when the defender’s conventional options are limited.Footnote
70
In contrast, because flexible response still maintains a wide range of possible conventional force postures, in many cases, it can still uphold deterrence at the lower nuclear instability levels.
Of course, the comparison between flexible response and asymmetric response comes with caveats. This model best describes cases where the asset is important but not existentially important, which, based on past critiques of the asymmetric-response strategy, is where asymmetric response would be expected to perform worst. Ultimately, generalization of this evaluation of the doctrines under a broader set of assumptions is needed.
Nuclear Risk and Force Postures: The Hungarian Revolution and Kashmir in 2019
In late October 1956, Budapest was in crisis. Following a series of clashes between student protesters and government forces, a group of anti-Soviet revolutionaries ousted or killed a critical mass of Hungarian communist leaders and members of the Hungarian secret police, eventually (on October 27) installing Imre Nagy as prime minister. At first Soviet leadership considered negotiating with Nagy and the new Hungarian government, but after several days they changed course and invaded Hungary. By 3 November, Operation Whirlwind was underway; 30,000 Soviet troops invaded Hungary and circled Budapest.Footnote 71 Eight days later, Soviet forces decisively defeated the revolutionaries, deposed the revolutionary government, and resumed control of Hungary.
In the broader Cold War context, the Soviet activities in Hungary were not without international risks. Until that point, the Eisenhower administration had publicly advocated the “rolling back” of Soviet influence in Eastern Europe, even if it required using armed forces.Footnote 72 In fact, Soviet leadership acknowledged that the crisis in Hungary had international dimensions, believing it could spread to other Soviet states and perhaps lead to a confrontation with the West.Footnote 73 But these escalation risks did not convince the Soviet Union to apply restraint; instead, it acted aggressively and crushed the revolution. Why?
Before analyzing the events, it is worthwhile grounding the case in the model’s terms. The Hungarian Revolution presented the US and the Soviet Union with a crisis that could have escalated into a general war with nuclear risk.Footnote 74 I treat the Soviet Union as the model’s “defender” (defending the pre-revolution status quo in Hungary), and the West as the “challenger,” who could have backed the Hungarian revolutionaries. The Soviet Union achieved the decisive outcome it did by putting forward a strong conventional force deployment. And in response to the Soviet Union’s force posture, the United States had a choice: to challenge and support the revolution, or to stay back.
The model presented here can offer insight into the Soviet Union’s robust response. The Soviet Union’s conventional force posture in Eastern Europe and the significant forces deployed to quell the Hungarian Revolution all but guaranteed that the Soviet Union would do well should the crisis escalate into a conflict with the West—essentially, the Soviets had selected a high
$p$
. This meant that the West would likely be deterred from escalating this crisis, but even if it was not deterred, Soviet conventional forces could plausibly end a US challenge quickly enough. To explain this aggressive force posture, consider the implications of remark 4: the nuclear risk may have incentivized the Soviet Union to adopt a more aggressive conventional force posture than it otherwise might have. By acting decisively to end the crisis quickly, the Soviet Union sought to avoid a protracted conflict that could accidentally or inadvertently escalate to a nuclear exchange, at the expense of the Hungarian revolutionaries and public. While caveats naturally apply here—there are many reasons to end a revolution quickly—the benefits of decisive action were not lost on Khrushchev. As we now know, after the invasion, when his son asked why the Americans had not intervened with military force in Hungary, Khrushchev replied that “everything happened so quickly that possibly they simply did not have time to do so.”Footnote
75
Furthermore, the Hungarian Revolution is not the only time that a nuclear-armed state acted decisively while negotiating a crisis with another nuclear-armed state. For the past several decades, India and Pakistan have periodically clashed over disputed territory in the Kashmir region, including during the Kargil War of 1999. Then, in 2019, the government of India abrogated Article 370 of the Indian constitution and passed the Jammu and Kashmir Reorganization Bill, which together dramatically altered the status of the Kashmir territory currently administered by India.Footnote 76 New Delhi’s actions eliminated Jammu and Kashmir’s special status as a fairly autonomous Indian state, dismantled its existing institutions and laws, and placed it under the Union government’s overarching control. While these abrupt political changes to the contested (and recently fought-over) region heightened tensions between India and Pakistan, in preparation for any potential challenges, New Delhi sent between 40,000 and 45,000 additional soldiers and police to Jammu and Kashmir, bringing the number of Indian troops in the region to approximately 100,000,Footnote 77 locked down mobile and internet communications, and rolled out extensive and protracted curfews.
This dramatic policy shift inflamed tensions in a long-simmering regional conflict that has been punctuated by both direct military confrontation and third-party-backed terrorist attacks. While we do not have access to the deliberations of Narendra Modi and his inner circle, it is reasonable to assume that they believed that Pakistan would challenge the abrogation, potentially through conflict. In the past, Pakistan’s Inter-Services Intelligence has backed terrorist groups that have conducted attacks over less dramatic changes to Kashmir’s politics.Footnote 78 And in the weeks after India’s actions, Imran Khan publicly threatened a confrontation, saying in a televised address, “Whether the world joins us or not, Pakistan will go to any lengths and its people will support [Kashmiris] till their last breath.”Footnote 79 While past behavior or messaging may not be predictive of behavior in a crisis, after the abrogation, scholars and policy makers suggested that Pakistan might respond by supporting terrorists or issuing nuclear threats.Footnote 80
While Pakistan’s challenging the abrogation was a possibility, after India flooded Jammu and Kashmir with security forces, Pakistan’s options were limited. Pakistan would struggle to directly confront India in Kashmir. Pressed by hawkish opposition members in Parliament to respond to India’s actions, Khan replied incredulously, “What do you want me to do … Should I go to war with India?”Footnote 81 Pakistan’s more common response of supporting militant groups in Kashmir also seemed likely to fail. Given the concentration of security forces, militant or terrorist attacks seemed unlikely to dislodge the Indian forces or change the political situation. All together, India’s force deployment suggested a readiness to quickly address any challenge that Pakistan presented. Consistent with remark 4, the nuclear risks plausibly motivated India to act more decisively than it would have in a nonnuclear scenario, resulting in a quick resolution to the crisis and minimal escalation risks.
Additional Results and Extensions
Here I consider several extensions to the model and the analysis.
Making n Endogenous
In some circumstances, the defender may be able to manipulate the level of nuclear risk. A modified version of the game, discussed in the online supplement, explores this prospect. The key change is that as the defender selects its arming level, it can also costlessly select some level of nuclear instability,
${n_{\rm{D}}}$
. For this across-game-form analysis to be informative,Footnote
82
I assume that D selects
${n_{\rm{D}}}$
from a compact subset of
${\mathbb{R}^1}$
that contains
$n$
, where
$n$
is the nuclear-instability parameter from the original game form.
In the equilibrium, sometimes D will select more nuclear instability (
${n_{\rm{D}}} \gt n$
), and other times less nuclear instability (
${n_{\rm{D}}} \lt n$
). Why? If C’s war cost constraint binds, then by selecting some
${n_{\rm{D}}} \gt n$
, D can deter C at a lower conventional force posture and at lower cost. On the other hand, if D’s war participation constraint binds, then by selecting some
${n_{\rm{D}}} \lt n$
, D becomes more willing to fight when challenged, which allows D to establish deterrence at a lower force posture. Thus, granting D the option to manipulate nuclear instability levels will expand the parameter range where D can deter C.
Bargaining
The model in the main text was a deterrence model, like the paper this model is closest to.Footnote 83 However, some readers may have concerns about the absence of bargaining. Ultimately, if the crisis-bargaining setting also has some kind of commitment problem, then the deterrence setting can resemble the crisis-bargaining setting.Footnote 84 In the online supplement, I modify the model to (a) allow for endogenous bargaining and (b) have a commitment problem stemming from a power shift. I find that while the crisis-bargaining model with commitment problems presents new scope conditions under which fighting is possible, the results are largely the same.
Extension: Incomplete-Information Game
Model and equilibrium intuition
I also analyze a version of the game with incomplete information. Its form is nearly identical to the one described earlier, only here, before D selects its conventional force level, nature sets D’s resolve (how much D cares about the issue) as low or high. Formally, nature sets
${v_{\rm{D}}} \in \left\{ {{{\underline v }_{\rm{D}}},{{\bar v}_{\rm{D}}}} \right\}$
, with
$0 \lt {\underline v _{\rm{D}}} \lt {\bar v_{\rm{D}}}$
. I let
$\pi \in \left( {0,1} \right)$
denote the probability that D is type
${\bar v_{\rm{D}}}$
, and
$1 - \pi $
that it is type
${\underline v _{\rm{D}}}$
. D knows its type, but C does not. In this game, I limit analysis to an essentially unique perfect Bayesian Nash equilibrium that satisfies the intuitive criterion.Footnote
85
I summarize the key points here, and offer a full discussion in the online supplement.
In the incomplete-information game, there is a new strategic tension: C is uncertain of D’s resolve, and thus sometimes uncertain whether D is willing to fight. This in turn can shape D’s force posture decisions in new ways, leading to bluffing or signaling (as we will see). But the incomplete-information assumption does not change the game everywhere, and much of the behavior is similar to the complete-information game: sometimes different types of D will (still) acquiesce, deter, or fight.
I depict the equilibrium spaces in Figure 6. Here
${\underline v _{\rm{D}}}$
varies on the x-axis, and
${v_{\rm{C}}}$
on the y-axis, while other parameters are fixed. The text boxes describe how type
${\bar v_{\rm{D}}}$
behaves, then how type
${\underline v _{\rm{D}}}$
behaves, in each parameter space. A range of equilibrium behavior can be supported. For the highest values of
${\underline v _{\rm{D}}}$
and
${v_{\rm{C}}}$
, both types of D will always go to war. For the lowest values of
${\underline v _{\rm{D}}}$
and
${v_{\rm{C}}}$
, sometimes low-resolve defenders will drop out and acquiesce, while high-resolve defenders deter C. Other times, low-resolve defenders will mimic a high-resolve defender’s force posture to convince C to not challenge, despite their being unwilling to fight at that force posture (that is, they bluff). Other times, high-resolve defenders will select a high-enough force posture to get low-resolve defenders to stop mimicking them, effectively “over-arming” to demonstrate that they are resolved types, which keeps C from challenging (that is, they signal). In the remaining spaces, deterrence, acquiescing, and fighting largely play out as they do in the complete-information model, though here sometimes different types behave differently (see the online supplement for full details).
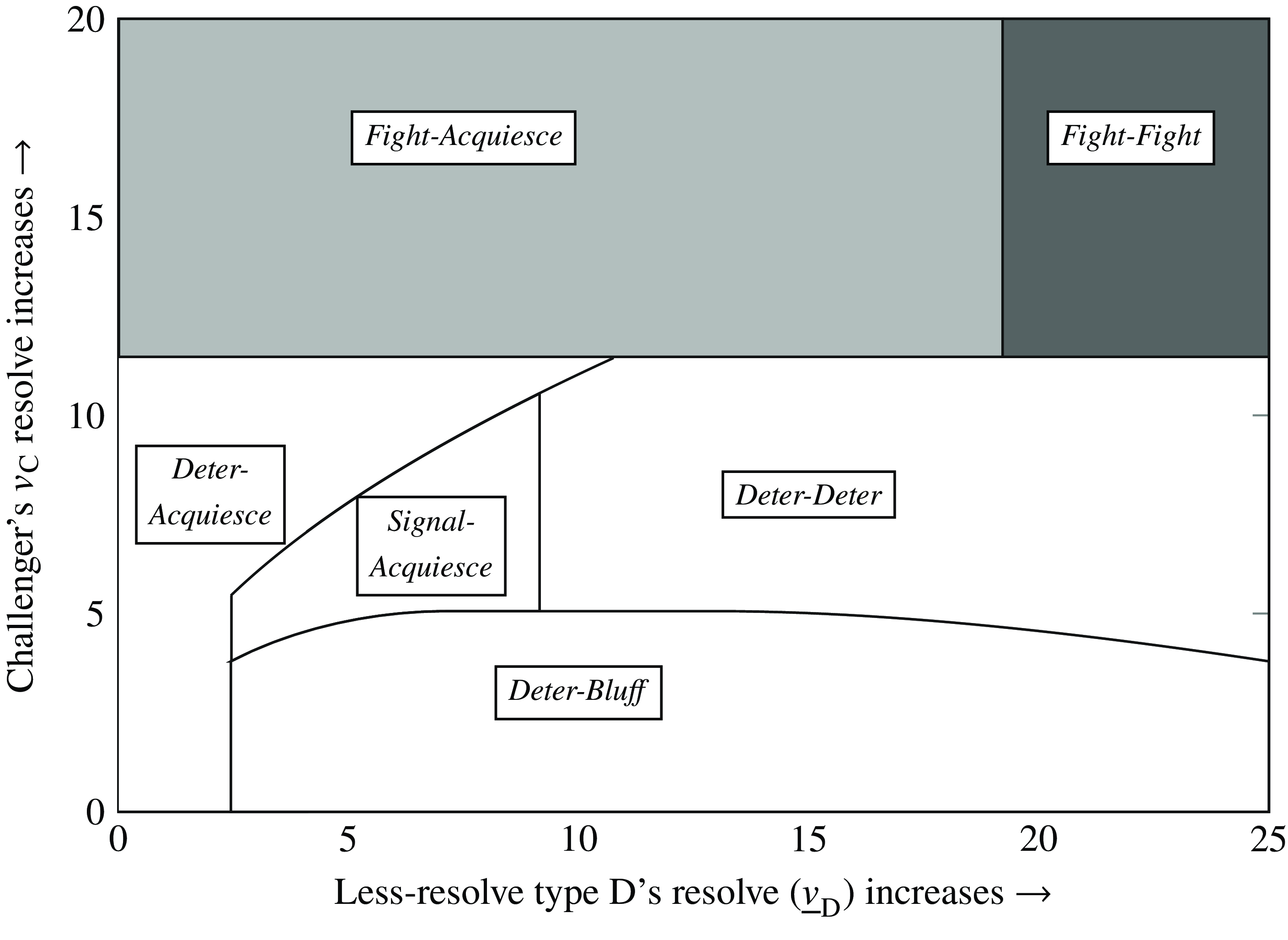
FIGURE 6. Equilibrium spaces in the incomplete-information game
Notes: The x-axis varies
${\underline v _{\rm{D}}}$
, which is the less-resolve type’s valuation of the asset, and the y-axis varies
${v_C}$
, which is the challenger’s valuation of the asset. The darkness of shading represents the likelihood of war. In the white equilibrium spaces, war never occurs. In the light-gray Fight-Acquiesce equilibrium space, war occurs when D is type
${\bar v_D}$
. In the dark-gray Fight-Fight equilibrium space, war always occurs.
Results
Adding incomplete information to the complete-information model is a natural modification: actors plausibly may not know how much their opponent cares about the issue at stake.Footnote 86 But this model modification does not change any of the earlier remarks.
Remark 6 is a useful robustness check. Actors play different kinds of equilibrium strategies in the different versions of the model (complete versus incomplete information). Despite this, remark 6 implies that remarks 1 to 5 can also apply to settings where the degree of resolve is unknown, thus expanding the real-world applicability of these results.
The incomplete-information model can also generate new results. The model with private resolve here works differently from Powell’s model with private resolve.Footnote 87 Here it is possible for the defender to signal its private resolve without ever having to go to war.
Remark 7. Peaceful signaling of resolve is possible.
High-resolve defenders signal their high resolve by arming beyond the level needed to make themselves willing to fight. Essentially, they must arm to a level low-resolve defenders would not be willing to match (due to the cost). This is
$\bar p$
.Footnote
88
As a result, in equilibrium, only a high-resolve D will arm to level
$\bar p$
; C knows on seeing
$p = \bar p$
that D is resolved and would fight if challenged, and C will never challenge.Footnote
89
Within the parameter set where D signals, arming as a costly signal of resolve always works, in that high-resolve defenders can always achieve peace through deterrence.
In Powell’s work, signaling functions differently. There, manipulating nuclear risk—which is how the defender signals its resolve—is costless unless a conventional war breaks out. And, following the standard signaling logic, unless the signal is costly, low-resolve types are incentivized to mimic high-resolve types, undermining the informative value of the signal. As a result, for Powell, the defender can signal its resolve only by sometimes actually going to war because the signal generates costs only through war.
This distinction has real-world implications. My model suggests that resolved defenders can deter challengers and prevent conflict through the costly signal of a robust conventional force posture. In contrast, Powell finds that resolved defenders cannot fully deter challengers by manipulating nuclear risk, so conflict must sometimes occur as part of a costly signaling mechanism. There are two ways to interpret these results. First, I am presenting a more optimistic perspective. For Powell, war is an inevitable part of the signaling of resolve, whereas I find it is possible to signal resolve and deter an opponent without resorting to conflict. Second, from a practical perspective, if a defender wants to signal resolve and avoid conflict, that defender should signal by manipulating force posture rather than manipulating nuclear risk (as Powell would have it).
Conclusion
The advent and proliferation of nuclear weapons have introduced a disturbing reality: conventional conflicts between great powers now carry the risk of accidentally escalating into a catastrophic nuclear exchange.Footnote 90 The magnitude of this risk has profoundly shaped deterrence and conflict dynamics in the nuclear era. This paper examines these dynamics in the context of crises over non-existential issues.
My most novel finding is that, within such conflicts, leveraging nuclear risks only sometimes supports deterrence. For conventional deterrence to hold, a defender must be willing to fight if challenged, and the cost of fighting must be high enough to dissuade the challenger.
When deterrence depends on imposing costs on a challenger—meaning the defender is already motivated to fight—increased nuclear risk makes conventional conflict more costly for the challenger, strengthening the defender’s deterrent threat. But when deterrence depends on the defender’s willingness to respond to a challenge, increased nuclear risk makes conventional conflict more costly for the defender, undermining the defender’s credibility. This latter result—that the nuclear revolution may require expanded conventional force postures for deterrence—suggests that the nuclear revolution may result in additional challenges to extended deterrence, more costly and expansive force postures, and more deterrence failures. While much attention has been paid to the underlying risks of nuclear weapons,Footnote 91 my model suggests that nuclear weapons may reduce welfare through other channels as well.
It also offers a new perspective on conflict in the nuclear era, suggesting it is not solely an era of restraint and limited wars but also one of aggression, where actors adopt robust conventional force postures in order to shorten conflicts. This formal result is new, and arises from bridging two previously unrelated strands of research: research on conventional capabilities and conflict duration, and research on how nuclear risk is generated.
And finally, it suggests some normative benefit of the nuclear era: the observed “long peace” could be a “nuclear peace,” where the nuclear great powers are less willing to engage in protracted conventional wars and more willing to engage in more decisive, shorter contests with reduced risk of nuclear escalation.
Future research should continue examining these under-formalized topics. Moving forward, war should not be treated as a game-ending move with a specific functional form. One way to move forward would be to treat war as a continuous-time process, where states can “drop out” at any time. Indeed, the setup given here would lend itself to that, with
$n$
and
${\alpha \over {p\left( {1 - p} \right)}}$
being used as hazard rates for the conflict ending via a nuclear exchange or a conventional victory, respectively. Alternatively, the functional forms for conflict could be generalized; for example, future iterations could consider risks from both the scope of the initial confrontation and time in conflict. Beyond these cases, “gray-zone conflict,” where adversaries target low-value assets with limited capabilities,Footnote
92
warrants further study on how the evolving nuclear landscape might shape its dynamics.
Supplementary Material
Supplementary material for this article is available at <https://doi.org/10.1017/S0020818325000025>.
Acknowledgments
I thank Brad Smith, Brenton Kenkel, Andrew Coe, Peter Bils, Jennifer Larson, Andres Gannon, Ethan Bueno de Mesquita, James Morrow, Andrew Kydd, Alex Debs, Robert Gullotti, Erik Gartzke, Thomas Schere, Scott Tyson, Jessica Sun, Josh Clinton, Brett Benson, and three anonymous reviewers for their thoughts and guidance. I’d like to especially thank James Fearon for encouraging this project and his willingness to read and comment on multiple drafts. Thanks also to seminar participants at the Center for Peace and Security Studies, the Midwest Political Science Association’s annual conference, and the Pittsburgh Formal Theory Conference for their helpful advice. The views, analyses, and conclusions expressed in this article are those of the author. Any errors or omissions are the author’s responsibility.
