No CrossRef data available.
Published online by Cambridge University Press: 12 April 2016
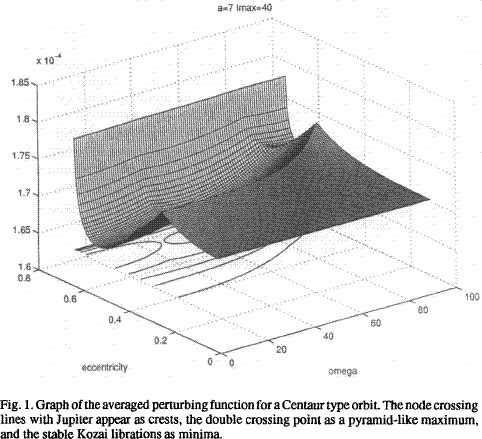
The orbits of planet-crossing asteroids (and comets) can undergo close approaches and collisions with some major planet. This introduces a singularity in the N-body Hamiltonian, and the averaging of the equations of motion, traditionally used to compute secular perturbations, is undefined. We have shown (Gronchi and Milani, 1998) that it is possible to define in a rigorous way some generalised averaged equations of motion, in such a way that the generalised solutions are unique and piecewise smooth, with corners on the node crossing lines.
The model is the averaged equations of motion first introduced by Kozai (1962): the perturbing planets are assumed to move in circular, coplanar orbits, and the equations of motion are averaged over the anomalies of the asteroid and of the planets. In the non-crossing case the averaging is integrable; in the planet-crossing case there is a polar singularity of order two in the equations of motion, and averaging is not possible. To define a generalized solution, we decrease the order of the polar singularity by the method of extraction of the singularities by Kantorovich. The singularity of the perturbing function is approximated by a modified inverse distance, the one between the straight lines tangent to the two orbits at the nodal points. In this approximation the averaged perturbing function has an analytical expression, allowing explicit computation with elliptic integrals and elementary functions.