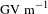1 Introduction
Ion beams generated via the target normal sheath acceleration (TNSA) mechanism posses remarkable characteristics such as high particle flux, ultra-low emittance and short pulse duration, but also exhibit large envelope divergence and broad energy distribution[Reference Macchi, Borghesi and Passoni1]. Although the two latter properties are advantageous in plasma radiography applications[Reference Borghesi, Campbell, Schiavi, Haines, Willi, MacKinnon, Patel, Gizzi, Galimberti, Clarke, Pegoraro, Ruhl and Bulanov2–Reference Kar, Borghesi, Audebert, Benuzzi-Mounaix, Boehly, Hicks, Koenig, Lancaster, Lepape, Mackinnon, Norreys, Patel and Romagnani6], these are generally undesirable in view of many other potential applications[Reference Bulanov and Esirkepov7, Reference Patel, Mackinnon, Key, Cowan, Foord, Allen, Price, Ruhl, Springer and Stephens8]. Therefore controlling and optimising the laser driven ion beam parameters has been one of the intensively studied research topic over the past decade[Reference Patel, Mackinnon, Key, Cowan, Foord, Allen, Price, Ruhl, Springer and Stephens8–Reference Kar, Markey, Simpson, Bellei, Green, Nagel, Kneip, Carroll, Dromey, Willingale, Clark, McKenna, Najmudin, Krushelnick, Norreys, Clarke, Neely, Borghesi and Zepf13].

Figure 1. (a) shows a schematic of the experimental setup for transverse proton probing of the EM pulse propagating along a helical coil (not to scale). (b) Shows the front view (looking from the detector side) of the target. (c) and (d) Show the radiographs of the helical coil obtained by 5.5 and 3.0 MeV protons, respectively. The dotted lines show the axes of the proton beam and the intersection point is the approximate centre of the proton beam. The spatial scale shown in (c) corresponds to the image plane.
TNSA-driven proton beams have been extensively used as a radiographic tool to study the dynamics of electric and magnetic fields generated by intense laser interactions[Reference Borghesi, Campbell, Schiavi, Haines, Willi, MacKinnon, Patel, Gizzi, Galimberti, Clarke, Pegoraro, Ruhl and Bulanov2–Reference Ahmed, Dieckmann, Romagnani, Doria, Sarri, Cerchez, Ianni, Kourakis, Giesecke, Notley, Prasad, Quinn, Willi and Borghesi5]. The emission of an ultra-short burst of protons with a broad energy spectrum from a point-like source allows the implementation of point-projection probing schemes, while providing multi-frame snapshots of the probed object. The ultra-short burst duration enables a high temporal resolution (typically of a few ps), while the beam laminarity and small source size ensures a high spatial resolution[Reference Borghesi, Mackinnon, Campbell, Hicks, Kar, Patel, Price, Romagnani, Schiavi and Willi14, Reference Cowan, Fuchs, Ruhl, Kemp, Audebert, Roth, Stephens, Barton, Blazevic, Brambrink, Cobble, Fernandez, Gauthier, Geissel, Hegelich, Kaae, Karsch, Le Sage, Letzring, Manclossi, Meyroneinc, Newkirk, Pepin and Renard-LeGalloudec15].
The propagation of an electromagnetic (EM) pulse generated by intense laser interaction with a solid target was recently studied by employing a self-probing arrangement[Reference Kar, Ahmed, Prasad, Cerchez, Brauckmann, Aurand, Cantono, Hadjisolomou, Lewis, Macchi, Nersisyan, Robinson, Schroer, Swantusch, Zepf, Willi and Borghesi16–Reference Kar, Ahmed, Nersisyan, Brauckmann, Hanton, Giesecke, Naughton, Willi, Lewis and Borghesi18]. The ultra-short EM pulses with peak electric field of the order of
![]() $10^{9}~\text{V}~\text{m}^{-1}$
, are generated following the rapid charging of the laser-irradiated target to MV potential, due to the prompt escape of the high energy (MeV) electrons produced during the interaction[Reference Borghesi, Campbell, Schiavi, Haines, Willi, MacKinnon, Patel, Gizzi, Galimberti, Clarke, Pegoraro, Ruhl and Bulanov2, Reference Kar, Markey, Simpson, Bellei, Green, Nagel, Kneip, Carroll, Dromey, Willingale, Clark, McKenna, Najmudin, Krushelnick, Norreys, Clarke, Neely, Borghesi and Zepf13, Reference Poye, Dubois, Lubrano-Lavaderci, Humieres, Bardon, Hulin, Bailly-Grandvaux, Ribolzi, Raffestin, Santos, Nicolai and Tikhonchuk19]. The EM pulse was observed propagating along a thin metallic wire attached to the main foil target. In this case the pulse-carrying wire was shaped into a square wave pattern contained in a plane perpendicular to the axis of the probe proton beam.
$10^{9}~\text{V}~\text{m}^{-1}$
, are generated following the rapid charging of the laser-irradiated target to MV potential, due to the prompt escape of the high energy (MeV) electrons produced during the interaction[Reference Borghesi, Campbell, Schiavi, Haines, Willi, MacKinnon, Patel, Gizzi, Galimberti, Clarke, Pegoraro, Ruhl and Bulanov2, Reference Kar, Markey, Simpson, Bellei, Green, Nagel, Kneip, Carroll, Dromey, Willingale, Clark, McKenna, Najmudin, Krushelnick, Norreys, Clarke, Neely, Borghesi and Zepf13, Reference Poye, Dubois, Lubrano-Lavaderci, Humieres, Bardon, Hulin, Bailly-Grandvaux, Ribolzi, Raffestin, Santos, Nicolai and Tikhonchuk19]. The EM pulse was observed propagating along a thin metallic wire attached to the main foil target. In this case the pulse-carrying wire was shaped into a square wave pattern contained in a plane perpendicular to the axis of the probe proton beam.
It has been shown recently[Reference Kar, Ahmed, Prasad, Cerchez, Brauckmann, Aurand, Cantono, Hadjisolomou, Lewis, Macchi, Nersisyan, Robinson, Schroer, Swantusch, Zepf, Willi and Borghesi16] that, by directing such a high amplitude EM pulse in a helical path around the proton beam, the spectral and angular properties of the beam can be controlled and optimized. This motivates the study of the propagation of the EM pulse in a helical geometry, which is presented in this paper. By following the spatial and temporal evolution of the electric field across the helical coil, probed transversely by the probe protons, the pulse profile was reconstructed with the help of particle tracing simulation. The characteristic parameters of the pulse, such as duration and amplitude, are broadly in agreement with those obtained previously in a planar probing geometry and similar interaction condition[Reference Ahmed, Kar, Cantono, Nersisyan, Brauckmann, Doria, Gwynne, Macchi, Naughton, Willi, Lewis and Borghesi17]. The effect of the EM pulse on the proton beam travelling through the helical coil was studied by probing a short helical coil longitudinally. Particle tracing simulations were employed to model this process, which are in agreement with the reduction in beam divergence observed for protons of a small energy range, travelling in synchronisation with the EM pulse. Furthermore, it is shown that the beam collimation is dramatically improved as the exposure of the protons to the EM pulse’s electric field is prolonged by extending the length of the coil.
2 Experiment
The experiment was performed using the TARANIS laser[Reference Dzelzainis, Nersisyan, Riley, Romagnani, Ahmed, Bigongiari, Borghesi, Doria, Dromey, Makita, White, Kar, Marlow, Ramakrisha, Sarri, Zakaul-islam, Zepf and Lewis20] at Queen’s university Belfast, employing the chirped pulse amplification (CPA) pulse of duration
![]() ${\sim}700~\text{fs}$
and energy
${\sim}700~\text{fs}$
and energy
![]() ${\sim}4~\text{J}$
on the target. The laser pulse was focused by an
${\sim}4~\text{J}$
on the target. The laser pulse was focused by an
![]() $f/3$
off axis parabola on an Au foils of thickness
$f/3$
off axis parabola on an Au foils of thickness
![]() ${\sim}10~\unicode[STIX]{x03BC}\text{m}$
, delivering peak intensity
${\sim}10~\unicode[STIX]{x03BC}\text{m}$
, delivering peak intensity
![]() ${\sim}2\times 10^{19}~\text{W}~\text{cm}^{-2}$
. The intensity contrast of the laser at 1–2 ns before the main pulse (due to amplified spontaneous emission (ASE)) was
${\sim}2\times 10^{19}~\text{W}~\text{cm}^{-2}$
. The intensity contrast of the laser at 1–2 ns before the main pulse (due to amplified spontaneous emission (ASE)) was
![]() ${\sim}10^{7}$
. Stacks of multilayer radiochromic films (RCFs), placed at 23 mm from the interaction foil, were employed to obtain energy resolved footprints of the proton beam. The RCF dose response was cross-calibrated using RCFs exposed to different known proton doses from a conventional accelerator[Reference Kirby, Green, Fiorini, Parker, Romagnani, Doria, Kar, Lewis, Borghesi and Palmans21]. A schematics of the experimental setup used for transverse probing of the coil is shown in Figure 1(a). The wire connecting the target foil to the ground was turned into a helical coil of 9 windings [as shown in Figure 1(b)], and was placed within the field of view of the proton probe. The helical coil was made of Aluminium wire of
${\sim}10^{7}$
. Stacks of multilayer radiochromic films (RCFs), placed at 23 mm from the interaction foil, were employed to obtain energy resolved footprints of the proton beam. The RCF dose response was cross-calibrated using RCFs exposed to different known proton doses from a conventional accelerator[Reference Kirby, Green, Fiorini, Parker, Romagnani, Doria, Kar, Lewis, Borghesi and Palmans21]. A schematics of the experimental setup used for transverse probing of the coil is shown in Figure 1(a). The wire connecting the target foil to the ground was turned into a helical coil of 9 windings [as shown in Figure 1(b)], and was placed within the field of view of the proton probe. The helical coil was made of Aluminium wire of
![]() $60~\unicode[STIX]{x03BC}\text{m}$
diameter. The radius of the helical coil was
$60~\unicode[STIX]{x03BC}\text{m}$
diameter. The radius of the helical coil was
![]() ${\sim}450~\unicode[STIX]{x03BC}\text{m}$
and the average pitch of the coil was
${\sim}450~\unicode[STIX]{x03BC}\text{m}$
and the average pitch of the coil was
![]() ${\sim}330~\unicode[STIX]{x03BC}\text{m}$
, which varied over the coil length due to imperfections in the target fabrication. However, the precise location and shape of each winding was measured from target images taken before the shot. The distance between the interaction foil and the mid plane of the helical coil was
${\sim}330~\unicode[STIX]{x03BC}\text{m}$
, which varied over the coil length due to imperfections in the target fabrication. However, the precise location and shape of each winding was measured from target images taken before the shot. The distance between the interaction foil and the mid plane of the helical coil was
![]() ${\sim}3~\text{mm}$
. In this case, a coil of similar dimensions was connected to the rear side of the laser irradiated foil, with the coil axis normal to the foil and the other side of the coil connected to ground.
${\sim}3~\text{mm}$
. In this case, a coil of similar dimensions was connected to the rear side of the laser irradiated foil, with the coil axis normal to the foil and the other side of the coil connected to ground.
3 Results and discussion
3.1 Transverse probing
Figures 1(c) and (d) show the proton images obtained by 5.5 and 3 MeV protons, respectively, illustrating the flow of the EM pulse towards the ground (bottom of the images) through the helical coil. As can be seen in the radiograph shown in Figure 1(c), a strong deflection of the probe protons is apparent at the middle of the coil (winding F3). At a later probing time, as shown in Figure 1(d), the strongest deflection of the probe protons appears in the lower section of the helical coil (winding F4–F5), while the width of the top three windings (F1–F3) matches with their geometrical shadows, which suggests the absence of a significant electric field around these windings.
By following the EM pulse through each winding of the helical coil at different probing times, as shown in the different RCF layers of the stack, the temporal profile of the travelling EM pulse can be reconstructed. In comparison to the square wave pattern used for the EM pulse characterization in the Refs. [Reference Kar, Ahmed, Prasad, Cerchez, Brauckmann, Aurand, Cantono, Hadjisolomou, Lewis, Macchi, Nersisyan, Robinson, Schroer, Swantusch, Zepf, Willi and Borghesi16, Reference Ahmed, Kar, Cantono, Nersisyan, Brauckmann, Doria, Gwynne, Macchi, Naughton, Willi, Lewis and Borghesi17], the helical coil geometry slightly complicates the data analysis as the different points on a given winding will be probed at different times even by protons of a fixed energy.

Figure 2. (a) and (b) show the schematics (side and top view, respectively) of the arrangement for transverse probing of the helical winding. F and B represent, respectively, the front and back principal probing points on a winding chosen for analysis. The difference in probing times for the two principal points arises due to the different proton time of flights. (c) shows the temporal profile of the pulse travelling along the wire of the helical coil as obtained from the data shown in Figure 1.

Figure 3. (a) Image of the target used for longitudinal probing. The coil had
![]() ${\sim}900~\unicode[STIX]{x03BC}\text{m}$
diameter and 1.9 mm long and consisted of 8 windings with average pitch of
${\sim}900~\unicode[STIX]{x03BC}\text{m}$
diameter and 1.9 mm long and consisted of 8 windings with average pitch of
![]() ${\sim}260~\unicode[STIX]{x03BC}\text{m}$
. (b), (c) and (d) show experimental, spatially resolved dose profiles of the proton beam for energies 3.0, 4.4 and 5.5 MeV, respectively. (e) shows the percentage reduction of diameter of the central part of the beam with respect to proton energies (MeV), as obtained from the experimental (black) and simulated (red) RCF images.
${\sim}260~\unicode[STIX]{x03BC}\text{m}$
. (b), (c) and (d) show experimental, spatially resolved dose profiles of the proton beam for energies 3.0, 4.4 and 5.5 MeV, respectively. (e) shows the percentage reduction of diameter of the central part of the beam with respect to proton energies (MeV), as obtained from the experimental (black) and simulated (red) RCF images.
The probing time at a given point,
![]() $P(x,y,z)$
, on the helical coil can be obtained as
$P(x,y,z)$
, on the helical coil can be obtained as
![]() $t_{\text{proton}}(E_{p},x,y,z)=\sqrt{x^{2}+y^{2}+z^{2}}/\sqrt{2E_{p}/m_{p}}$
, where
$t_{\text{proton}}(E_{p},x,y,z)=\sqrt{x^{2}+y^{2}+z^{2}}/\sqrt{2E_{p}/m_{p}}$
, where
![]() $E_{p}$
is the energy of the probe protons,
$E_{p}$
is the energy of the probe protons,
![]() $m_{p}$
is the proton mass and the coordinate system is centered on the proton source location. For simplicity, two principal points in each winding were considered in our analysis, in our analysis, i.e. the front (F) and back (B) principal points shown in Figure 2(a), and the principal points where deflections overlap were discarded in the analysis. The difference in time at which these two points are probed by protons of a given energy arises due to their different distances from the proton source. For example, the probing time for 3 MeV protons [corresponding to the RCF image shown in Figure 1(d)] at the two principal points (F and B) on the F4 winding were
$m_{p}$
is the proton mass and the coordinate system is centered on the proton source location. For simplicity, two principal points in each winding were considered in our analysis, in our analysis, i.e. the front (F) and back (B) principal points shown in Figure 2(a), and the principal points where deflections overlap were discarded in the analysis. The difference in time at which these two points are probed by protons of a given energy arises due to their different distances from the proton source. For example, the probing time for 3 MeV protons [corresponding to the RCF image shown in Figure 1(d)] at the two principal points (F and B) on the F4 winding were
![]() ${\sim}104$
and
${\sim}104$
and
![]() ${\sim}143~\text{ps}$
, respectively.
${\sim}143~\text{ps}$
, respectively.
After measuring the proton deflection in the data for a number of principal points along the helical coil, a linear charge density associated to the pulse was estimated at the corresponding probing time (
![]() $t_{\text{proton}}$
) by matching the experimental proton deflection with the deflection produced by the particle tracing (PTRACE) simulations[Reference Schiavi22], as discussed in Refs. [Reference Kar, Ahmed, Prasad, Cerchez, Brauckmann, Aurand, Cantono, Hadjisolomou, Lewis, Macchi, Nersisyan, Robinson, Schroer, Swantusch, Zepf, Willi and Borghesi16, Reference Ahmed, Kar, Cantono, Nersisyan, Brauckmann, Doria, Gwynne, Macchi, Naughton, Willi, Lewis and Borghesi17]. The length of the wire (
$t_{\text{proton}}$
) by matching the experimental proton deflection with the deflection produced by the particle tracing (PTRACE) simulations[Reference Schiavi22], as discussed in Refs. [Reference Kar, Ahmed, Prasad, Cerchez, Brauckmann, Aurand, Cantono, Hadjisolomou, Lewis, Macchi, Nersisyan, Robinson, Schroer, Swantusch, Zepf, Willi and Borghesi16, Reference Ahmed, Kar, Cantono, Nersisyan, Brauckmann, Doria, Gwynne, Macchi, Naughton, Willi, Lewis and Borghesi17]. The length of the wire (
![]() $l_{\text{delay}}$
) from the laser interaction point to the given point was measured from the target images taken before the shots. Assuming the velocity of the EM pulse along a wire to be
$l_{\text{delay}}$
) from the laser interaction point to the given point was measured from the target images taken before the shots. Assuming the velocity of the EM pulse along a wire to be
![]() $0.96c$
(where
$0.96c$
(where
![]() $c$
is the speed of light in vacuum), as estimated from the previous measurements reported in Refs. [Reference Kar, Ahmed, Prasad, Cerchez, Brauckmann, Aurand, Cantono, Hadjisolomou, Lewis, Macchi, Nersisyan, Robinson, Schroer, Swantusch, Zepf, Willi and Borghesi16, Reference Ahmed, Kar, Cantono, Nersisyan, Brauckmann, Doria, Gwynne, Macchi, Naughton, Willi, Lewis and Borghesi17], the arrival time of the pulse at the point under consideration was calculated as
$c$
is the speed of light in vacuum), as estimated from the previous measurements reported in Refs. [Reference Kar, Ahmed, Prasad, Cerchez, Brauckmann, Aurand, Cantono, Hadjisolomou, Lewis, Macchi, Nersisyan, Robinson, Schroer, Swantusch, Zepf, Willi and Borghesi16, Reference Ahmed, Kar, Cantono, Nersisyan, Brauckmann, Doria, Gwynne, Macchi, Naughton, Willi, Lewis and Borghesi17], the arrival time of the pulse at the point under consideration was calculated as
![]() $t_{\text{charge}}=l_{\text{delay}}/0.96c$
. By repeating the analysis for each principal points across the coil, the temporal profile of the pulse was reconstructed, which is shown in Figure 2(c). As can be seen, the temporal profile displaying
$t_{\text{charge}}=l_{\text{delay}}/0.96c$
. By repeating the analysis for each principal points across the coil, the temporal profile of the pulse was reconstructed, which is shown in Figure 2(c). As can be seen, the temporal profile displaying
![]() ${\sim}5~\text{ps}$
rise and
${\sim}5~\text{ps}$
rise and
![]() ${\sim}12~\text{ps}$
decay is in a broad agreement with previous measurements taken under similar experimental laser conditions[Reference Ahmed, Kar, Cantono, Nersisyan, Brauckmann, Doria, Gwynne, Macchi, Naughton, Willi, Lewis and Borghesi17, Reference Kar, Ahmed, Nersisyan, Brauckmann, Hanton, Giesecke, Naughton, Willi, Lewis and Borghesi18].
${\sim}12~\text{ps}$
decay is in a broad agreement with previous measurements taken under similar experimental laser conditions[Reference Ahmed, Kar, Cantono, Nersisyan, Brauckmann, Doria, Gwynne, Macchi, Naughton, Willi, Lewis and Borghesi17, Reference Kar, Ahmed, Nersisyan, Brauckmann, Hanton, Giesecke, Naughton, Willi, Lewis and Borghesi18].

Figure 4. (a) shows a schematic of the setup used for the shot taken with a 3.3 mm long helical coil with RCF placed at 70 mm from the interaction foil. (b), (c) and (d) show the raw RCF images for 3.0, 6.6 and 9.6 MeV protons respectively, where the pronounced focusing of the channelled beam of 3 MeV protons can be seen in (b), in contrast to the geometrical projection of the exit winding of the coil at the RCF plane shown by the red dashed circle.
3.2 Longitudinal probing
In order to control the inherent shortcomings of the TNSA-driven proton beams, viz. large divergence and broad energy spectrum, a guiding geometry exploiting the high electric field of the travelling EM pulse was envisioned by Kar et al. [Reference Kar, Ahmed, Prasad, Cerchez, Brauckmann, Aurand, Cantono, Hadjisolomou, Lewis, Macchi, Nersisyan, Robinson, Schroer, Swantusch, Zepf, Willi and Borghesi16]. The scheme was based on attaching a helical coil longitudinally to the rear surface of the interaction foil, with the coil axis normal to the foil, so that the TNSA protons can propagate through it. In this arrangement, the helical coil provides a sole path for the flow of the pulse around the proton beam axis. By suitably choosing radius and pitch of coil, it is possible to synchronize the longitudinal propagation of the EM pulse with transiting protons of a given energy, over an extended propagation length. The radial and longitudinal components of the electric field of the pulse act, respectively, towards focusing and acceleration of the protons synchronous with the pulse. On the other hand, the unsynchronized protons will maintain their intrinsic divergence, which will enable spectral tailoring of the beam at the coil output, e.g. by using a spatial aperture at a far distance from the target.
In order to understand more in detail the effect of the electric field on a beam of protons while transiting through a coil, longitudinal probing was carried out by employing a short coil of 1.9 mm long and radius of
![]() ${\sim}450~\unicode[STIX]{x03BC}\text{m}$
. Figures 3(b)–(d) show the spatially resolved dose profiles of 3.0, 4.4 and 5.5 MeV protons, respectively obtained from the shot. As can be seen, the proton beam profiles show two pronounced features, central part of the beam and circular ring patterns around it. These ring patterns are produced by protons escaping through the side of the coil, while also being deflected by the electric field around the coiled wire. On the other hand, the central part of the proton beam is channelled through the helical coil. If the protons are travelling in synchronization with the pulse moving along the helical path, which is broadly the case for 3.0–4.4 MeV protons, the radial electric field within the helical coil will deflect the protons towards the axis of the coil. Whereas, the 5.5 MeV protons are not affected by the radial electric field, as they are traveling ahead of the electric field region inside the coil. This energy dependent behaviour can be clearly seen in Figures 3(b)–(d), as the diameter of the central part varies significantly with proton energy.
${\sim}450~\unicode[STIX]{x03BC}\text{m}$
. Figures 3(b)–(d) show the spatially resolved dose profiles of 3.0, 4.4 and 5.5 MeV protons, respectively obtained from the shot. As can be seen, the proton beam profiles show two pronounced features, central part of the beam and circular ring patterns around it. These ring patterns are produced by protons escaping through the side of the coil, while also being deflected by the electric field around the coiled wire. On the other hand, the central part of the proton beam is channelled through the helical coil. If the protons are travelling in synchronization with the pulse moving along the helical path, which is broadly the case for 3.0–4.4 MeV protons, the radial electric field within the helical coil will deflect the protons towards the axis of the coil. Whereas, the 5.5 MeV protons are not affected by the radial electric field, as they are traveling ahead of the electric field region inside the coil. This energy dependent behaviour can be clearly seen in Figures 3(b)–(d), as the diameter of the central part varies significantly with proton energy.
By considering the projection of the exit ring of the coil over the RCF plane, the reduction in diameter of the central part was estimated, which is very pronounced for low energy protons, as illustrated in Figure 3(e). For instance, the diameter for 3.0 MeV protons was
![]() ${\sim}6~\text{mm}$
at the RCF plane, which corresponds to a
${\sim}6~\text{mm}$
at the RCF plane, which corresponds to a
![]() ${\sim}25\%$
reduction in beam divergence. A series of 3D particle tracing simulation were performed using the pulse temporal profile shown in Figure 2(c). The peak of the temporal profile was varied until an agreement with the experimental results was achieved. The best match, as shown in Figure 3(e), was obtained for a peak value of
${\sim}25\%$
reduction in beam divergence. A series of 3D particle tracing simulation were performed using the pulse temporal profile shown in Figure 2(c). The peak of the temporal profile was varied until an agreement with the experimental results was achieved. The best match, as shown in Figure 3(e), was obtained for a peak value of
![]() $7.5~\unicode[STIX]{x03BC}\text{C}~\text{m}^{-1}$
, which is within our experimental error and possible shot-to-shot fluctuations.
$7.5~\unicode[STIX]{x03BC}\text{C}~\text{m}^{-1}$
, which is within our experimental error and possible shot-to-shot fluctuations.
Although only a moderate reduction in beam divergence was obtained in this case (as compared for example to Ref. [Reference Kar, Ahmed, Prasad, Cerchez, Brauckmann, Aurand, Cantono, Hadjisolomou, Lewis, Macchi, Nersisyan, Robinson, Schroer, Swantusch, Zepf, Willi and Borghesi16]), the observed energy dependance and its agreement with simulations underpin the underlying mechanism of the technique. One of the promising features of the helical coil lens is the transient nature of the travelling focusing field, which provides a flexibility to control the beam divergence of a given range of proton energies by carefully choosing the dimensions of the helical coil. Moreover, by increasing the length of the helical coil, while keeping the synchronization with the same slice of the energy spectrum, the focusing field can be applied for a longer time, which would result in a further reduction in the diameter of the channelled beam. In order to demonstrate this effect, a helical coil target of similar diameter and pitch (synchronizing around 3–4 MeV protons) as shown in Figure 4, but of length
![]() ${\sim}3.3~\text{mm}$
was deployed. In this case the RCF stack was placed at the significantly larger distance of
${\sim}3.3~\text{mm}$
was deployed. In this case the RCF stack was placed at the significantly larger distance of
![]() ${\sim}70~\text{mm}$
from the target in order to measure the beam divergence with higher accuracy. The raw RCF data obtained from the shot is shown in Figures 4(b)–(d), corresponding to spatial profiles of (3.0, 6.5 and 9.6)
${\sim}70~\text{mm}$
from the target in order to measure the beam divergence with higher accuracy. The raw RCF data obtained from the shot is shown in Figures 4(b)–(d), corresponding to spatial profiles of (3.0, 6.5 and 9.6)
![]() $\pm$
0.5 MeV protons, respectively. As can be seen, the beam diameter of the 3.0 MeV protons at the detector plane was
$\pm$
0.5 MeV protons, respectively. As can be seen, the beam diameter of the 3.0 MeV protons at the detector plane was
![]() ${\sim}1~\text{mm}$
, which corresponds to a beam divergence of less than
${\sim}1~\text{mm}$
, which corresponds to a beam divergence of less than
![]() $1^{\circ }$
. Furthermore, strong focusing of the proton beam also resulted in a commensurate enhancement of the proton flux within the focused region. Such high flux, pencil beam of protons would be of interest for many application, including, for instance, the creation of warm dense matter by isochoric heating[Reference Patel, Mackinnon, Key, Cowan, Foord, Allen, Price, Ruhl, Springer and Stephens8].
$1^{\circ }$
. Furthermore, strong focusing of the proton beam also resulted in a commensurate enhancement of the proton flux within the focused region. Such high flux, pencil beam of protons would be of interest for many application, including, for instance, the creation of warm dense matter by isochoric heating[Reference Patel, Mackinnon, Key, Cowan, Foord, Allen, Price, Ruhl, Springer and Stephens8].
4 Conclusions
The propagation of EM pulses in a helical coil, and their application towards improving the beam parameters of laser-driven ions were discussed. The temporal profile of an EM pulse travelling along a helical coil was characterized by transverse proton probing of the coil, which is in agreement with the previously reported measurements while probing the pulse-carrying wire in a planner geometry. By directing the transient EM pulses in a helical path around the proton beams, the angular and spectral properties of the proton beams can be controlled. The effect of the radial electric field inside a pulse-carrying coil towards focusing of the transiting protons was studied by probing a short coil longitudinally. Extending the coil length resulted in a highly collimated proton beam of less than
![]() $1^{\circ }$
beam divergence. This technique may provide a platform for producing collimated beams for many potential applications, such as the creation of warm dense matter, radiobiology and radiotherapy.
$1^{\circ }$
beam divergence. This technique may provide a platform for producing collimated beams for many potential applications, such as the creation of warm dense matter, radiobiology and radiotherapy.
Acknowledgements
The authors acknowledge funding from EPSRC, [EP/J002550/1-Career Acceleration Fellowship held by S. K., EP/L002221/1, EP/K022415/1, and EP/I029206/1], SBF-TR18 and GRK1203, EC-GA284464 and Invest Northern Ireland (POC-329). Authors acknowledge A. Schiavi (Univ. Roma 1, Italy) for the use of the particle tracing code, PTRACE. Data associated with research published in this paper can be accessible at http://dx.doi.org/10.17034/7ae254da-f94b-4c85-a07b-02efba38030a.