1 Introduction
High power lasers can create extreme conditions in the laboratory relevant to astrophysical systems[Reference Remington, Drake and Ryutov1–Reference Cross, Reville and Gregori3]. With the scaling law[Reference Ryutov, Drake, Kane, Liang, Remington and Wood-Vasey4], it presents a new route, laboratory astrophysics, to investigate the astrophysical scenarios, such as shock generation in supernova explosions[Reference Hester5], magnetic reconnection occurring at solar flares[Reference Yamada, Kulsrud and Ji6, Reference Yamada, Yoo and Myers7], and Herbig–Haro objects associated with young stellar object formation[Reference Reipurth and Bally8].
One of the hottest research fields is astrophysical shocks, which are ubiquitous and observed in a wide range of astrophysical environments, such as solar-terrestrial space, supernova explosions and gamma-ray bursts. Figure 1(a) shows a typical composite image of the supernova remnant 1006 (SNR 1006) caused by the destruction of a white dwarf star, which is located about 7000 light years from the Earth[Reference Aya, Ryo, Masaru and Katsuji9]. A sharp edge appears in the interaction region where the exploded matters with high velocity penetrate through the rare interstellar mediums (ISMs), indicating that a shock is formed. The shock transition region is measured about 0.04 pc (
![]() $=1.2\times 10^{17}~\text{cm}$
),
$=1.2\times 10^{17}~\text{cm}$
),
![]() $1/400$
of the mean free path (MFP
$1/400$
of the mean free path (MFP
![]() ${\sim}$
13 pc)[Reference Takabe, Kato, Sakawa, Kuramitsu, Morita, Kadono, Shigemori, Otani, Nagatomo, Norimatsu, Dono, Endo, Miyanishi, Kimura, Shiroshita, Ozaki, Kodama, Fujioka, Nishimura, Salzman, Loupias, Gregory, Koenig, Waugh, Woolsey, Kato, Li, Dong, Wang, Zhang, Zhao, Wang, Wei, Shi, Zhao, Zhang, Wen, Zhang, Hu, Liu, Ding, Zhang, Tang, Zhang, Zheng, Sheng and Zhang10]. Obviously, it is collisionless and mediated by the collective effect, instead of the Coulomb collisions. This shock has attracted much interest in its formation mechanism, generation/amplification of the magnetic fields[Reference Medvedev and Loeb11, Reference Chang, Apitkovsky and Arons12], and the spray of the energetic cosmic rays[Reference Aharonian, Akhperjanian, Aye, Bazer-Bachi, Beilicke, Benbow, Berge, Berghaus, Bernlohr, Bolz, Boisson, Borgmeier, Breitling, Brown, Bussons Gordo, Chadwick, Chitnis, Chounet, Cornils, Costamante, Degrange, Djannati-Ata, Drury, Ergin, Espigat, Feinstein, Fleury, Fontaine, Funk, Gallant, Giebels, Gillessen, Goret, Guy, Hadjichristidis, Hauser, Heinzelmann, Henri, Hermann, Hinton, Hofmann, Holleran, Horns, de Jager, Jung, Khélifi, Komin, Konopelko, Latham, Le Gallou, Lemoine, Lemiere, Leroy, Lohse, Marcowith, Masterson, McComb, de Naurois, Nolan, Noutsos, Orford, Osborne, Ouchrif, Panter, Pelletier, Pita, Pohl, Puhlhofer, Punch, Raubenheimer, Raue, Raux, Rayner, Redondo, Reimer, Reimer, Ripken, Rivoal, Rob, Rolland, Rowell, Sahakian, Sauge, Schlenker, Schlickeiser, Schuster, Schwanke, Siewert, Sol, Steenkamp, Stegmann, Tavernet, Théoret, Tluczykont, van der Walt, Vasileiadis, Vincent, Visser, Volk and Wagner13–Reference Spitkovsky15].
${\sim}$
13 pc)[Reference Takabe, Kato, Sakawa, Kuramitsu, Morita, Kadono, Shigemori, Otani, Nagatomo, Norimatsu, Dono, Endo, Miyanishi, Kimura, Shiroshita, Ozaki, Kodama, Fujioka, Nishimura, Salzman, Loupias, Gregory, Koenig, Waugh, Woolsey, Kato, Li, Dong, Wang, Zhang, Zhao, Wang, Wei, Shi, Zhao, Zhang, Wen, Zhang, Hu, Liu, Ding, Zhang, Tang, Zhang, Zheng, Sheng and Zhang10]. Obviously, it is collisionless and mediated by the collective effect, instead of the Coulomb collisions. This shock has attracted much interest in its formation mechanism, generation/amplification of the magnetic fields[Reference Medvedev and Loeb11, Reference Chang, Apitkovsky and Arons12], and the spray of the energetic cosmic rays[Reference Aharonian, Akhperjanian, Aye, Bazer-Bachi, Beilicke, Benbow, Berge, Berghaus, Bernlohr, Bolz, Boisson, Borgmeier, Breitling, Brown, Bussons Gordo, Chadwick, Chitnis, Chounet, Cornils, Costamante, Degrange, Djannati-Ata, Drury, Ergin, Espigat, Feinstein, Fleury, Fontaine, Funk, Gallant, Giebels, Gillessen, Goret, Guy, Hadjichristidis, Hauser, Heinzelmann, Henri, Hermann, Hinton, Hofmann, Holleran, Horns, de Jager, Jung, Khélifi, Komin, Konopelko, Latham, Le Gallou, Lemoine, Lemiere, Leroy, Lohse, Marcowith, Masterson, McComb, de Naurois, Nolan, Noutsos, Orford, Osborne, Ouchrif, Panter, Pelletier, Pita, Pohl, Puhlhofer, Punch, Raubenheimer, Raue, Raux, Rayner, Redondo, Reimer, Reimer, Ripken, Rivoal, Rob, Rolland, Rowell, Sahakian, Sauge, Schlenker, Schlickeiser, Schuster, Schwanke, Siewert, Sol, Steenkamp, Stegmann, Tavernet, Théoret, Tluczykont, van der Walt, Vasileiadis, Vincent, Visser, Volk and Wagner13–Reference Spitkovsky15].
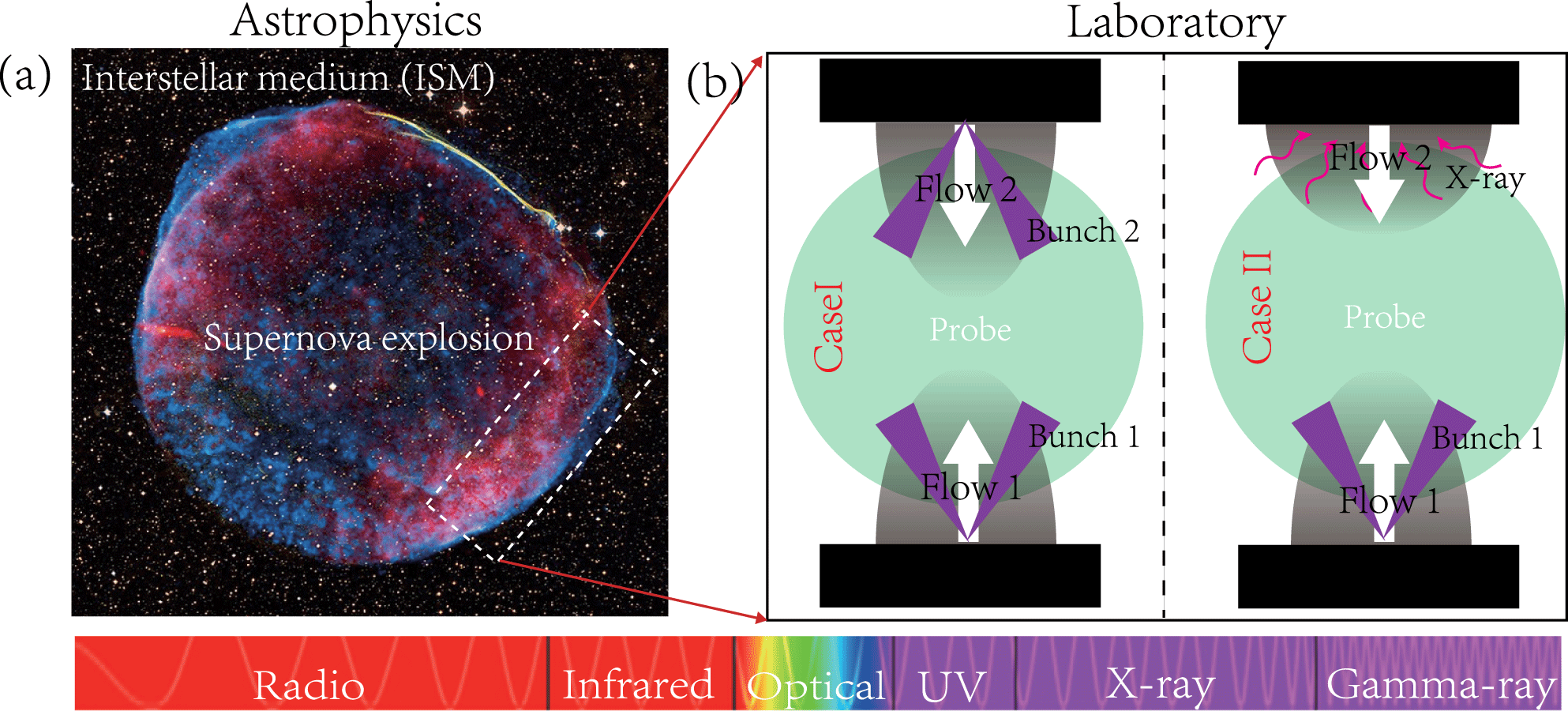
Figure 1. (a) A composite image of collisionless shock formed in the SNRs[18]. Color stands for the observation wavelength, as shown in the color bar. (b) The experimental configurations to simulate the astrophysical CPFs. Here, two schemes are used to generate counter-streaming flows. Case I is a symmetrical one, where both flows are directly ablating both facing surfaces of the foils. Case II is an unsymmetrical one, where only one foil is ablating by one bunch and the other side foil is heated by the X-ray from laser–target interaction. The probe beam (outwards) transversely passes through the interaction region for optical diagnostics.
Figure 1(b) shows a schematic drawing of the counter-streaming plasma flows (CPFs) in laboratory, which are designed to study the shock. Both flows are generated from the opposing target foils. Two schemes (Cases I and II) are used to generate CPFs: (Case I) one is using two laser bunches directly ablating the facing surfaces of the foils; and (Case II) the other one is only using one laser bunch ablating a foil to blow out an incoming flow, the reverse flow is generated due to photoionization of the other foil by the intense X-ray from the laser-irradiation target.
No matter which scheme is applied, it must achieve the collisionless conditions between CPFs, i.e., the MFP larger than the interaction scale,
![]() $L$
(target separation or shock transition width, in our experiment
$L$
(target separation or shock transition width, in our experiment
![]() $L=4.5~\text{mm}$
). The simplified expression of MFP can be written in Gaussian units as[Reference Chenais-Popovics, Renaudin, Rancu, Gilleron, Gauthier, Larroche, Peyrusse, Dirksmoller, Sondhauss, Missalla, Uschmann, Forster, Renner and Krousky16]
$L=4.5~\text{mm}$
). The simplified expression of MFP can be written in Gaussian units as[Reference Chenais-Popovics, Renaudin, Rancu, Gilleron, Gauthier, Larroche, Peyrusse, Dirksmoller, Sondhauss, Missalla, Uschmann, Forster, Renner and Krousky16]
![]() $\unicode[STIX]{x1D706}_{mfp}=m_{i}^{2}\unicode[STIX]{x1D710}_{12}^{4}/(4\unicode[STIX]{x1D70B}e^{4}Z^{4}n_{i}\ln \unicode[STIX]{x1D6EC}_{12})$
, where
$\unicode[STIX]{x1D706}_{mfp}=m_{i}^{2}\unicode[STIX]{x1D710}_{12}^{4}/(4\unicode[STIX]{x1D70B}e^{4}Z^{4}n_{i}\ln \unicode[STIX]{x1D6EC}_{12})$
, where
![]() $m_{i}$
is the ion mass,
$m_{i}$
is the ion mass,
![]() $\unicode[STIX]{x1D710}_{12}=2\unicode[STIX]{x1D710}$
is the relative velocity of each flow,
$\unicode[STIX]{x1D710}_{12}=2\unicode[STIX]{x1D710}$
is the relative velocity of each flow,
![]() $e$
is the electric charge,
$e$
is the electric charge,
![]() $Z$
is the average charge state,
$Z$
is the average charge state,
![]() $n_{e}=Zn_{i}$
is the electron density and
$n_{e}=Zn_{i}$
is the electron density and
![]() $\ln \unicode[STIX]{x1D6EC}$
is the Coulomb logarithm. We can see that the desirable collisionless conditions in the laboratory are higher flow velocity and lower-
$\ln \unicode[STIX]{x1D6EC}$
is the Coulomb logarithm. We can see that the desirable collisionless conditions in the laboratory are higher flow velocity and lower-
![]() $Z$
target material. We can increase the driven laser energy,
$Z$
target material. We can increase the driven laser energy,
![]() $E_{L}$
, or optimize the laser absorption coefficient,
$E_{L}$
, or optimize the laser absorption coefficient,
![]() $f$
, to increase the flow velocity, which mainly depends on the absorbed driven laser energy (
$f$
, to increase the flow velocity, which mainly depends on the absorbed driven laser energy (
![]() $1/2n_{i}m_{i}\unicode[STIX]{x1D710}^{2}\times V=E_{k}=fE_{L}$
, where
$1/2n_{i}m_{i}\unicode[STIX]{x1D710}^{2}\times V=E_{k}=fE_{L}$
, where
![]() $n_{i}$
is the ion number density and
$n_{i}$
is the ion number density and
![]() $V$
is the plasma volume)[Reference Ciardi, Vinci, Fuchs, Albertazzi, Riconda, Pépin and Portugall17]. The lower-
$V$
is the plasma volume)[Reference Ciardi, Vinci, Fuchs, Albertazzi, Riconda, Pépin and Portugall17]. The lower-
![]() $Z$
material of the solid target can be chosen as CH, CD, DLi, etc.
$Z$
material of the solid target can be chosen as CH, CD, DLi, etc.
Here we will review the achievements of the collisionless shock at SG-II laser facility[Reference Zhong, Lin, Li, Wang, Li, Zhang, Yuan, Ping, Wei, Wang, Su, Li, Han, Liao, Yin, Fang, Yuan, Wang, Sun, Liang, Wang, Ding, He, Zhu, Sheng, Li, Zhao and Zhang19–Reference Yuan and Li21], which can deliver a total energy of 2.0 kJ in 1 ns at
![]() $3\unicode[STIX]{x1D714}$
(351 nm). Eight SG-II laser beams are divided into two bunches, each bunch consisting of four beams. The overlapped focal spot is
$3\unicode[STIX]{x1D714}$
(351 nm). Eight SG-II laser beams are divided into two bunches, each bunch consisting of four beams. The overlapped focal spot is
![]() $150{-}200~\unicode[STIX]{x03BC}\text{m}$
, giving an intensity of
$150{-}200~\unicode[STIX]{x03BC}\text{m}$
, giving an intensity of
![]() ${\sim}10^{15}~\text{W}\cdot \text{cm}^{-2}$
. The main diagnostics is using optical probe, including Nomarski interferometer and shadowgraphy. As shown in Figure 1(b), a probe beam with a wavelength of
${\sim}10^{15}~\text{W}\cdot \text{cm}^{-2}$
. The main diagnostics is using optical probe, including Nomarski interferometer and shadowgraphy. As shown in Figure 1(b), a probe beam with a wavelength of
![]() $2\unicode[STIX]{x1D714}$
(527 nm) and duration of 30 ps transversely passes through the interaction region, measuring the density, flow velocity and so on. In this paper, the evolution of the electrostatic shock (ES) and filamentation instability is successfully observed by optimizing experimental conditions in CPFs. Inspired by the configuration of the CPFs, we also perform an exploratory experiment relevant to neutron astrophysics to distinguish between collisionless and collisional effects in CPFs.
$2\unicode[STIX]{x1D714}$
(527 nm) and duration of 30 ps transversely passes through the interaction region, measuring the density, flow velocity and so on. In this paper, the evolution of the electrostatic shock (ES) and filamentation instability is successfully observed by optimizing experimental conditions in CPFs. Inspired by the configuration of the CPFs, we also perform an exploratory experiment relevant to neutron astrophysics to distinguish between collisionless and collisional effects in CPFs.
2 Experimental results
2.1 The evolution of the symmetrical CPFs
The left panel in Figure 2 shows the typical interferograms of the evolution of the CPFs, which are produced by two laser-bunches ablating CH foils[Reference Yuan, Li, Liu, Zhang, Zhong, Zheng, Dong, Chen, Sakawa, Morita, Kuramitsu, Kato, Takabe, Rhee, Zhu, Zhao and Zhang22–Reference Yuan, Li, Su, Liao, Yin, Zhu and Zhang24]. The right panel shows the corresponding density profile obtained by the Abel inversion. Before shock formation (
![]() $t<2~\text{ns}$
), we measure the free expansion of the plasma flow with electron density of
$t<2~\text{ns}$
), we measure the free expansion of the plasma flow with electron density of
![]() $10^{19}~\text{cm}^{-3}$
and flow velocity of
$10^{19}~\text{cm}^{-3}$
and flow velocity of
![]() $1000~\text{km}\cdot \text{s}^{-1}$
. During shock formation (
$1000~\text{km}\cdot \text{s}^{-1}$
. During shock formation (
![]() $t\sim 2~\text{ns}$
), both flows interact with each other and result in the sudden fringes shift at the midplane, indicating that a large-density jump (
$t\sim 2~\text{ns}$
), both flows interact with each other and result in the sudden fringes shift at the midplane, indicating that a large-density jump (
![]() $n_{\text{shock}}/n_{\text{flow}}\sim 3$
) is generated. After that (
$n_{\text{shock}}/n_{\text{flow}}\sim 3$
) is generated. After that (
![]() $t>3~\text{ns}$
), the shifted fringes become smooth and filament structures parallel to the flow direction appear in the central region, indicating that the excited shock is perhaps dissipated by the growing filamentary structures (
$t>3~\text{ns}$
), the shifted fringes become smooth and filament structures parallel to the flow direction appear in the central region, indicating that the excited shock is perhaps dissipated by the growing filamentary structures (
![]() $t>5~\text{ns}$
). Since the MFP (
$t>5~\text{ns}$
). Since the MFP (
![]() $\unicode[STIX]{x1D706}_{ii}$
) scales as
$\unicode[STIX]{x1D706}_{ii}$
) scales as
![]() $1/Z^{4}$
, the
$1/Z^{4}$
, the
![]() $\unicode[STIX]{x1D706}_{ii}$
for hydrogen ions (
$\unicode[STIX]{x1D706}_{ii}$
for hydrogen ions (
![]() $Z=1$
) will be higher than that for carbon ions (
$Z=1$
) will be higher than that for carbon ions (
![]() $Z=6$
). Here we just use
$Z=6$
). Here we just use
![]() $Z=6$
to calculate the lower limit of MFP, whose value is estimated as 180 mm, indicating that ions from inter-flows can freely interpenetrate each other. Consequently, these observed features in the CPFs should be induced by plasma collective behaviors, instead of the hydrodynamic stagnation.
$Z=6$
to calculate the lower limit of MFP, whose value is estimated as 180 mm, indicating that ions from inter-flows can freely interpenetrate each other. Consequently, these observed features in the CPFs should be induced by plasma collective behaviors, instead of the hydrodynamic stagnation.
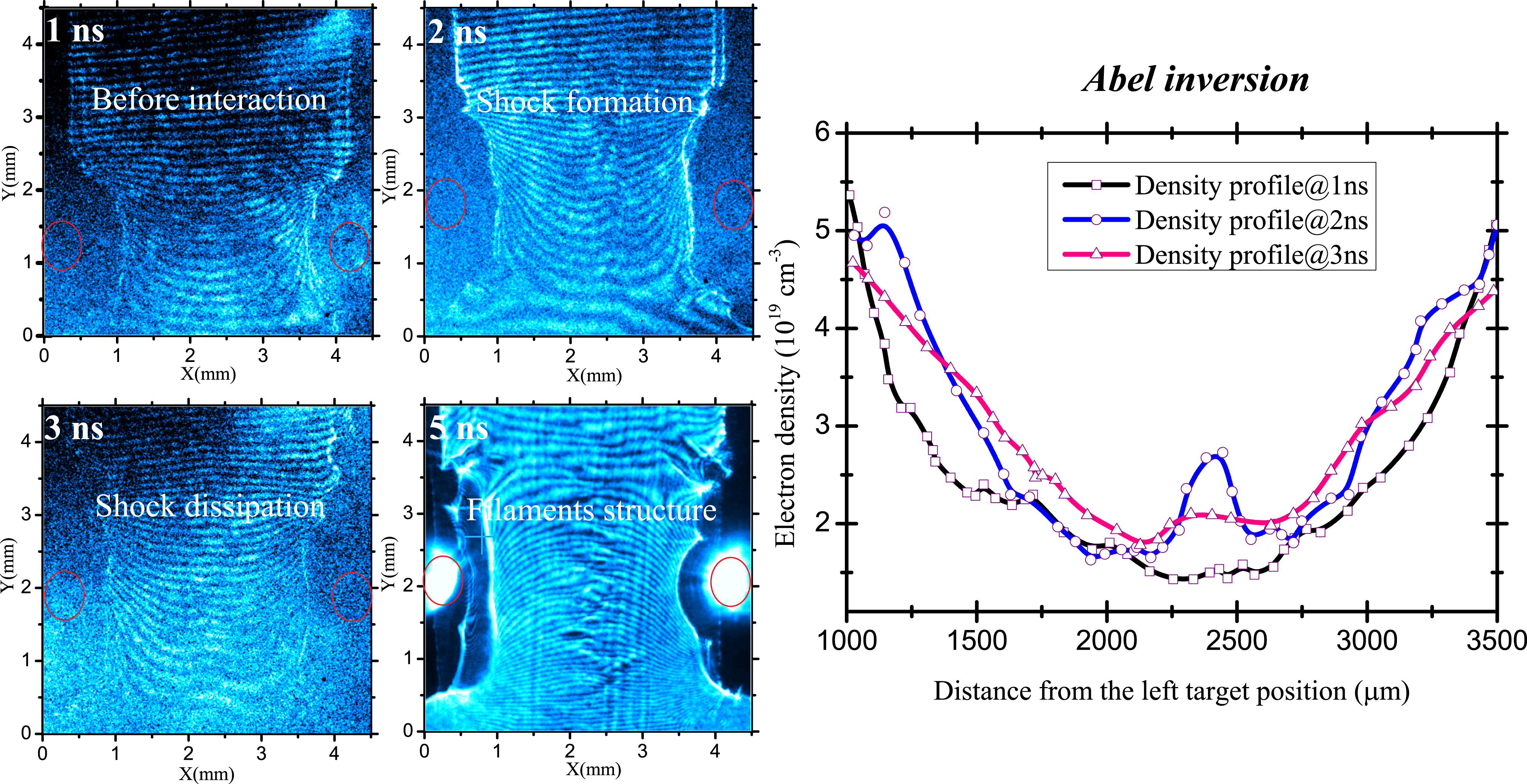
Figure 2. The evolution of the counter-streaming flows obtained by a Nomarski interferometer. The red circle in the raw images stands for the laser focal spot. When both flows coming from the opposing foils interpenetrate each other at the midplane at 2 ns shown in Abel inversion image, the plasma density increases by the unanticipated factor of 3 (from
![]() $1\times 10^{19}~\text{cm}^{-3}$
to
$1\times 10^{19}~\text{cm}^{-3}$
to
![]() $2.8\times 10^{19}~\text{cm}^{-3}$
), indicating that a shock has been generated. The width is measured as about
$2.8\times 10^{19}~\text{cm}^{-3}$
), indicating that a shock has been generated. The width is measured as about
![]() $300~\unicode[STIX]{x03BC}\text{m}$
, much smaller than the MFPs. Obviously, it is collisionless. Subsequently (
$300~\unicode[STIX]{x03BC}\text{m}$
, much smaller than the MFPs. Obviously, it is collisionless. Subsequently (
![]() ${\sim}3{-}5~\text{ns}$
), the collisionless shock is dissipated by the growing filamentation structures.
${\sim}3{-}5~\text{ns}$
), the collisionless shock is dissipated by the growing filamentation structures.
Relevant works[Reference Stockem, Fiuza, Bret, Fonseca and Silva25, Reference Kato and Takabe26] show that two candidate instabilities can be self-generated under such experimental conditions (
![]() $n_{e}\sim 10^{19}~\text{cm}^{-3}$
,
$n_{e}\sim 10^{19}~\text{cm}^{-3}$
,
![]() $\unicode[STIX]{x1D710}\sim 10^{8}~\text{cm}\cdot \text{s}^{-1}$
,
$\unicode[STIX]{x1D710}\sim 10^{8}~\text{cm}\cdot \text{s}^{-1}$
,
![]() $T_{e}\sim 0.2{-}1~\text{keV}$
). One is electrostatic instability [Reference Forslund and Shonk27], and the other one is Weibel-type/filamentation instability[Reference Weibel28, Reference Fox, Fiksel, Bhattacharjee, Chang, Germaschewski, Hu and Nilson29]. Simulation results show that both instabilities are competitive. The filamentation instability developed later would destroy the evolution of the electrostatic instability[Reference Kato and Takabe26]. This evolution is consistent with the observed experimental results. In order to measure the whole process of the ES, we should suppress the growth of the Weibel-type instability. According to the growth rate of the Weibel-type instability,
$T_{e}\sim 0.2{-}1~\text{keV}$
). One is electrostatic instability [Reference Forslund and Shonk27], and the other one is Weibel-type/filamentation instability[Reference Weibel28, Reference Fox, Fiksel, Bhattacharjee, Chang, Germaschewski, Hu and Nilson29]. Simulation results show that both instabilities are competitive. The filamentation instability developed later would destroy the evolution of the electrostatic instability[Reference Kato and Takabe26]. This evolution is consistent with the observed experimental results. In order to measure the whole process of the ES, we should suppress the growth of the Weibel-type instability. According to the growth rate of the Weibel-type instability,
we have two methods to adjust the Weibel-type instability. One is symmetrical case (Case I), replacing the target material, i.e., changing the value,
![]() $(Z/A)\sqrt{f}$
. The other one is unsymmetrical case (Case II), changing the driven laser energy
$(Z/A)\sqrt{f}$
. The other one is unsymmetrical case (Case II), changing the driven laser energy
![]() $E_{L}$
. Here we define the symmetrical case and unsymmetrical case according to the driven laser conditions instead of the plasma flow conditions. The symmetrical case stands for two bunches heating the target foils, and the unsymmetrical case stands for only one bunch heating the target foil.
$E_{L}$
. Here we define the symmetrical case and unsymmetrical case according to the driven laser conditions instead of the plasma flow conditions. The symmetrical case stands for two bunches heating the target foils, and the unsymmetrical case stands for only one bunch heating the target foil.
2.2 Collisionless electrostatic shock formation and evolution in the CPFs
2.2.1 Unsymmetrical case
Figure 3 shows the ES in the CPFs at 5 ns and 9 ns[Reference Morita, Sakawa, Kuramitsu, Dono, Aoki, Tanji, Kato, Li, Zhang, Liu, Zhong, Takabe and Zhang30]. In this experiment configuration, the laser-driven high-velocity, low-density left flow interacts with the low-velocity, high-density flow generated by X-ray ionization at the surface of the right foil. Both flow densities are measured by the interferograms, i.e.,
![]() $n_{e}^{\text{Left}}\sim 2\times 10^{18}~\text{cm}^{-3}$
and
$n_{e}^{\text{Left}}\sim 2\times 10^{18}~\text{cm}^{-3}$
and
![]() $n_{e}^{\text{Right}}\sim 6\times 10^{18}~\text{cm}^{-3}$
. Some structures appear near to
$n_{e}^{\text{Right}}\sim 6\times 10^{18}~\text{cm}^{-3}$
. Some structures appear near to
![]() $x=3.6{-}3.7~\text{mm}$
at 5 ns, indicating that both flow velocities can be estimated as
$x=3.6{-}3.7~\text{mm}$
at 5 ns, indicating that both flow velocities can be estimated as
![]() $\unicode[STIX]{x1D710}^{\text{Left}}\sim 830~\text{km}\cdot \text{s}^{-1}$
and
$\unicode[STIX]{x1D710}^{\text{Left}}\sim 830~\text{km}\cdot \text{s}^{-1}$
and
![]() $\unicode[STIX]{x1D710}^{\text{Right}}\sim 230~\text{km}\cdot \text{s}^{-1}$
. The corresponding MFPs are calculated as 25–35 mm, confirming that both flows interaction is collisionless. These observed structures at 5 ns in Figures 3(a) and 3(c) are identified as a large-density jump. However, its value is difficult to measure because of such a larger density gradient blocking the probe propagation. Anyway, such a large-density jump indicates that a collisionless shock has been generated at 5 ns. With the development of the shock, it continues to move from
$\unicode[STIX]{x1D710}^{\text{Right}}\sim 230~\text{km}\cdot \text{s}^{-1}$
. The corresponding MFPs are calculated as 25–35 mm, confirming that both flows interaction is collisionless. These observed structures at 5 ns in Figures 3(a) and 3(c) are identified as a large-density jump. However, its value is difficult to measure because of such a larger density gradient blocking the probe propagation. Anyway, such a large-density jump indicates that a collisionless shock has been generated at 5 ns. With the development of the shock, it continues to move from
![]() $x=3.6{-}3.7~\text{mm}$
at 5 ns to
$x=3.6{-}3.7~\text{mm}$
at 5 ns to
![]() $x=3.1~\text{mm}$
at 9 ns, i.e., it propagates with a velocity of
$x=3.1~\text{mm}$
at 9 ns, i.e., it propagates with a velocity of
![]() $\unicode[STIX]{x1D710}_{s}\sim 125{-}150~\text{km}\cdot \text{s}^{-1}$
. The corresponding Mach number is about 9–11, suggesting a strong collisionless shock formation. The typical features of the shock at 9 ns are shown in Figures 3(e) and 3(f), and the density jump decreases to
$\unicode[STIX]{x1D710}_{s}\sim 125{-}150~\text{km}\cdot \text{s}^{-1}$
. The corresponding Mach number is about 9–11, suggesting a strong collisionless shock formation. The typical features of the shock at 9 ns are shown in Figures 3(e) and 3(f), and the density jump decreases to
![]() $n_{\text{shock}}/n_{\text{flow}}\sim 3.89\pm 0.85$
with the whole transition region of about
$n_{\text{shock}}/n_{\text{flow}}\sim 3.89\pm 0.85$
with the whole transition region of about
![]() $200~\unicode[STIX]{x03BC}\text{m}$
.
$200~\unicode[STIX]{x03BC}\text{m}$
.
To clarify the generation mechanism of the shock, a quasi-one-dimensional particle-in-cell (PIC) simulation is performed under the same experimental conditions. From Figure 4 in Ref. [Reference Morita, Sakawa, Kuramitsu, Dono, Aoki, Tanji, Kato, Li, Zhang, Liu, Zhong, Takabe and Zhang30], a self-generated bipolar electrostatic field mediated shock formation appears at
![]() $x/\unicode[STIX]{x1D706}_{e}\sim 26$
in the beginning, and then propagates toward
$x/\unicode[STIX]{x1D706}_{e}\sim 26$
in the beginning, and then propagates toward
![]() $\pm x$
directions. The incoming ions will be slowed down or reflected back into upstream. Consequently, ions are accumulated into the interaction region until the density jump conditions are fulfilled[Reference Morita, Sakawa, Kuramitsu, Dono, Aoki, Tanji, Kato, Li, Zhang, Liu, Zhong, Takabe and Zhang30, Reference Sakawa, Morita, Kuramitsu and Takabe31].
$\pm x$
directions. The incoming ions will be slowed down or reflected back into upstream. Consequently, ions are accumulated into the interaction region until the density jump conditions are fulfilled[Reference Morita, Sakawa, Kuramitsu, Dono, Aoki, Tanji, Kato, Li, Zhang, Liu, Zhong, Takabe and Zhang30, Reference Sakawa, Morita, Kuramitsu and Takabe31].
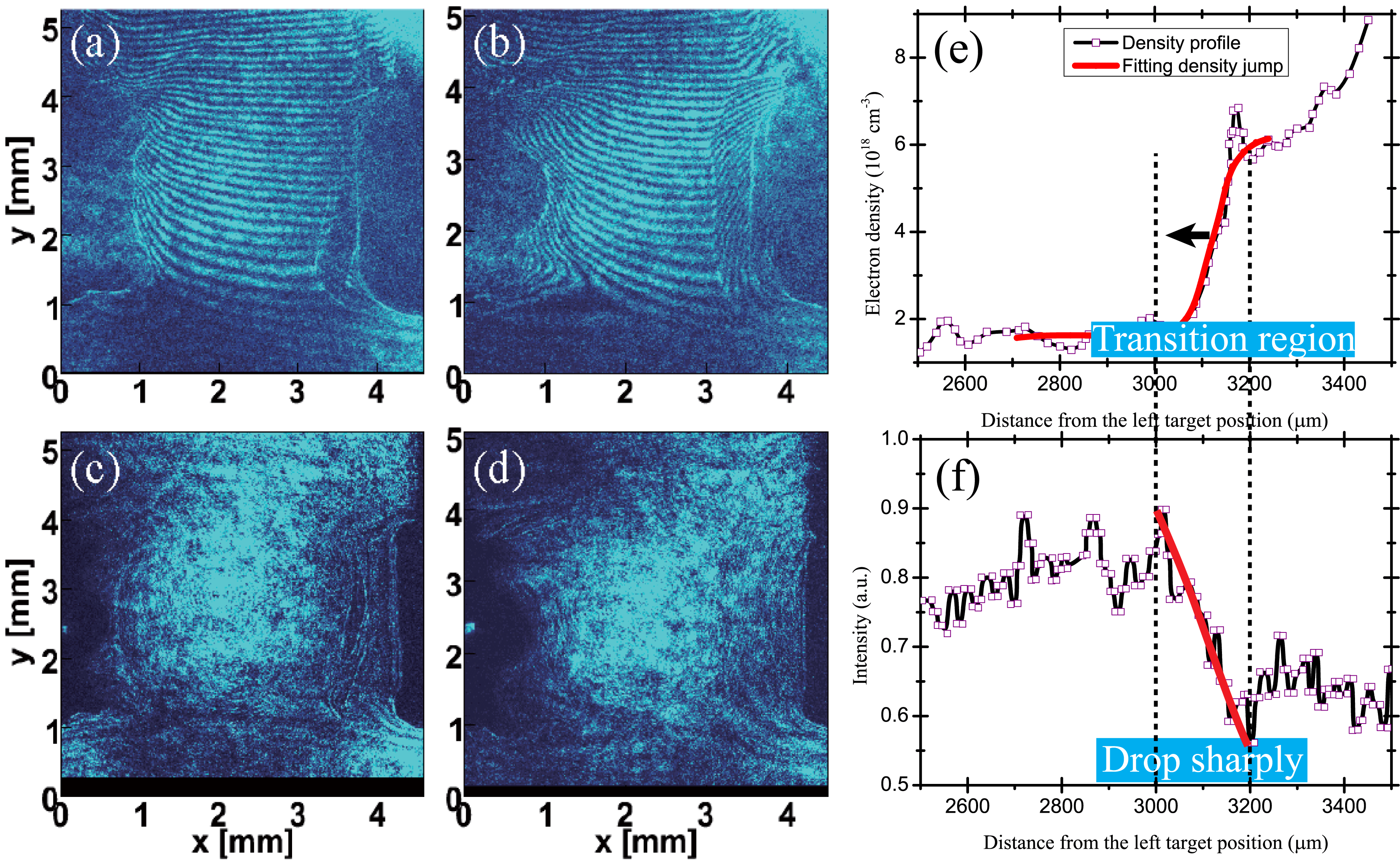
Figure 3. Collisionless shock formation and evolution in unsymmetrical CPFs[Reference Morita, Sakawa, Kuramitsu, Dono, Aoki, Tanji, Kato, Li, Zhang, Liu, Zhong, Takabe and Zhang30]. (a) and (b) show the interferogram obtained at 5 ns and 9 ns, respectively. (c) and (d) are the corresponding shadowgraphs of (a) and (b). (e) and (f) show the density profile and the intensity profile at 9 ns.
2.2.2 Symmetrical case
Figure 4 shows the ES formation and evolution in the CPFs at 6 ns and 10 ns. The CH target material is replaced by the Cu. In this experiment configuration, two similar laser-produced plasma flows interact with each other (
![]() $n_{e}\sim 1\times 10^{19}~\text{cm}^{-3}$
,
$n_{e}\sim 1\times 10^{19}~\text{cm}^{-3}$
,
![]() $2\unicode[STIX]{x1D710}\sim 7.5\times 10^{7}~\text{cm}\cdot \text{s}^{-1}$
). Two overlapped shocks are formed in the central region and then evolve into two separated shocks from the downstream to upstream. The MFP (16–500 mm) is also much larger than the shock width (
$2\unicode[STIX]{x1D710}\sim 7.5\times 10^{7}~\text{cm}\cdot \text{s}^{-1}$
). Two overlapped shocks are formed in the central region and then evolve into two separated shocks from the downstream to upstream. The MFP (16–500 mm) is also much larger than the shock width (
![]() $400{-}700~\unicode[STIX]{x03BC}\text{m}$
). According to the heuristic model proposed by Park et al. in Ref. [Reference Park, Ryutov, Ross, Kugland, Glenzer, Plechaty, Pollaine, Remington, Spitkovsky, Gargate, Gregori, Bell, Murphy, Sakawa, Kuramitsu, Morita, Takabe, Froula, Fiksel, Miniati, Koenig, Ravasio, Pelka, Liang, Woolsey, Kuranz, Drake and Grosskopf32], the width of the ES transition region can be estimated as
$400{-}700~\unicode[STIX]{x03BC}\text{m}$
). According to the heuristic model proposed by Park et al. in Ref. [Reference Park, Ryutov, Ross, Kugland, Glenzer, Plechaty, Pollaine, Remington, Spitkovsky, Gargate, Gregori, Bell, Murphy, Sakawa, Kuramitsu, Morita, Takabe, Froula, Fiksel, Miniati, Koenig, Ravasio, Pelka, Liang, Woolsey, Kuranz, Drake and Grosskopf32], the width of the ES transition region can be estimated as
![]() $L_{ES}=K\frac{\unicode[STIX]{x1D710}}{\unicode[STIX]{x1D714}_{pi}}\frac{W}{T_{e}}\approx (600{-}800)~\unicode[STIX]{x03BC}\text{m}$
, in agreement with our measurement (
$L_{ES}=K\frac{\unicode[STIX]{x1D710}}{\unicode[STIX]{x1D714}_{pi}}\frac{W}{T_{e}}\approx (600{-}800)~\unicode[STIX]{x03BC}\text{m}$
, in agreement with our measurement (
![]() $L\sim 450{-}800~\unicode[STIX]{x03BC}\text{m}$
). However, the width of the Weibel-type shock should be estimated as
$L\sim 450{-}800~\unicode[STIX]{x03BC}\text{m}$
). However, the width of the Weibel-type shock should be estimated as
![]() $L_{EM}=K\frac{\unicode[STIX]{x1D710}}{\unicode[STIX]{x1D714}_{pi}}\approx 15~\text{mm}$
, much larger than our target separation. The theoretical analysis shows that the observed shocks should be electrostatic. The corresponding PIC simulations also confirm our understanding. As shown in Figure 5 in Ref. [Reference Yuan, Li, Liu, Zhong, Zhu, Li, Wei, Han, Pei, Zhao, Li, Zhang, Liang, Wang, Weng, Li, Jiang, Du, Ding, Zhu, Zhu, Zhao and Zhang20], a strong bipolar electrostatic field resulted from the instability excites the shocks. Large temperature and density gradients between upstream and downstream drive the shock from downstream to upstream.
$L_{EM}=K\frac{\unicode[STIX]{x1D710}}{\unicode[STIX]{x1D714}_{pi}}\approx 15~\text{mm}$
, much larger than our target separation. The theoretical analysis shows that the observed shocks should be electrostatic. The corresponding PIC simulations also confirm our understanding. As shown in Figure 5 in Ref. [Reference Yuan, Li, Liu, Zhong, Zhu, Li, Wei, Han, Pei, Zhao, Li, Zhang, Liang, Wang, Weng, Li, Jiang, Du, Ding, Zhu, Zhu, Zhao and Zhang20], a strong bipolar electrostatic field resulted from the instability excites the shocks. Large temperature and density gradients between upstream and downstream drive the shock from downstream to upstream.

Figure 4. Collisionless shock formation and evolution in the symmetrical CPFs. (a) and (b) are the interferograms (lower) and electron density distributions (upper) obtained by the Abel inversion, taken at 6 ns and 10 ns, respectively. (c) and (d) are the electron density profiles plotted along the flow direction[Reference Yuan, Li, Liu, Zhong, Zhu, Li, Wei, Han, Pei, Zhao, Li, Zhang, Liang, Wang, Weng, Li, Jiang, Du, Ding, Zhu, Zhu, Zhao and Zhang20].
2.3 Weibel/filamentation instability in the symmetrical case
Weibel instability is a promising candidate for creating astrophysical shocks. It is a typical electromagnetic phenomenon, driven by the plasma anisotropy. Under the current laser-plasma conditions, i.e., the electron thermal velocity is larger than the flow velocity and the ion thermal velocity is smaller than the flow velocity, the ions freely interpenetrate each other in the presence of a single thermalized electron background. Therefore, it is called ion–ion driven Weibel-type instability. The signature of Weibel instability is that the filamentary structures form and extend in the axis of flow direction. The self-generated magnetic field grows from linear phase to nonlinear phase until saturation. Although many groups[Reference Fox, Fiksel, Bhattacharjee, Chang, Germaschewski, Hu and Nilson29, Reference Ross, Higginson, Ryutov, Fiuza, Hatarik, Huntington, Kalantar, Link, Pollock, Remington, Rinderknecht, Swadling, Turnbull, Weber, Wilks, Froula, Rosenberg, Morita, Sakawa, Takabe, Drake, Kuranz, Gregori, Meinecke, Levy, Koenig, Spitkovsky, Petrasso, Li, Sio, Lahmann, Zylstra and Park33–Reference Huntington, Manuel, Ross, Wilks, Fiuza, Rinderknecht, Park, Gregori, Higginson, Park, Pollock, Remington, Ryutov, Ruyer, Sakawa, Sio, Spitkovsky, Swadling, Takabe and Zylstra35] have been devoted into investigation of the Weibel-mediated shock formation, the required exact physical conditions for such an occurrence are still unclear.
According to Equation (1), we can find that increasing the flow velocity and density can enhance the growth rate of the Weibel instability. Here we demonstrate the Weibel instability in CPFs generated by CH–Al foils. Figure 5 shows the typical results of evolution of the Weibel-type instability. The left flow (in the interferogram) is generated by one bunch ablation of CH foil, and the right flow is generated by the other bunch ablation of Al foil. Such a configuration can produce a relatively high density (
![]() $n_{e}\sim 3\times 10^{19}~\text{cm}^{-3}$
) and similar velocity (
$n_{e}\sim 3\times 10^{19}~\text{cm}^{-3}$
) and similar velocity (
![]() $\unicode[STIX]{x1D710}\sim 0.8\times 10^{8}~\text{cm}\cdot \text{s}^{-1}$
) plasma flows, in comparison with CH–CH case in Figure 2 (
$\unicode[STIX]{x1D710}\sim 0.8\times 10^{8}~\text{cm}\cdot \text{s}^{-1}$
) plasma flows, in comparison with CH–CH case in Figure 2 (
![]() $n_{e}\sim 1\times 10^{19}~\text{cm}^{-3}$
,
$n_{e}\sim 1\times 10^{19}~\text{cm}^{-3}$
,
![]() $\unicode[STIX]{x1D710}\sim 1\times 10^{8}~\text{cm}\cdot \text{s}^{-1}$
). The typical features of the Weibel instability can be observed in the shadowgraph. At 3.5 ns, periodically distributing filaments parallel to flow direction localize at the midplane with a wavelength (
$\unicode[STIX]{x1D710}\sim 1\times 10^{8}~\text{cm}\cdot \text{s}^{-1}$
). The typical features of the Weibel instability can be observed in the shadowgraph. At 3.5 ns, periodically distributing filaments parallel to flow direction localize at the midplane with a wavelength (
![]() $\unicode[STIX]{x1D706}$
) of about
$\unicode[STIX]{x1D706}$
) of about
![]() $50{-}80~\unicode[STIX]{x03BC}\text{m}$
. The wavelength is almost consistent with the ion inertial scale,
$50{-}80~\unicode[STIX]{x03BC}\text{m}$
. The wavelength is almost consistent with the ion inertial scale,
![]() $d_{i}=c/\unicode[STIX]{x1D714}_{pi}=c/\sqrt{4\unicode[STIX]{x1D70B}n_{i}\bar{Z}^{2}e^{2}/m_{i}}\approx 70{-}80~\unicode[STIX]{x03BC}\text{m}$
(here the used flows density is
$d_{i}=c/\unicode[STIX]{x1D714}_{pi}=c/\sqrt{4\unicode[STIX]{x1D70B}n_{i}\bar{Z}^{2}e^{2}/m_{i}}\approx 70{-}80~\unicode[STIX]{x03BC}\text{m}$
(here the used flows density is
![]() $n_{e}\sim (2{-}3)\times 10^{19}~\text{cm}^{-3}$
and
$n_{e}\sim (2{-}3)\times 10^{19}~\text{cm}^{-3}$
and
![]() $\bar{Z}\sim 10$
), indicating that the instability is driven by the ions. The linear growth rate of the filamentation instability is approximated to be
$\bar{Z}\sim 10$
), indicating that the instability is driven by the ions. The linear growth rate of the filamentation instability is approximated to be
![]() $\unicode[STIX]{x1D6FE}\approx 0.2\unicode[STIX]{x1D710}/\unicode[STIX]{x1D706}=(2{-}3)\times 10^{9}~\text{s}^{-1}$
. The corresponding linear time of the filaments is about 2–3 ns (
$\unicode[STIX]{x1D6FE}\approx 0.2\unicode[STIX]{x1D710}/\unicode[STIX]{x1D706}=(2{-}3)\times 10^{9}~\text{s}^{-1}$
. The corresponding linear time of the filaments is about 2–3 ns (
![]() $t=2\unicode[STIX]{x1D70B}/\unicode[STIX]{x1D6FE}$
), after both flows meeting at the midplane. At 4.5 ns, with the growth of instability, the filaments extend longer in the axial direction. The average space between adjacent filaments becomes
$t=2\unicode[STIX]{x1D70B}/\unicode[STIX]{x1D6FE}$
), after both flows meeting at the midplane. At 4.5 ns, with the growth of instability, the filaments extend longer in the axial direction. The average space between adjacent filaments becomes
![]() $100{-}120~\unicode[STIX]{x03BC}\text{m}$
, indicating that the coalescence process between adjacent filaments occurs and the instability evolves from the linear mode into the nonlinear mode. At 6.5 ns, the larger wavelength of order
$100{-}120~\unicode[STIX]{x03BC}\text{m}$
, indicating that the coalescence process between adjacent filaments occurs and the instability evolves from the linear mode into the nonlinear mode. At 6.5 ns, the larger wavelength of order
![]() $150{-}180~\unicode[STIX]{x03BC}\text{m}$
and disordered filaments at the midplane reveal that the instability has fully evolved into the nonlinear mode. The experimental evolution of the Weibel instability is consistent with the theoretical prediction.
$150{-}180~\unicode[STIX]{x03BC}\text{m}$
and disordered filaments at the midplane reveal that the instability has fully evolved into the nonlinear mode. The experimental evolution of the Weibel instability is consistent with the theoretical prediction.
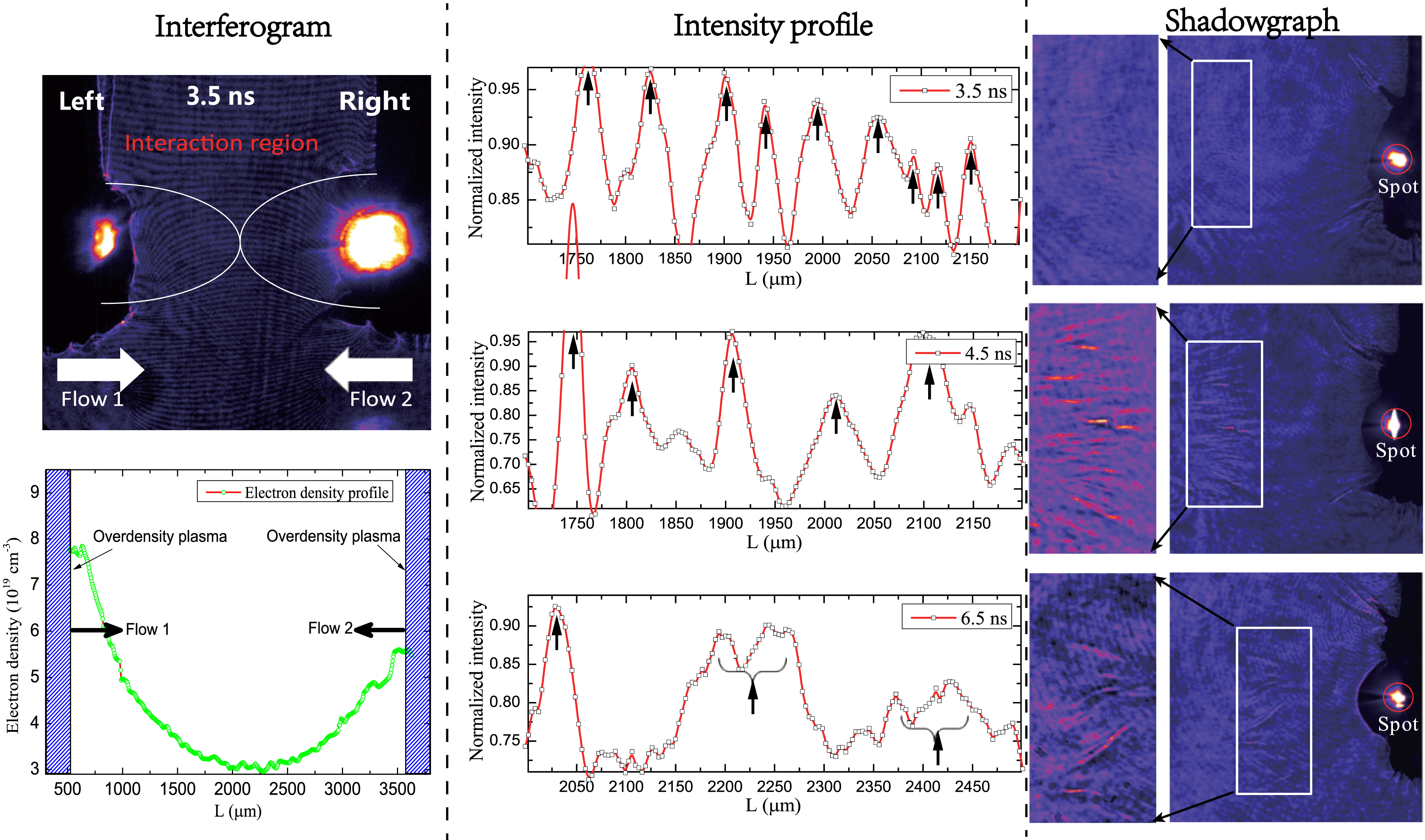
Figure 5. The evolution of the filamentation instability in CPFs. Interferogram with magnification of 2.5 times shows initial conditions of both flows at 3.5 ns. A series of shadowgraph with larger magnification of 4 times is applied to measure the evolution of the Weibel instability. The intensity profile shows the typical features of the evolution of the filaments.
2.4 Other applications of the CPFs
The neutron yield in CPFs is an important tool to distinguish between collisionless and collisional effects. Neutrons generation in CPFs can originate from three sources: (i) the laser-induced fireballs from the target foils, (ii) the counter-propagating ions interaction with each other, and (iii) the scattering ions interaction with the ions from intra-flows. Here we carry out two neutron generation experiments for comparison[Reference Zhao, Chen, Li, Fu, Rhee, Li, Zhu, Li, Liao, Zhang, Han, Liu, Huang, Ma, Li, Xiong, Huang, Fu, Zhu, Zhao and Zhang36]. One is for collisionless case (foil targets)—high-velocity, low-density counter-streaming flows—and the other one is collisional case (K-shaped targets)—low-velocity, high-density counter-streaming jets. The neutrons of 2.45 MeV are produced by deuterium–deuterium (DD) nuclear reactions (
![]() $\text{D}+\text{D}\rightarrow 3\text{He}+n(2.45~\text{MeV})$
). The typical signal of the 2.45 MeV neutrons is shown in Figure 6. Since the nuclear cross section changes sharply at the limits of 2 MeV of incident ions, it can be regarded as similar for both cases at the typically laser-produced flow velocity region (
$\text{D}+\text{D}\rightarrow 3\text{He}+n(2.45~\text{MeV})$
). The typical signal of the 2.45 MeV neutrons is shown in Figure 6. Since the nuclear cross section changes sharply at the limits of 2 MeV of incident ions, it can be regarded as similar for both cases at the typically laser-produced flow velocity region (
![]() $10^{7}{-}10^{8}~\text{cm}\cdot \text{s}^{-1}$
). However, the density difference is very large. From the optical measurement, we can find that the flows are with density of
$10^{7}{-}10^{8}~\text{cm}\cdot \text{s}^{-1}$
). However, the density difference is very large. From the optical measurement, we can find that the flows are with density of
![]() $10^{19}~\text{cm}^{-3}$
, while the jets are with density larger than
$10^{19}~\text{cm}^{-3}$
, while the jets are with density larger than
![]() $10^{21}~\text{cm}^{-3}$
(roughly
$10^{21}~\text{cm}^{-3}$
(roughly
![]() $n_{jet}\sim 100n_{\text{flow}}$
). When we compare both cases, we can find that the neutron yields in collisional case (
$n_{jet}\sim 100n_{\text{flow}}$
). When we compare both cases, we can find that the neutron yields in collisional case (
![]() $10^{6}$
)[Reference Zhao, Chen, Li, Fu, Rhee, Li, Zhu, Li, Liao, Zhang, Han, Liu, Huang, Ma, Li, Xiong, Huang, Fu, Zhu, Zhao and Zhang36] is only 5–10 times as much as that in collisionless case (
$10^{6}$
)[Reference Zhao, Chen, Li, Fu, Rhee, Li, Zhu, Li, Liao, Zhang, Han, Liu, Huang, Ma, Li, Xiong, Huang, Fu, Zhu, Zhao and Zhang36] is only 5–10 times as much as that in collisionless case (
![]() $(1{-}5)\times 10^{5}$
)[Reference Zhang, Zhao, Yuan, Fu, Bao, Chen, He, Hou, Li, Li, Li, Liao, Rhee, Sun, Xu, Zhao, Zhu, Zhu, Zhang and Zhang37]. One possible explanation is that the ions scattered by the self-generated electromagnetic field interaction with the ions from intra-flows will effectively enhance the neutron yields. This laser-produced CPF provides us not only a new tool to distinguish Coulomb collisions from the collisionless effects, i.e., random electromagnetic fields originated from instabilities, but also a platform for studying the nuclear astrophysics, such as the abundance of the
$(1{-}5)\times 10^{5}$
)[Reference Zhang, Zhao, Yuan, Fu, Bao, Chen, He, Hou, Li, Li, Li, Liao, Rhee, Sun, Xu, Zhao, Zhu, Zhu, Zhang and Zhang37]. One possible explanation is that the ions scattered by the self-generated electromagnetic field interaction with the ions from intra-flows will effectively enhance the neutron yields. This laser-produced CPF provides us not only a new tool to distinguish Coulomb collisions from the collisionless effects, i.e., random electromagnetic fields originated from instabilities, but also a platform for studying the nuclear astrophysics, such as the abundance of the
![]() $^{26}$
Al[Reference Prantzos and Diehl38] and
$^{26}$
Al[Reference Prantzos and Diehl38] and
![]() $^{6,7}$
Li[Reference Cyburt, Fields, Olive and Yeh39].
$^{6,7}$
Li[Reference Cyburt, Fields, Olive and Yeh39].
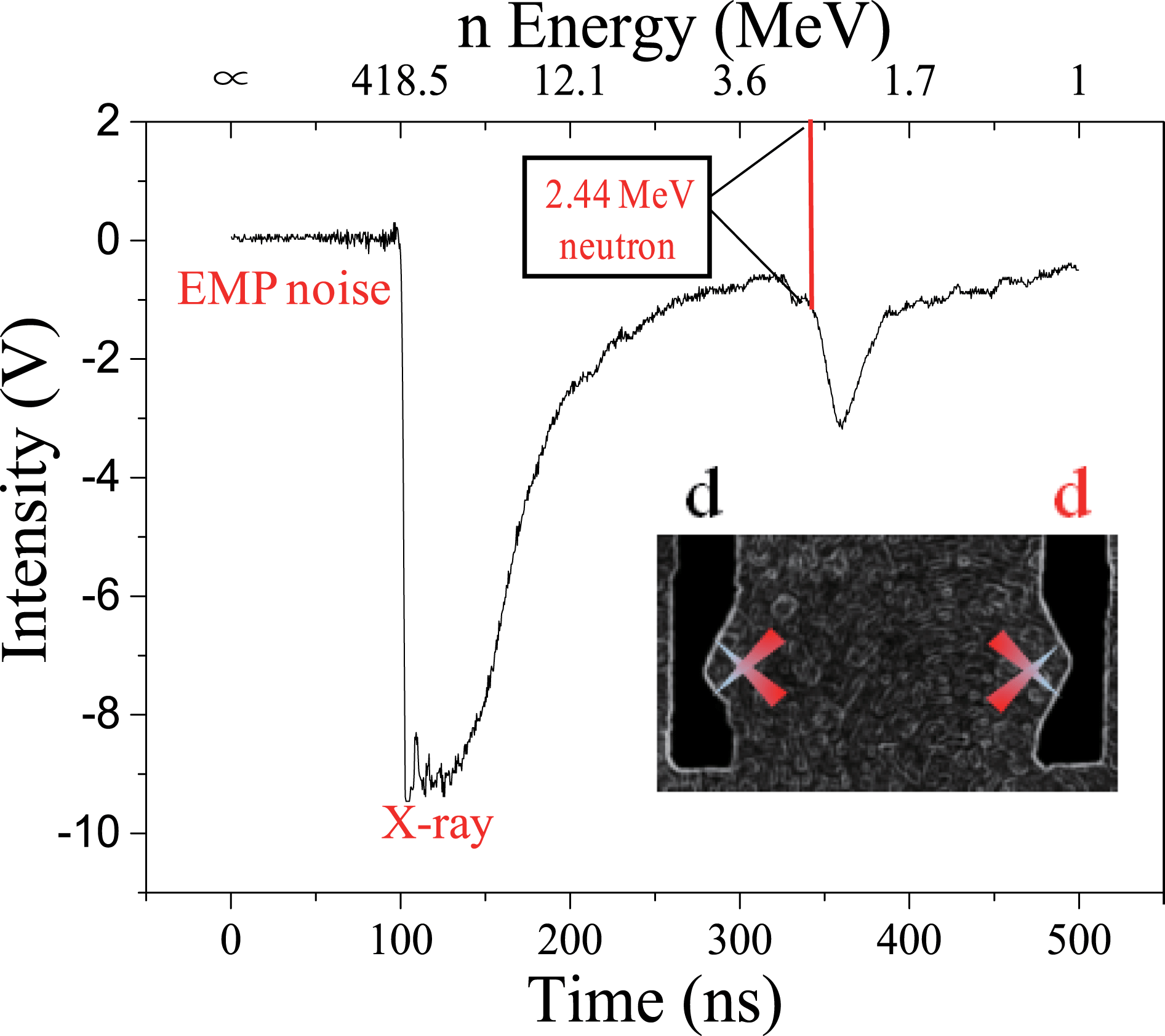
Figure 6. The observed neutron signals from D–D nuclear reaction in collisional case[Reference Zhao, Chen, Li, Fu, Rhee, Li, Zhu, Li, Liao, Zhang, Han, Liu, Huang, Ma, Li, Xiong, Huang, Fu, Zhu, Zhao and Zhang36, Reference Zhao, Zhang, Yuan, Li, Li, Rhee, Zhang, Li, Zhu, Li, Han, Liu, Ma, Li, Tao, Li, Guo, Huang, Fu, Zhu, Zhao, Chen, Fu and Zhang40].
3 Summary and outlook
The study of astrophysical shock formation is important for us to understand the particle acceleration and cosmic rays generation. The laboratory experiments provide us a new opportunity to investigate the physical mechanism behind these scenarios. Our experimental results show that both electrostatic instability and filamentation instability can grow up in CPFs, but compete with each other. The self-generated bipolar electrostatic field from the electrostatic instability can support the shock formation and evolution. However, the magnetic field is too weak to excite the shock generation.
Considering the characteristic of the cosmic ray spectrum with power law, Weibel-mediated shock is a promising candidate via diffusive shock acceleration. Such important issues of the acceleration mechanism are not fully understood and still a big challenge. A stronger magnetic field is necessary to excite the Weibel-type shock. This higher magnetic field could be achieved by optimizing filamentation instability[Reference Park, Huntington, Fiuza, Drake, Froula, Gregori, Koenig, Kugland, Kuranz, Lamb, Levy, Li, Meinecke, Morita, Petrasso, Pollock, Remington, Rinderknecht, Rosenberg, Ross, Ryutov, Sakawa, Spitkovsky, Takabe, Turnbull, Tzeferacos, Weber and Zylstra34, Reference Huntington, Manuel, Ross, Wilks, Fiuza, Rinderknecht, Park, Gregori, Higginson, Park, Pollock, Remington, Ryutov, Ruyer, Sakawa, Sio, Spitkovsky, Swadling, Takabe and Zylstra35] or laser-driven coils[Reference Fujioka, Zhang, Ishihara, Shigemori, Hironaka, Johzaki, Sunahara, Yamamoto, Nakashima, Watanabe, Shiraga, Nishimura and Azechi41–Reference Zhu, Li, Yuan, Li, Li, Liao, Zhao, Zhong, Xue, He, Wang, Lu, Zhang, Yang, Zhou, Xie, Hong, Wei, Zhang, Han, Pei, Liu, Zhang, Wang, Zhu, Gu, Zhao, Zhang, Zhao and Zhang43] in future experiments.
Acknowledgements
The authors thank the staff of the SG-II laser facility for operating the laser and target area. This work is supported by the Science Challenge Project (No. TZ2016005), the National Basic Program of China (No. 2013CBA01501/03), the National Natural Science Foundation of China (Nos. 11503041, 11522326, 11622323, and 11573040), the Strategic Priority Research Program of the Chinese Academy of Sciences (Nos. XDB16010200 and XDB07030300), and the Project Funded by China Postdoctoral Science Foundation (No. 2015M571124).







