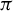1 Introduction
Controlled fusion is considered a viable method for generating electricity by harnessing the heat from nuclear reactions. Inertial confinement fusion (ICF)[ Reference Nuckolls, Wood and Thiessen1– Reference Lindl3] is one of the promising schemes for achieving fusion energy gain. In ICF, multiple high-energy lasers are used to directly irradiate the target (known as the ‘direct-drive’ scheme) or indirectly ablate the target through X-rays from the laser-heated hohlraum (‘indirect-drive’ scheme), to drive spherical implosions via the rocket effect. The symmetrically imploding deuterium-tritium (DT) fuel is then compressed, and a high-density and high-temperature core is eventually formed to ignite the entire target. For a high-performance implosion, the efficiency and uniformity of the laser energy deposition are of primary concern. During laser–plasma interactions, a part of the laser energy is diverted through laser–plasma instabilities (LPIs)[ Reference Froula, Michel, Igumenshchev, Hu, Yaakobi, Myatt, Edgell, Follett, Glebov, Goncharov, Kessler, Maximov, Radha, Sangster, Seka, Short, Solodov, Sorce and Stoeckl4], degrading the laser absorption and hydrodynamic efficiency, which need to be strategically mitigated. In parametric three-wave processes, including stimulated Brillouin scattering (SBS)[ Reference Seka, Baldis, Fuchs, Regan, Meyerhofer, Stoeckl, Yaakobi, Craxton and Short5, Reference Liu, Rosenbluth and White6] and stimulated Raman scattering (SRS)[ Reference Michel, Rosenberg, Seka, Solodov, Short, Chapman, Goyon, Lemos, Hohenberger, Moody, Regan and Myatt7, Reference Short8], the energy of the incident laser beams can be scattered off through interactions with plasma waves. Besides, suprathermal electrons generated by high-amplitude electron plasma waves from two-plasmon decay (TPD)[ Reference Christopherson, Betti, Forrest, Howard, Theobald, Delettrez, Rosenberg, Solodov, Stoeckl, Patel, Gopalaswamy, Cao, Peebles, Edgell, Seka, Epstein, Wei, Johnson, Simpson, Regan and Campbell9, Reference Christopherson, Betti, Forrest, Howard, Theobald, Campbell, Delettrez, Rosenberg, Solodov, Stoeckl, Patel, Gopalaswamy, Cao, Peebles, Edgell, Seka, Epstein, Scullin, Radha, Wei, Regan, Johnson and Simpson10] or SRS[ Reference Trela, Theobald, Anderson, Batani, Betti, Casner, Delettrez, Frenje, Glebov, Ribeyre, Solodov, Stoeckl and Stoeckl11] may have a great impact on implosion performance by preheating the fuel and restricting the compressed density. Furthermore, multi-beam LPI processes such as crossed-beam energy transfer (CBET)[ Reference Igumenshchev, Seka, Edgell, Michel, Froula, Goncharov, Craxton, Divol, Epstein, Follett, Kelly, Kosc, Maximov, McCrory, Meyerhofer, Michel, Myatt, Sangster, Shvydky, Skupsky and Stoeckl12, Reference Marozas, Hohenberger, Rosenberg, Turnbull, Collins, Radha, McKenty, Zuegel, Marshall and Regan13] and TPD[ Reference Seka, Edgell, Myatt, Maximov, Short, Goncharov and Baldis14– Reference Simon, Short, Williams and Dewandre16] could redistribute energy absorption and beam power balance. Due to the importance of LPI physics, precise and comprehensive diagnostics for laser absorption are vital in evaluating implosion performance and implementing various strategies to mitigate energy losses, especially in the direct-drive approach where target implosions are directly driven by laser ablation.
To diagnose laser absorption, a straightforward method is to measure laser lights that remain unabsorbed but scattered (including refraction and reflection) from the target. Full-aperture backscatter stations (FABSs)[ Reference Moody, Datte, Krauter, Bond, Michel, Glenzer, Divol, Niemann, Suter, Meezan, MacGowan, Hibbard, London, Kilkenny, Wallace, Kline, Knittel, Frieders, Golick, Ross, Widmann, Jackson, Vernon and Clancy17] are commonly used to measure backward scattered lights. For side SRS, which has been found to be important in direct-drive programs[ Reference Rosenberg, Solodov, Myatt, Seka, Michel, Hohenberger, Short, Epstein, Regan, Campbell, Chapman, Goyon, Ralph, Barrios, Moody and Bates18– Reference Xiao, Wang and Myatt21], near-backscattered imagers[ Reference Depierreux, Neuville, Baccou, Tassin, Casanova, Masson-Laborde, Borisenko, Orekhov, Colaitis, Debayle, Duchateau, Heron, Huller, Loiseau, Nicolaï, Pesme, Riconda, Tran, Bahr, Katz, Stoeckl, Seka, Tikhonchuk and Labaune22] and angular-resolved spectrometers[ Reference Zhao, Yuan, Zheng, Dong, Glize, Zhang, Zhang and Zhang23] can provide useful information. However, most of those diagnostic systems sample scattered lights within restricted orientations in the entire target chamber. To assess global energy losses and absorption uniformity, measurements are required to collect lights from the target across a significant portion of the space in the chamber. Conventional diagnostic methods, such as box calorimeters[ Reference Gunn and Rupert24, Reference Seka, Craxton, Delettrez, Goldman, Keck, McCrory, Shvarts, Soures and Boni25] and Ulbricht spheres[ Reference Godwin, Sachsenmaier and Sigel26], are capable of collecting large fractions of scattered lights, but are not suitable for integrated ICF experiment campaigns alongside various other diagnostics. Furthermore, since the scattered lights spread over a wide spectrum, full-spectral diagnostics are required for measuring the total energy losses from all types of LPIs. In addition, the absorbed energy could be diverted to other components in the coronal plasma, such as suprathermal electrons, instead of being coupled to implosions. Simultaneous measurements of the re-scattering on TPD plasma waves also support suprathermal electron diagnosis[ Reference Christopherson, Betti, Forrest, Howard, Theobald, Delettrez, Rosenberg, Solodov, Stoeckl, Patel, Gopalaswamy, Cao, Peebles, Edgell, Seka, Epstein, Wei, Johnson, Simpson, Regan and Campbell9]. Thus, it is essential to develop new diagnostic methods for detailed and accurate studies on laser absorption and full-spectral LPIs, which have a marked impact on direct-drive implosions.
In this work, a global and full-spectral scattered-light diagnostic system has been developed. It combines angular and spectral resolving capabilities to measure global distributions of optical emission spectra, providing insights into various processes of laser–plasma interactions through a compact system. It has been successfully implemented in the Shenguang-II Upgrade (SG-II UP)[ Reference Danson, Haefner, Bromage, Butcher, Chanteloup, Chowdhury, Galvanauskas, Gizzi, Hein, Hillier, Hopps, Kato, Khazanov, Kodama, Korn, Li, Li, Limpert, Ma, Nam, Neely, Papadopoulos, Penman, Qian, Rocca, Shaykin, Siders, Spindloe, Szatmári, Trines, Zhu, Zhu and Zuegel27, Reference Zhu, Zhu, Li, Zhu, Ma, Lu, Fan, Liu, Zhou, Xu, Zhang, Xie, Yang, Wang, Ouyang, Wang, Li, Yang, Fan, Sun, Liu, Liu, Zhang, Tao, Sun, Zhu, Wang, Jiao, Ren, Liu, Jiao, Huang and Lin28] laser facility. The globally spatial measurements have revealed laser absorption asymmetry. Meanwhile, the full-spectral characterizations have shown various LPIs, dominated by SRS, in the configuration of direct-drive conical implosions. From the integrated scattered energy, the total laser absorption efficiency has been assessed.
2 Principle and design
The 60-channel optical spectroscopy system has been designed to align with the configuration of the laser beams and target chamber in the SG-II UP facility. As shown in Figure 1(a), four nanosecond laser beams, denoted as #1, #3, #5 and #7 (with only three shown for clarity), are focused axisymmetrically at the same polar angle of 50° in the sphere, converging toward the target chamber center from the top. In addition, a picosecond laser, Beam #9, propagates in the equatorial plane and is focused at the center. There are 60 reflective collectors mounted on the inner wall above the equatorial plane, covering one-quarter of the sphere, among Beams #1, #3 and #7. The polarization angles of Beams #1 and #7 are 23° clockwise from the
![]() $\mathrm{p}$
-polarization, while those of Beams #3 and #5 are 7.5° counterclockwise. Since the polarization angles of the four beams are rotationally symmetrical, measurements covering a quarter of the spherical space can reveal the distribution in the 2
$\mathrm{p}$
-polarization, while those of Beams #3 and #5 are 7.5° counterclockwise. Since the polarization angles of the four beams are rotationally symmetrical, measurements covering a quarter of the spherical space can reveal the distribution in the 2
![]() $\pi$
solid angle. Each collector is equipped with a 90° ultraviolet (UV)-enhanced aluminum mirror that reflects light from the center to the input end of a fiber with a 192-μm-diameter core. The 60 fibers are bundled together at a flange, and these components are permanently installed at the SG-II UP facility.
$\pi$
solid angle. Each collector is equipped with a 90° ultraviolet (UV)-enhanced aluminum mirror that reflects light from the center to the input end of a fiber with a 192-μm-diameter core. The 60 fibers are bundled together at a flange, and these components are permanently installed at the SG-II UP facility.

Figure 1 Schematic diagram of the 60-channel optical spectrometer. Sixty reflective collectors are set on the inner side of the chamber wall, as shown in (a), collecting the lights emitted from the laser–target interactions. The angles of the laser beams are in the format of (
![]() $\theta$
,
$\theta$
,
![]() $\phi$
), where the polar angle is indicated as
$\phi$
), where the polar angle is indicated as
![]() $\theta$
and the azimuthal angle as
$\theta$
and the azimuthal angle as
![]() $\phi$
. The polarization angle from
$\phi$
. The polarization angle from
![]() $\mathrm{p}$
-polarization of Beams #1 and #7 is 23° clockwise, and that of Beams #3 and #5 is 7.5° anti-clockwise. The collectors reflect the lights to a fiber bundle, which is extended for 20 m outside the chamber to a spectrometer, as shown in (b), and the spectra are recorded by a CCD camera.
$\mathrm{p}$
-polarization of Beams #1 and #7 is 23° clockwise, and that of Beams #3 and #5 is 7.5° anti-clockwise. The collectors reflect the lights to a fiber bundle, which is extended for 20 m outside the chamber to a spectrometer, as shown in (b), and the spectra are recorded by a CCD camera.
The fiber bundle extends 20 m outside the vacuum chamber to protect electronic devices from radiations induced by high-power lasers. It is then coupled through a linear fiber array (see Figure 1(b)) to the 200-μm slit of the IsoPlane 160 imaging spectrometer, which has a focal length of 203 mm. The spectrometer is equipped with a triple turret that allows for the selection of gratings based on different experimental requirements. In one of our regular operating modes, with a 150-G/mm ruled grating, optical spectra in the 300–800 nm range can be recorded by a 13.3 mm × 13.3 mm area charge-coupled device (CCD) camera, achieving a spectral resolution of 6.3 nm. To obtain wider spectral ranges and higher resolution, two additional gratings with 50- and 1200-G/mm ruled lines can also be employed, with the main parameters shown in Table 1. The spectrometer slits are set to a width of 200 μm to ensure the detection of relatively weak light signals from the experiments. A fine spectral resolution of 0.3 nm has been calibrated using a 20-μm slit and a 1200-G/mm grating.
Table 1 List of the spectral ranges and resolution with a 200-μm slit using different ruled gratings.

3 Calibration and analysis
Since the diagnostic system measures a wide spectrum from UV to near-infrared, the calibration of the spectral response covered the range from 340 to 750 nm. Two light-emitting diode (LED) sources with known power and spectrum characteristics were selected: a continuum white LED emitting lights with wavelengths from 450 to 750 nm and a deep UV LED near 340 nm. The LED chips were set at the target chamber center respectively. Using the 150-G/mm grating in the spectrometer, the CCD recorded spectra of the LED lights collected by the fibers at different orientations. For the white LED, the CCD chip was filtered with a laminated neutral density film with 0.01
![]() $\%$
transmission for 400–700 nm, and the exposure time was 1000 s. For the UV LED, no filter was used in the spectrometer system considering the lower CCD quantum efficiency in the UV range, and the exposure time was 1 s. The signal of UV and white LED lights on the CCD is shown in Figure 2, where the horizontal axis represents light wavelengths and the vertical axis corresponds to different orientations of the fiber channels, with 15 pixels (full width at 1/e of maximum intensity) for each channel. Due to optical damage or target splashing after laser shots and obstruction by other diagnostics, 43 of the 60 channels were able to collect lights during this experimental campaign.
$\%$
transmission for 400–700 nm, and the exposure time was 1000 s. For the UV LED, no filter was used in the spectrometer system considering the lower CCD quantum efficiency in the UV range, and the exposure time was 1 s. The signal of UV and white LED lights on the CCD is shown in Figure 2, where the horizontal axis represents light wavelengths and the vertical axis corresponds to different orientations of the fiber channels, with 15 pixels (full width at 1/e of maximum intensity) for each channel. Due to optical damage or target splashing after laser shots and obstruction by other diagnostics, 43 of the 60 channels were able to collect lights during this experimental campaign.
The light power at the input end of the reflecting mirror was measured using a power meter. The products of the power and the exposure time provided the energy input to each channel, establishing a response relationship with the recorded spectral intensity on the CCD. The spectral response of the system is influenced by various factors, including the reflectivity of the aluminum mirror, the transmission attenuation of the fibers, the grating efficiency and the CCD quantum efficiency. Each component’s attenuation acts as a constant neutral density. Based on the calibrated LED spectra, the response of the entire optical system,
![]() $R$
(
$R$
(
![]() $i$
,
$i$
,
![]() ${\lambda}_j$
), for a specific wavelength
${\lambda}_j$
), for a specific wavelength
![]() ${\lambda}_j$
(with
${\lambda}_j$
(with
![]() $j$
denoting the CCD pixel on the spectral dimension) in channel
$j$
denoting the CCD pixel on the spectral dimension) in channel
![]() $i$
, can be derived using the following procedure.
$i$
, can be derived using the following procedure.
For channel
![]() $i$
set at a specific orientation, the input power measured in front of the collector is
$i$
set at a specific orientation, the input power measured in front of the collector is
![]() ${P}_{\mathrm{src}}$
(
${P}_{\mathrm{src}}$
(
![]() $i$
). Given the known spectrum
$i$
). Given the known spectrum
![]() $\eta$
(
$\eta$
(
![]() $\lambda$
) of the LED emission source, the power at wavelength
$\lambda$
) of the LED emission source, the power at wavelength
![]() ${\lambda}_j$
per unit wavelength d
${\lambda}_j$
per unit wavelength d
![]() $\lambda$
is calculated as
$\lambda$
is calculated as
 ${P}_{\mathrm{src}}\left(i,{\lambda}_j\right)={P}_{\mathrm{src}}(i)\frac{\int_{\lambda_j}^{\lambda_j+\mathrm{d}\lambda}\eta \mathrm{d}\lambda }{\int_{-\infty}^{\infty}\eta \mathrm{d}\lambda }$
, which results in an intensity on the detector
${P}_{\mathrm{src}}\left(i,{\lambda}_j\right)={P}_{\mathrm{src}}(i)\frac{\int_{\lambda_j}^{\lambda_j+\mathrm{d}\lambda}\eta \mathrm{d}\lambda }{\int_{-\infty}^{\infty}\eta \mathrm{d}\lambda }$
, which results in an intensity on the detector
![]() ${I}_{\mathrm{src}}\left(i,{\lambda}_j\right)$
. Thus, the response (intensity per unit input energy) of the system in channel
${I}_{\mathrm{src}}\left(i,{\lambda}_j\right)$
. Thus, the response (intensity per unit input energy) of the system in channel
![]() $i$
and at wavelength
$i$
and at wavelength
![]() ${\lambda}_j$
is given by
${\lambda}_j$
is given by
![]() $R\left(i,{\lambda}_j\right)={I}_{\mathrm{src}}\left(i,{\lambda}_j\right)/\left({P}_{\mathrm{src}}\left(i,{\lambda}_j\right){\tau}_{\mathrm{exp}}\right)$
, where
$R\left(i,{\lambda}_j\right)={I}_{\mathrm{src}}\left(i,{\lambda}_j\right)/\left({P}_{\mathrm{src}}\left(i,{\lambda}_j\right){\tau}_{\mathrm{exp}}\right)$
, where
![]() ${\tau}_{\mathrm{exp}}$
is the CCD exposure time. When the experimental signal
${\tau}_{\mathrm{exp}}$
is the CCD exposure time. When the experimental signal
![]() ${I}_{\mathrm{sig}}\left(i,{\lambda}_j\right)$
is recorded, the energy of the signal in front of the fiber collectors can be calculated as
${I}_{\mathrm{sig}}\left(i,{\lambda}_j\right)$
is recorded, the energy of the signal in front of the fiber collectors can be calculated as
![]() $E\left(i,{\lambda}_j\right)={I}_{\mathrm{sig}}\left(i,{\lambda}_j\right)/R\left(i,{\lambda}_j\right)=\frac{I_{\mathrm{sig}}\left(i,{\lambda}_j\right)}{I_{\mathrm{src}}\left(i,{\lambda}_j\right)}{P}_{\mathrm{src}}\left(i,{\lambda}_j\right){\tau}_{\mathrm{exp}}$
.
$E\left(i,{\lambda}_j\right)={I}_{\mathrm{sig}}\left(i,{\lambda}_j\right)/R\left(i,{\lambda}_j\right)=\frac{I_{\mathrm{sig}}\left(i,{\lambda}_j\right)}{I_{\mathrm{src}}\left(i,{\lambda}_j\right)}{P}_{\mathrm{src}}\left(i,{\lambda}_j\right){\tau}_{\mathrm{exp}}$
.

Figure 2 Mosaic image of the UV and white LED spectra recorded by the spectrometer with the 150-G/mm grating. Here the white LED light was recorded with an OD4 filter and 1000-s exposure. The UV one was recorded with 1-s exposure and the intensity was artificially reduced by a factor of 10 for better visibility.
4 Experimental results
The spectrometer system has been employed to measure the laser absorption in the conical compression stage of the double-cone ignition scheme[
Reference Zhang, Wang, Yang, Wu, Ma, Jiao, Zhang, Wu, Yuan, Li and Zhu29] at the SG-II UP facility. In this setup, the four laser beams overlapped on a C16H14Cl2 (CHCl) spherical shell within a gold cone (shell-in-cone target), and drove a conical implosion of the shell, as shown in Figure 3(a). Each beam delivered 1500 J of energy at a UV wavelength of 351 nm (tripled frequency
![]() $\omega =3{\omega}_0$
), and was focused onto the shell through a 700-μm diameter spot determined by a
$\omega =3{\omega}_0$
), and was focused onto the shell through a 700-μm diameter spot determined by a
![]() $\Phi$
700 continuous phase plate. The temporally shaped laser pulse is shown in Figure 3(b). The resulting intensity of the four overlapped beams reached a maximum of 5.7×1014 W/cm2. The CHCl shell had a thickness of 50 μm and an inner radius of 500 μm, with the shell cap having a full opening angle of 100°. The orientations of the laser irradiation and the fiber collectors are shown in the angular coordinates in Figure 3(c), with the 90° polar angle defined as the equatorial plane and the 0° azimuthal angle as the incidence of Beam #3.
$\Phi$
700 continuous phase plate. The temporally shaped laser pulse is shown in Figure 3(b). The resulting intensity of the four overlapped beams reached a maximum of 5.7×1014 W/cm2. The CHCl shell had a thickness of 50 μm and an inner radius of 500 μm, with the shell cap having a full opening angle of 100°. The orientations of the laser irradiation and the fiber collectors are shown in the angular coordinates in Figure 3(c), with the 90° polar angle defined as the equatorial plane and the 0° azimuthal angle as the incidence of Beam #3.

Figure 3 (a) Schematic diagram of the conical irradiation. The spherical CHCl shell is initially embedded in the gold cone, and four laser beams overlap at the shell surface through 700-μm continuous phase plates. (b) Laser temporal profile on the target. (c) The coordinates of the collectors in the 2D angular map, with Beams #1, #3 and #7 incident angles.
The spatial growth of LPIs is influenced by the laser polarization directions. The polarization angles of Beams #1 and #7 are identical, as are those of Beams #3 and #5. Consequently, measurements in one-quarter of the sphere can reveal the light distribution in the entire hemisphere. The total scattered energy proportion
![]() ${f}_{\mathrm{scatt}}$
can be calculated from the spectral and angular integration, allowing the laser absorption efficiency
${f}_{\mathrm{scatt}}$
can be calculated from the spectral and angular integration, allowing the laser absorption efficiency
![]() ${f}_{\mathrm{abs}}$
to be deduced using the following equations:
${f}_{\mathrm{abs}}$
to be deduced using the following equations:
 $$\begin{align*}{f}_{\mathrm{scatt}}=2{\int}_0^{\pi /2}{\int}_0^{\pi}\frac{\mathrm{d}{E}_{\mathrm{scatt}}}{\mathrm{d}\Omega}\left(\theta, \phi \right)\sin \theta \mathrm{d}\theta \mathrm{d}\phi /{E}_{\mathrm{las}},\end{align*}$$
$$\begin{align*}{f}_{\mathrm{scatt}}=2{\int}_0^{\pi /2}{\int}_0^{\pi}\frac{\mathrm{d}{E}_{\mathrm{scatt}}}{\mathrm{d}\Omega}\left(\theta, \phi \right)\sin \theta \mathrm{d}\theta \mathrm{d}\phi /{E}_{\mathrm{las}},\end{align*}$$
Here
![]() $\theta$
and
$\theta$
and
![]() $\phi$
represent the polar and azimuthal angles in the sphere, respectively, while
$\phi$
represent the polar and azimuthal angles in the sphere, respectively, while
![]() ${E}_{\mathrm{las}}$
is the incident laser energy on target. Linear interpolation of intensity is used in the angular integration for the directions between adjacent collectors. Furthermore, the spectrum of scattered light contains valuable information on various laser–plasma interaction processes and parametric instabilities.
${E}_{\mathrm{las}}$
is the incident laser energy on target. Linear interpolation of intensity is used in the angular integration for the directions between adjacent collectors. Furthermore, the spectrum of scattered light contains valuable information on various laser–plasma interaction processes and parametric instabilities.
4.1 Laser–plasma instabilities
Figure 4(a) shows a typical result of global scattered light recorded by the spectrometer system using the 150-G/mm grating and the ND4 filter. According to the frequency matching conditions between the parent laser wave and the daughter waves, the spectra of the scattered light can characterize different LPI processes. The lights around 351 nm consist of the direct reflection of the incident laser, SBS and CBET. The contributions from the three main parts are currently indistinguishable, but these would be resolved by using gratings with denser lines for better spectral resolution to observe wavelength shifts. The lights around 527 nm, primarily from the 2
![]() ${\omega}_0$
remnant of the laser, are randomly reflected from the chamber and excluded from the scattered energy calculation. The continuum spectrum from 500 to 650 nm is from SRS, which occurs in sub-critical plasma with a density lower than the quarter critical density, and dominates the side scattering in this configuration[
Reference Glize, Zhao, Zhang, Lian, Tan, Wu, Xiao, Yan, Zhang, Yuan and Zhang20]. TPD re-scattering in the branch around
${\omega}_0$
remnant of the laser, are randomly reflected from the chamber and excluded from the scattered energy calculation. The continuum spectrum from 500 to 650 nm is from SRS, which occurs in sub-critical plasma with a density lower than the quarter critical density, and dominates the side scattering in this configuration[
Reference Glize, Zhao, Zhang, Lian, Tan, Wu, Xiao, Yan, Zhang, Yuan and Zhang20]. TPD re-scattering in the branch around
![]() $\omega$
/2 (680–720 nm) has also been observed. The red-shifted peak in the
$\omega$
/2 (680–720 nm) has also been observed. The red-shifted peak in the
![]() $\omega$
/2 spectra at a polar angle around 8° indicates electron temperature at quarter critical density of 1.6 ± 0.4 keV. In addition, the 3
$\omega$
/2 spectra at a polar angle around 8° indicates electron temperature at quarter critical density of 1.6 ± 0.4 keV. In addition, the 3
![]() $\omega$
/2 spectra (230–238 nm) from TPD re-scattering are generated by Thomson up-scattering of the incident laser, which requires a broad spectrum of plasma waves[
Reference Seka, Myatt, Short, Froula, Katz, Goncharov and Igumenshchev15]. Since the 3
$\omega$
/2 spectra (230–238 nm) from TPD re-scattering are generated by Thomson up-scattering of the incident laser, which requires a broad spectrum of plasma waves[
Reference Seka, Myatt, Short, Froula, Katz, Goncharov and Igumenshchev15]. Since the 3
![]() $\omega$
/2 spectra have been observed to occupy less than 0.3
$\omega$
/2 spectra have been observed to occupy less than 0.3
![]() $\%$
of the total scattered energy (equivalent to 10−4 of the laser energy) in a prior experiment with a similar configuration, the spectrometer system has not been used with the 50-G/mm grating for simultaneous measurements of the spectra at 3
$\%$
of the total scattered energy (equivalent to 10−4 of the laser energy) in a prior experiment with a similar configuration, the spectrometer system has not been used with the 50-G/mm grating for simultaneous measurements of the spectra at 3
![]() $\omega$
/2.
$\omega$
/2.

Figure 4 (a) Raw image for the multi-channel spectra of the scattered lights from the laser-driven shell-in-cone target implosion. Here the longitudinal axis represents collectors at different orientations, and the wavelength in spectra indicates different processes of LPIs (the spectral response needs to be taken into account for absolute energy calculation). The corresponding angular distributions of the 351-nm lights, SRS and
![]() $\omega$
/2 re-scattering TPD are shown in (b), (c) and (d), using linear interpolation for the directions in between two adjacent collectors. The incident angles for the laser beams are shown in the angular distribution maps.
$\omega$
/2 re-scattering TPD are shown in (b), (c) and (d), using linear interpolation for the directions in between two adjacent collectors. The incident angles for the laser beams are shown in the angular distribution maps.
Typical results for the two-dimensional (2D) angular distributions of energy in the three main spectral components are presented in Figures 4(b)–4(d), corresponding to 351-nm scattering, broadband SRS (around 500–650 nm) and the
![]() $\omega$
/2 branch of TPD (680–720 nm), respectively. The nonuniformity and asymmetry in these distributions could be attributed to beam energy and pointing imbalances, as well as laser polarization effects on LPIs. The 351-nm lights were primarily distributed in the polar directions around the laser incidence (40°–70°), with very weak emissions in larger or smaller angles, covering a broad span in azimuthal directions between every two beams (see Figure 4(b)). Among the shots in this experiment, the integrated energy of the 351-nm lights is
$\omega$
/2 branch of TPD (680–720 nm), respectively. The nonuniformity and asymmetry in these distributions could be attributed to beam energy and pointing imbalances, as well as laser polarization effects on LPIs. The 351-nm lights were primarily distributed in the polar directions around the laser incidence (40°–70°), with very weak emissions in larger or smaller angles, covering a broad span in azimuthal directions between every two beams (see Figure 4(b)). Among the shots in this experiment, the integrated energy of the 351-nm lights is
![]() ${0.9}_{-0.3}^{+0.8}\%$
(in the format
${0.9}_{-0.3}^{+0.8}\%$
(in the format
![]() $\mathrm{average}_{\mathrm{lower\kern0.17em limit}}^{\mathrm{upper\kern0.17em limit}}$
) of the laser energy. For the broadband SRS, the emissions are close to the laser incidence (Figure 4(c)), indicating they are likely driven by single-beam-induced scattering. The energy conversion to SRS is
$\mathrm{average}_{\mathrm{lower\kern0.17em limit}}^{\mathrm{upper\kern0.17em limit}}$
) of the laser energy. For the broadband SRS, the emissions are close to the laser incidence (Figure 4(c)), indicating they are likely driven by single-beam-induced scattering. The energy conversion to SRS is
![]() ${2.9}_{-0.4}^{+2.6}\%$
of the laser energy. The TPD emissions near
${2.9}_{-0.4}^{+2.6}\%$
of the laser energy. The TPD emissions near
![]() $\omega$
/2 are observed at polar angles less than 50° (Figure 4(d)), which can be explained by the light refraction due to the density gradient[
Reference Seka, Myatt, Short, Froula, Katz, Goncharov and Igumenshchev15]. The total energy of the
$\omega$
/2 are observed at polar angles less than 50° (Figure 4(d)), which can be explained by the light refraction due to the density gradient[
Reference Seka, Myatt, Short, Froula, Katz, Goncharov and Igumenshchev15]. The total energy of the
![]() $\omega$
/2 emissions is
$\omega$
/2 emissions is
![]() ${0.3}_{-0.1}^{+0.4}\%$
of the laser energy.
${0.3}_{-0.1}^{+0.4}\%$
of the laser energy.
4.2 Laser absorption
The three main spectral components provide an overall scattered energy of
![]() ${4.1}_{-0.5}^{+2.8}\%$
of the laser energy, with errors summing those of the three main spectral components in quadrature. An FABS system was installed on Beam #7 and absolutely calibrated. The calorimeters of the FABS were filtered to measure in the 275–375 nm range and a broad spectrum beyond 400 nm, indicating on average 1.2% and 0.1% of the laser energy in 351-nm lights and SRS, respectively, amounting to a total of 1.3% in backscattering. The results from the spectrometer system and FABS give an averaged global scattered energy of 5.4%, which suggests approximately 94.6% laser absorption in the conical implosion driven by the four overlapped laser beams with a peak intensity of 5.7×1014 W/cm2.
${4.1}_{-0.5}^{+2.8}\%$
of the laser energy, with errors summing those of the three main spectral components in quadrature. An FABS system was installed on Beam #7 and absolutely calibrated. The calorimeters of the FABS were filtered to measure in the 275–375 nm range and a broad spectrum beyond 400 nm, indicating on average 1.2% and 0.1% of the laser energy in 351-nm lights and SRS, respectively, amounting to a total of 1.3% in backscattering. The results from the spectrometer system and FABS give an averaged global scattered energy of 5.4%, which suggests approximately 94.6% laser absorption in the conical implosion driven by the four overlapped laser beams with a peak intensity of 5.7×1014 W/cm2.
Further improvement of the spectrometer system is currently underway, including the integration of an intensified CCD with a fast time gate to record the history of laser energy absorption. In addition to measuring laser absorption in ICF experiments, work is in progress using this spectrometer to diagnose relativistic laser–plasma interactions. With the high-power picosecond Beam #9 of SG-II UP facility, optical spectra of laser light scattered from the target surface (such as 2
![]() ${\omega}_0$
and 3
${\omega}_0$
and 3
![]() ${\omega}_0$
/2 harmonics) can provide valuable insights into fast electron generation and transportation.
${\omega}_0$
/2 harmonics) can provide valuable insights into fast electron generation and transportation.
5 Conclusions
A new diagnostic method was designed and developed for global and full-optical measurements on scattered lights, with a 60-channel fiber bundle and a spectrometer, offering resolution for both spectral and angular distributions. It covers a steradian of
![]() $\pi$
in a solid angle and spans a spectral range from UV to near-infrared. The spectrometer system has been tested experimentally for diagnosing laser absorption and LPIs driven by the nanosecond lasers of the SG-II UP facility. Following the absolute calibration using LED sources and according to an axisymmetric configuration of the laser irradiation, the integrated energy of the scattered lights has provided the global laser absorption rate. Besides, the spectra measured with multiple channels also reveal LPI processes primarily driven by SRS in the conical irradiation configuration. This diagnostic system can provide invaluable data, which enables the calibration of novel models for LPI simulations. It will allow predictions for implosion experiments and improve our understanding and mitigation of LPIs.
$\pi$
in a solid angle and spans a spectral range from UV to near-infrared. The spectrometer system has been tested experimentally for diagnosing laser absorption and LPIs driven by the nanosecond lasers of the SG-II UP facility. Following the absolute calibration using LED sources and according to an axisymmetric configuration of the laser irradiation, the integrated energy of the scattered lights has provided the global laser absorption rate. Besides, the spectra measured with multiple channels also reveal LPI processes primarily driven by SRS in the conical irradiation configuration. This diagnostic system can provide invaluable data, which enables the calibration of novel models for LPI simulations. It will allow predictions for implosion experiments and improve our understanding and mitigation of LPIs.
Acknowledgements
This work was supported by the Strategic Priority Research Program of the Chinese Academy of Sciences (Nos. XDA25010100, XDA25010300 and XDA25030100), in part by the National Natural Science Foundation of China (No. 12105359) and the Chinese Academy of Sciences Youth Interdisciplinary Team (No. JCTD-2022-05). The authors thank the staff members of the SG-II Upgrade facility (https://cstr.cn/31126.02.SGII.UP.HPLF) at the Shenguang-II High Power Laser Facility in Shanghai (https://cstr.cn/31126.02.SGII), for providing technical support and assistance in data collection and analysis.