1 Introduction
Interest in the experimental study of warm dense matter (WDM) especially in relation to planetary interiors and high pressure states has been around since the invention of the diamond anvil cell (DAC) that could be used to reach high pressures and temperatures[Reference Boehler1]. The field experienced an accelerated development over the past two decades with the commissioning of many new laser and accelerator facilities and specific diagnostic techniques capable of generating and studying this challenging regime[Reference Ganziani2]. WDM is generally considered to be an array of states of matter, primarily strongly coupled plasmas, at moderately high temperatures ranging from 0.1 to 100 eV, and solid densities. In many cases we also talk about high pressure systems reaching above 1 Mbar. WDM can exhibit properties of both ideal plasmas and correlated systems similar to those found in condensed matter while ranging over a wide span of thermodynamic conditions. Ions in this regime of matter are strongly coupled and fluid-like with no long-range order, whereas electrons are fully or partially degenerate. Therefore, quantum effects, normally neglected in ideal plasmas, become important in WDM. For these reasons WDM is also a challenging regime of matter to describe theoretically, as many standard approximations are not valid. WDM is thus very hard to define and is poorly understood by current theory. Figure 1 shows a density–temperature phase diagram ranging from solid-state physics to extreme states of matter over a variety of plasma conditions found in the laboratory or in astrophysical objects.
A convenient way to place WDM on the phase diagram is using the definition of the coupling parameter
![]() $\unicode[STIX]{x1D6E4}=Z^{2}e^{2}/4\unicode[STIX]{x1D70B}\unicode[STIX]{x1D716}_{0}dk_{B}T$
, which is the ratio of the Coulomb and kinetic energies. Here
$\unicode[STIX]{x1D6E4}=Z^{2}e^{2}/4\unicode[STIX]{x1D70B}\unicode[STIX]{x1D716}_{0}dk_{B}T$
, which is the ratio of the Coulomb and kinetic energies. Here
![]() $Z$
,
$Z$
,
![]() $e$
,
$e$
,
![]() $k_{B}$
and
$k_{B}$
and
![]() $T$
correspond to the ionization state, electron charge, Boltzmann constant and temperature. At the extreme end of the scale at high values of
$T$
correspond to the ionization state, electron charge, Boltzmann constant and temperature. At the extreme end of the scale at high values of
![]() $\unicode[STIX]{x1D6E4}$
we encounter strongly coupled condensed matter, i.e., room temperature solids with tightly bound ions often forming crystalline lattices. Weakly coupled ideal plasma, where Coulomb interactions between ions are weak, appears at the top of the phase diagram with
$\unicode[STIX]{x1D6E4}$
we encounter strongly coupled condensed matter, i.e., room temperature solids with tightly bound ions often forming crystalline lattices. Weakly coupled ideal plasma, where Coulomb interactions between ions are weak, appears at the top of the phase diagram with
![]() $\unicode[STIX]{x1D6E4}$
less than unity. Due to high densities, the electrons in WDM experience Pauli blocking as many are pushed into the Fermi sea. We define the degeneracy parameter as a ratio of thermal and Fermi energies
$\unicode[STIX]{x1D6E4}$
less than unity. Due to high densities, the electrons in WDM experience Pauli blocking as many are pushed into the Fermi sea. We define the degeneracy parameter as a ratio of thermal and Fermi energies
![]() $\unicode[STIX]{x1D6E9}=T_{e}/T_{F}$
. In WDM these values are usually close to 1 or
$\unicode[STIX]{x1D6E9}=T_{e}/T_{F}$
. In WDM these values are usually close to 1 or
![]() ${<}1$
. Partial ionization of WDM influences the microscopic arrangement of ions due to the short-range repulsion between bound electrons[Reference Ganziani2]. The level of electron degeneracy and the microscopic structure of WDM have a significant effect on thermodynamic and atomic properties of WDM including electron–ion equilibration time or plasma resistivity, compressibility and internal energy.
${<}1$
. Partial ionization of WDM influences the microscopic arrangement of ions due to the short-range repulsion between bound electrons[Reference Ganziani2]. The level of electron degeneracy and the microscopic structure of WDM have a significant effect on thermodynamic and atomic properties of WDM including electron–ion equilibration time or plasma resistivity, compressibility and internal energy.
WDM is common in astrophysical objects, such as interiors of Jovian planets (also referred to as gas giants, e.g., Jupiter or Saturn), ice giants (e.g., Neptune), brown dwarfs, white dwarfs, low-mass stars, or crusts of old stars, all of which are predominantly composed of light elements such as hydrogen, helium and carbon[Reference Lebedev3, Reference Guillot4]. WDM can also be found in terrestrial planets with hot metallic cores, and thus much of the research interest is directed towards high pressure phases of iron[Reference Nguyen and Holmes5]. With the recent discovery of exoplanets, the range of conditions has expanded to more extreme pressures, temperatures and other materials. Studying phase changes, metallization and dissociation with increasing pressures and temperatures to the WDM regime is the key to modelling the structure and magnetic fields of these objects. Most of the initial experimental research in high pressure plasma phases was linked to geophysics and planetary science with a special focus on giant gaseous planets and small rocky planets using static compression with DAC[Reference Boehler1]. Dense plasma states can also be generated in astrophysical shocks such as supernova explosions[Reference Lebedev3].

Figure 1. Phase diagram for the WDM regime. WDM lies between condensed matter, hot dense matter and ideal plasma (low densities), and overlaps the planar laser-generated shocks in matter as well as the astrophysical conditions.
![]() $\unicode[STIX]{x1D6E4}$
is the coupling parameter (ratio of Coulomb and thermal energy) so the
$\unicode[STIX]{x1D6E4}$
is the coupling parameter (ratio of Coulomb and thermal energy) so the
![]() $\unicode[STIX]{x1D6E4}=1$
line separates the strongly and weakly coupled regimes, and
$\unicode[STIX]{x1D6E4}=1$
line separates the strongly and weakly coupled regimes, and
![]() $\unicode[STIX]{x1D707}$
stands for the chemical potential where the
$\unicode[STIX]{x1D707}$
stands for the chemical potential where the
![]() $\unicode[STIX]{x1D707}=0$
line signifies the area where the Fermi energy equals
$\unicode[STIX]{x1D707}=0$
line signifies the area where the Fermi energy equals
![]() $k_{B}T$
, below which we get Fermi degenerate matter.
$k_{B}T$
, below which we get Fermi degenerate matter.
WDM is also created when laser radiation heats up solid targets in deuterium–tritium-fuel pellets during inertial confinement fusion (ICF) implosions[Reference Nuckolls6]. Thus the first interest of the high power laser community in the study of WDM equation of state (EOS) was triggered by the initial research carried out on the ICF technology, since it soon became apparent that the EOS of WDM would play an important role in the efficiency of implosion of the DT ice pellets[Reference Nuckolls6]. But it was not until mid-1990s, when the large scale laser and z-pinch facilities like the OMEGA laser or the Z-machine were built, that the field truly boomed thanks to novel technology capable of generating WDM. This interest quickly expanded to other fields such as materials under extreme conditions, laboratory astrophysics, shock physics, explosives, laser processes, solid–liquid–plasma phase transitions as well as industrial applications[Reference Koenig7]. Due to the challenging combination of properties, i.e., high density and pressure, but relatively low-to-moderate temperature, it took many years to develop reliable diagnostic techniques to probe WDM. With the development of novel facilities such as short-pulse optical lasers and X-ray free electron lasers (FELs) capable of delivering pulses with femtosecond duration and high repetition rates, the field is currently undergoing another major transition. With these new generation radiation sources, experiments can achieve a wider range of WDM conditions and probing of nonequilibrium states.
The main focus of this paper is experimental measurements of structure and thermodynamic state of WDM relevant to planetary science and geophysics primarily from the point of view of the laser community. However, related topics associated with dynamic compression experiments at z-pinch facilities are also provided. Even though static compression techniques carried out with DAC usually access a different sort of conditions, this work is complementary to the WDM research done at laser facilities. Since these methods have been recently combined in order to achieve even more extreme pressures of WDM states by driving shock waves in pre-compressed samples, a quick outline of this field is also included as a reference to the laser community. The new methods of generating and probing WDM with novel short-pulse radiation sources are described in detail. Developments in the theoretical description of WDM with emphasis on EOS models, transport properties such as conductivity and their application for simulations of planetary structures and formation are also briefly reviewed at the end of this publication.
2 Planetary interiors
A detailed understanding of the EOS and related properties like compressibility of light elements like hydrogen, helium and carbon under extreme conditions is essential for the modelling of the evolution and inner structure of giant gaseous planets and brown dwarfs[Reference Guillot4, Reference Hubbard8–Reference Nettelmann10]. The current planetary models rely on incomplete information to interpret the gravitational moments, total mass and spectroscopic measurements from telescopes and probes sent to Jupiter and Saturn. The full description of the structure of these planets remains uncertain in the absence of accurate EOS information for the strongly coupled degenerate matter within[Reference Guillot11, Reference Remington, Drake and Ryutov12].
Molecular hydrogen at moderate temperatures (
![]() ${\lesssim}10^{5}$
K
${\lesssim}10^{5}$
K
![]() ${\sim}0.9$
eV) dissociates and eventually ionizes undergoing a phase transition to a metallic phase once the pressure increases beyond
${\sim}0.9$
eV) dissociates and eventually ionizes undergoing a phase transition to a metallic phase once the pressure increases beyond
![]() ${\sim}1$
Mbar creating an effective barrier between the He-rich molecular hydrogen layer in Jupiter and He-poor metallic hydrogen underneath[Reference Guillot4]. It is however not clear whether this transition is continuous or discontinuous, i.e., first-order plasma phase transition (PPT). The density-functional molecular dynamics (DFT-MD) simulations predict a continuous transition from the molecular to a dissociated regime in fluid hydrogen under the conditions of Jupiter’s interior[Reference Militzer9, Reference Vorberger13, Reference Vorberger14]. Other widely recognized models predict PPT[Reference Saumon, Chabrier and Horn15–Reference Morales17]. Early shock-compression experiments found no evidence of abrupt phase transition concluding that the dissociation of molecular fluid is likely to be continuous[Reference da Silva18–Reference Boriskov21]. Later experimental evidence however supports the existence of PPT in hydrogen and deuterium[Reference Fortov22, Reference Eremets and Troyan23]. The presence of PPT provides an effective entropy barrier within the planet’s interior that cannot be crossed by convection[Reference Stevenson and Salpeter24]. The PPT scenario therefore strongly supports the three-layer model as it predicts a sharp separation of the molecular and metallic regions[Reference Stevenson and Salpeter24].
${\sim}1$
Mbar creating an effective barrier between the He-rich molecular hydrogen layer in Jupiter and He-poor metallic hydrogen underneath[Reference Guillot4]. It is however not clear whether this transition is continuous or discontinuous, i.e., first-order plasma phase transition (PPT). The density-functional molecular dynamics (DFT-MD) simulations predict a continuous transition from the molecular to a dissociated regime in fluid hydrogen under the conditions of Jupiter’s interior[Reference Militzer9, Reference Vorberger13, Reference Vorberger14]. Other widely recognized models predict PPT[Reference Saumon, Chabrier and Horn15–Reference Morales17]. Early shock-compression experiments found no evidence of abrupt phase transition concluding that the dissociation of molecular fluid is likely to be continuous[Reference da Silva18–Reference Boriskov21]. Later experimental evidence however supports the existence of PPT in hydrogen and deuterium[Reference Fortov22, Reference Eremets and Troyan23]. The presence of PPT provides an effective entropy barrier within the planet’s interior that cannot be crossed by convection[Reference Stevenson and Salpeter24]. The PPT scenario therefore strongly supports the three-layer model as it predicts a sharp separation of the molecular and metallic regions[Reference Stevenson and Salpeter24].
Another important topic is the size and composition of the central core of giant gaseous planets. Many evolutionary models predict that gas giants formed from small rocky planetesimals, which acted as seeds for the planets to grow on top of[Reference Lissauer25]. Other theories assume that the core formed early in the centre of a very tenuous nonconvective protoplanetary clump[Reference Boss26]. The core composition cannot be derived from the gravitational moments measurements. In fact its mass heavily depends on the EOS; therefore, hydrogen EOS determines whether Jupiter has to have a rock core or not[Reference Drake27].
An interesting phenomenon predicted by theoretical models is phase separation of various materials and elements. A famous example is phase separation of H and He inside Jupiter. Since He requires larger pressure than H to become ionized there is a possibility of a separation between He-rich and He-poor mixtures within the deep interior of the gas giants[Reference Salpeter28]. Although there is no reliable EOS available for H/He, it is mostly agreed that this phase separation happens around the boundary of the metallic region[Reference Pfaffenzeller29–Reference Stevenson31]. Around this region He-rich droplets form within the metallic H fluid, grow rapidly and consequently fall towards the interior of the planet without being efficiently transported by convection[Reference Stevenson and Salpeter24]. This is also sometimes referred to as “helium rain,” which remains to be the only viable explanation for the low concentration of He in the atmospheres of the giant planets compared to the protostellar nebula from which the solar system formed[Reference Guillot11]. Apart from H and He, a great research interest is also focused on carbon and light carbohydrates which are abundant in icy giants, exoplanets or even white dwarfs[Reference Ross32–Reference Dufour34]. Specifically the predicted phase separation of H or simple carbohydrates and pure carbon under extreme pressures is of a great interest to planetary science, which has now been proven experimentally[Reference Ross32, Reference Kraus35].
High pressure water phases are abundant in icy moons and extrasolar planetary bodies and thus evaluation of extreme condition behaviour of impurity-laden ices is critical for modelling of these astrophysical bodies[Reference Gleason36]. In the case of icy giants like Uranus or Neptune, information about EOS and transport properties of water, methane, ammonia or CHNO mixtures at pressures exceeding 100 GPa is also very important for the understanding of their structures and dynamics[Reference Remington, Drake and Ryutov12]. Conductivity and high pressure behaviour of Fe are relevant to the study of terrestrial planets[Reference Nguyen and Holmes5]. Measurement of the melting temperature of Fe at very high pressures is crucial for deriving the temperature of the terrestrial planet cores. The knowledge of Fe EOS is thus a key to solving fundamental questions about Earth’s geodynamics, thermal evolution and heat budget. Much of WDM research looks at extreme states of composite materials, especially rock-forming minerals and compounds that make up mantles of terrestrial planets including complex silicates like (Mg, Fe)SiO
![]() $_{3}$
and (Mg, Fe)
$_{3}$
and (Mg, Fe)
![]() $_{2}$
SiO
$_{2}$
SiO
![]() $_{4}$
or magnesium oxide. With the discovery of exoplanets, especially large rocky planets called super-Earths, where pressures can exceed TPa levels, properties of these materials at even higher pressures than those found inside Earth gained a lot of interest in the research community.
$_{4}$
or magnesium oxide. With the discovery of exoplanets, especially large rocky planets called super-Earths, where pressures can exceed TPa levels, properties of these materials at even higher pressures than those found inside Earth gained a lot of interest in the research community.
For example, magnesium oxide is expected to change from a rocksalt crystal structure (B1) to a caesium chloride (B2) structure at pressures of about 400–600 GPa[Reference Oganov37, Reference Belonoshko38]. This phase transition in MgO under relevant WDM conditions has recently been confirmed experimentally[Reference McWilliams39, Reference Coppari40]. One of the mesmerizing questions in geophysics is related to the transformation pathway and pressure–temperature range of formation for diaplectic silica glass as a bulk glass or in amorphous lamellae as planar deformation features, which serve as the best-studied mineralogical shock barometer[Reference Sharp and DeCarli41]. Silicates have been extensively studied in both the static and dynamic compression experiments giving conflicting answers. While static compression results on quartz show evidence of on-compression pressure-induced amorphization above
![]() ${\sim}30$
GPa[Reference Hemley42], dynamic compression experiments in the so-called “mixed phase region” (
${\sim}30$
GPa[Reference Hemley42], dynamic compression experiments in the so-called “mixed phase region” (
![]() ${>}20$
GPa) of the principal Hugoniot are interpreted as a transformation to stishovite, which then reverts back to glass[Reference Luo43]. This interpretation is questioned due to the reconstructive nature of the quartz-to-stishovite transition and the expected sluggish kinetics[Reference Langenhorst44]. Novel experimental study of the pressure–temperature–time path and time-resolved in situ diffraction measurements of experimentally shocked samples now provide a better understanding of the formation of diaplectic glass and its significance for naturally shocked samples[Reference Gleason45].
${>}20$
GPa) of the principal Hugoniot are interpreted as a transformation to stishovite, which then reverts back to glass[Reference Luo43]. This interpretation is questioned due to the reconstructive nature of the quartz-to-stishovite transition and the expected sluggish kinetics[Reference Langenhorst44]. Novel experimental study of the pressure–temperature–time path and time-resolved in situ diffraction measurements of experimentally shocked samples now provide a better understanding of the formation of diaplectic glass and its significance for naturally shocked samples[Reference Gleason45].
WDM is also generated in dynamic processes such as collisions between celestial bodies, e.g., asteroid impacts on Earth, where rocks are suddenly subjected to very high pressures and temperatures resulting in so-called shock metamorphism[Reference Sharp and DeCarli41]. Understanding how rock-forming minerals transform under shock loading is critical for modelling collisions between planetary bodies, interpreting the significance of shock features in minerals and origins of commonly observed mesoscale material features, such as diaplectic (i.e., shocked) glass is critical to understanding many topics in geophysics, material science and planet formation[Reference Sharp and DeCarli41]. High pressure phases of water are relevant to understanding the structure and collisions of icy asteroids and comets[Reference Sharp and DeCarli41]. Formation of exotic phases, including the crystalline form of lonsdaleite during collision of celestial bodies, was predicted and recently confirmed experimentally using laser-driven shocks[Reference Kraus46]. Thus, studying WDM under dynamic compression relevant to these processes can also help us understand the origins of exotic materials and phase transitions.
Very strong temperature and pressure gradients are created in ICF implosions and can be seen in dense astrophysical objects. These gradients have a great influence on diffusion, conductivity, and subsequent mixing or de-mixing of different species present in the system. Heat and radiative transport through various layers influences the layer structure and convection of astrophysical objects, and electrical conductivity strongly affects magnetic fields generated by planetary core dynamos[Reference Olson47]. Recent experiments on MgO also confirmed a phase transition from electrically insulating solid to metallic liquid above 600 GPa showing that magmas inside terrestrial planets and super-Earths can be electrically conductive, enabling magnetic field-producing dynamo action within oxide-rich regions and blurring the distinction between planetary mantles and cores[Reference McWilliams39]. Thus the detailed knowledge transport properties of WDM states for various materials are crucial for the understanding of the origins of magnetic fields around planets as well as the internal layer structure. These phenomena have so far been explored mainly theoretically using computer simulations[Reference Militzer9, Reference Morales17]. In the case of ICF, the mixing of the DT fuel with the pellet material has already been observed experimentally[Reference Hurricane48, Reference Rygg49]. To date the most common techniques study the fuel mix from temporally and spatially resolved proton and neutron diagnostics as well as X-ray emission using tracer layers from the imploding pellets or indirectly from neutron yield[Reference Rygg49, Reference Regan50].
3 Experimental techniques
3.1 Generation of WDM
WDM can be created via a number of different approaches. One of the major challenges in generating WDM is to produce a large enough sample with uniform conditions. Strong gradients in temperature or density can create difficulty for probing and potentially make it impossible to make a reliable comparison with theoretical models. Another consideration is the time scale in which the WDM sample is generated and probed. Usually we wish to probe WDM under thermal equilibrium in order to compare it with EOS models for example for planetary interior structure studies. The kind of measurements require samples to be steady for time scales of hundreds of ps to ns as the collision time for ions is on the order of tens of ps. This is reasonable as the thermodynamic expansion is roughly equated to the speed of sound (
![]() ${\sim}10^{4}$
m/s) resulting in expansion time scales of tens of ns for millimetre scale targets. Some of the most commonly used schemes to generate WDM is thus the shock compression with energetic lasers with nanosecond duration on various materials[Reference Kritcher51], or more the recently developed laser-driven shock-and-release method[Reference Falk52]. Some studies, such as the transport properties of WDM, can specifically benefit from short-time scale measurements that allow to probe out-of-equilibrium systems. For these purposes femtosecond probes and isochoric heating techniques are more suitable. Alternatively, high power lasers and X-ray free electron lasers (XFELs) can be used to create dense homogeneously heated states by isochoric or volumetric heating using X-rays[Reference Glenzer53] or protons[Reference Patel54] generated by lasers. Static compression using laser-heated diamond anvil cells (DAC) has a very long history in the study of EOS and structure of high pressure states of matter[Reference Boehler1]. DACs have been used to achieve WDM states relevant to planetary interiors in regimes complementary to dynamically compressed matter[Reference Konôpková55]. In several advanced experiments the DAC technique was combined with dynamic compression with lasers to achieve even higher pressures[Reference Loubeyre56].
${\sim}10^{4}$
m/s) resulting in expansion time scales of tens of ns for millimetre scale targets. Some of the most commonly used schemes to generate WDM is thus the shock compression with energetic lasers with nanosecond duration on various materials[Reference Kritcher51], or more the recently developed laser-driven shock-and-release method[Reference Falk52]. Some studies, such as the transport properties of WDM, can specifically benefit from short-time scale measurements that allow to probe out-of-equilibrium systems. For these purposes femtosecond probes and isochoric heating techniques are more suitable. Alternatively, high power lasers and X-ray free electron lasers (XFELs) can be used to create dense homogeneously heated states by isochoric or volumetric heating using X-rays[Reference Glenzer53] or protons[Reference Patel54] generated by lasers. Static compression using laser-heated diamond anvil cells (DAC) has a very long history in the study of EOS and structure of high pressure states of matter[Reference Boehler1]. DACs have been used to achieve WDM states relevant to planetary interiors in regimes complementary to dynamically compressed matter[Reference Konôpková55]. In several advanced experiments the DAC technique was combined with dynamic compression with lasers to achieve even higher pressures[Reference Loubeyre56].
3.1.1 Dynamic compression
Solid or liquid samples can be compressed dynamically with shock or ramp compression to generate WDM conditions reaching solid densities, medium-to-high temperatures reaching from fractions of eV to 100 eV and pressures
![]() ${\sim}$
Mbar. In the case of shock compression we deal with abrupt changes in conditions across the shock front resulting in maximum possible compression creating conditions along the principal Hugoniot, which depends on the initial conditions of the material[Reference Zel’dovich and Raizer57]. Ramp compression on the other hand provides a more gentle pathway to reach high pressures and temperatures, which creates less entropy and with correct shaping of the drive can achieve isentropic compression creating conditions away from the Hugoniot curve[Reference Smith58]. Such ramped compression requires sophisticated pulse shaping capabilities. Alternatively, the shock-and-release method provides a route to create WDM states in a wide range of conditions to test the EOS models away from the principal Hugoniot[Reference Falk52, Reference Asay and Hayes59, Reference Knudson, Asay and Deeney60].
${\sim}$
Mbar. In the case of shock compression we deal with abrupt changes in conditions across the shock front resulting in maximum possible compression creating conditions along the principal Hugoniot, which depends on the initial conditions of the material[Reference Zel’dovich and Raizer57]. Ramp compression on the other hand provides a more gentle pathway to reach high pressures and temperatures, which creates less entropy and with correct shaping of the drive can achieve isentropic compression creating conditions away from the Hugoniot curve[Reference Smith58]. Such ramped compression requires sophisticated pulse shaping capabilities. Alternatively, the shock-and-release method provides a route to create WDM states in a wide range of conditions to test the EOS models away from the principal Hugoniot[Reference Falk52, Reference Asay and Hayes59, Reference Knudson, Asay and Deeney60].
One of the most common ways to create a shock with WDM conditions is by direct drive with high intensity lasers. When intense laser radiation is focused upon a solid/liquid target a fraction of its energy is immediately absorbed creating a hot, highly ionized, low density plasma (corona), which rapidly expands away from the solid surface into the vacuum with a time scale of a few picoseconds. This process is referred to as ablation, see Figure 2. Ablation creates strong pressure against the cold material, which drives a strong single shock into the target generating a steep density gradient. The most common ablator materials used in laser targets are different types of plastic. Inverse bremsstrahlung (IB) is the main process of absorption of the laser energy[Reference Kruer61]. During this process the laser beam interacts with the electrons moving within the Coulomb field of the ions and causes them to oscillate. Since the electrons have some thermal energy and associated velocity distribution they undergo random motion and collide with themselves and the surrounding ions. During these collisions, laser energy is transferred into thermal energy of the electrons as the extra laser-induced ordered oscillatory velocity gets randomized.
This collisional absorption mechanism dominates if the irradiance is kept below the limit of
![]() $I_{L}~(\text{W/cm}^{2})=3\times 10^{12}T_{e}~(\text{eV})/\unicode[STIX]{x1D706}^{2}~(\unicode[STIX]{x03BC}\text{m})\sim 4\times 10^{14}~\text{W/cm}^{2}$
[Reference Hughes and Nicholson-Florence62]. Shorter wavelengths are more advantageous as the laser light can propagate further into the plasma, closer to the cold material, and deposit its energy more efficiently. Laser absorption efficiencies reaching 80
$I_{L}~(\text{W/cm}^{2})=3\times 10^{12}T_{e}~(\text{eV})/\unicode[STIX]{x1D706}^{2}~(\unicode[STIX]{x03BC}\text{m})\sim 4\times 10^{14}~\text{W/cm}^{2}$
[Reference Hughes and Nicholson-Florence62]. Shorter wavelengths are more advantageous as the laser light can propagate further into the plasma, closer to the cold material, and deposit its energy more efficiently. Laser absorption efficiencies reaching 80
![]() $\%$
can be expected in such experiments[Reference Key and Spadling63]. If the laser irradiance reaches over the limit of
$\%$
can be expected in such experiments[Reference Key and Spadling63]. If the laser irradiance reaches over the limit of
![]() $I_{L}$
, the nature of the laser–plasma coupling changes and the incident radiation starts driving plasma waves within the target[Reference Key and Spadling63–Reference Ripin65]. If the temperature increases too much, the efficiency of the collisional absorption is reduced[Reference Kruer61]. Other absorption mechanisms such as the resonance absorption near the critical density
$I_{L}$
, the nature of the laser–plasma coupling changes and the incident radiation starts driving plasma waves within the target[Reference Key and Spadling63–Reference Ripin65]. If the temperature increases too much, the efficiency of the collisional absorption is reduced[Reference Kruer61]. Other absorption mechanisms such as the resonance absorption near the critical density
![]() $n_{c}$
also take place[Reference Kruer61, Reference Gibbon and Föster66]. However, laser interactions are a source of many instabilities that can decrease the efficiency of laser light absorption by reflecting the incident radiation away from the target surface preventing it from reaching the critical surface, e.g., stimulated Brillouin and Raman scattering[Reference Kruer61].
$n_{c}$
also take place[Reference Kruer61, Reference Gibbon and Föster66]. However, laser interactions are a source of many instabilities that can decrease the efficiency of laser light absorption by reflecting the incident radiation away from the target surface preventing it from reaching the critical surface, e.g., stimulated Brillouin and Raman scattering[Reference Kruer61].

Figure 2. Diagram of interaction between a solid/liquid target and a laser showing ablation of the surface material. The laser light can only propagate through the plasma up to the critical density
![]() $n_{c}$
at the critical surface, where it is reflected. The highest temperature is found at the critical surface. The temperature then drops between the critical surface and the solid target. Heat from the critical surface is conducted down the temperature gradient towards the solid surface, where it generates more plasma, keeping the ablation process going. The cooling process due to the rapid expansion is balanced by laser energy deposition keeping the temperature of the low density corona roughly constant. The region between the ablation and critical surfaces is often referred to as conduction zone.
$n_{c}$
at the critical surface, where it is reflected. The highest temperature is found at the critical surface. The temperature then drops between the critical surface and the solid target. Heat from the critical surface is conducted down the temperature gradient towards the solid surface, where it generates more plasma, keeping the ablation process going. The cooling process due to the rapid expansion is balanced by laser energy deposition keeping the temperature of the low density corona roughly constant. The region between the ablation and critical surfaces is often referred to as conduction zone.
Directly driven shocks require a very smooth laser profile, which can be achieved by randomly assigned phase and the use of polarization rotators[Reference Regan67]. Such phase plates break the laser beam into a number of smaller beamlets with different assigned phase change, which then interfere with one another producing much smoother spatial laser profile. This high frequency interference produces a speckle pattern with just few
![]() $\unicode[STIX]{x03BC}$
m features. As this process varies with the focusing optic parameters and laser wavelength, this system is more efficient for larger beams with a larger number of elements and higher energy due to better statistical averaging. Smoothing by spectral dispersion (SSD) is also used on some of the large laser systems[Reference Skupsky68]. The laser–plasma coupling efficiency is usually maximized by frequency doubled or tripled laser drive[Reference Kruer61]. The uniformity of the driven shocks can also be improved by the use of a thick pusher layer (usually quartz or Al)[Reference Hicks69]. The strength of a laser-driven shock is often measured by the ablation pressure. A simple scaling expression can be obtained from basic principles to calculate the approximate value of the expected ablation pressure[Reference Drake27]:
$\unicode[STIX]{x03BC}$
m features. As this process varies with the focusing optic parameters and laser wavelength, this system is more efficient for larger beams with a larger number of elements and higher energy due to better statistical averaging. Smoothing by spectral dispersion (SSD) is also used on some of the large laser systems[Reference Skupsky68]. The laser–plasma coupling efficiency is usually maximized by frequency doubled or tripled laser drive[Reference Kruer61]. The uniformity of the driven shocks can also be improved by the use of a thick pusher layer (usually quartz or Al)[Reference Hicks69]. The strength of a laser-driven shock is often measured by the ablation pressure. A simple scaling expression can be obtained from basic principles to calculate the approximate value of the expected ablation pressure[Reference Drake27]:
which yields values of 3.5 Mbar and 16 Mbar for irradiances of
![]() $10^{13}$
and
$10^{13}$
and
![]() $10^{14}~\text{W}/\text{cm}^{2}$
. These values are however likely to be slightly too high. A better estimate of the ablation pressure can be obtained by scaling expressions obtained in past experiments[Reference Key70, Reference Fabbro71]. This pressure then generates a strong shock wave moving into the unperturbed material behind the ablator, which compresses the material to higher densities depending on the initial conditions and the material. The temperature of the plasma increases due to shock heating, which depends on the pressure in the shock wave. These shocks readily create relatively steady WDM conditions over tens to hundreds of
$10^{14}~\text{W}/\text{cm}^{2}$
. These values are however likely to be slightly too high. A better estimate of the ablation pressure can be obtained by scaling expressions obtained in past experiments[Reference Key70, Reference Fabbro71]. This pressure then generates a strong shock wave moving into the unperturbed material behind the ablator, which compresses the material to higher densities depending on the initial conditions and the material. The temperature of the plasma increases due to shock heating, which depends on the pressure in the shock wave. These shocks readily create relatively steady WDM conditions over tens to hundreds of
![]() $\unicode[STIX]{x03BC}$
m propagating through targets for several nanoseconds, which allows reliable measurement of steady-state conditions.
$\unicode[STIX]{x03BC}$
m propagating through targets for several nanoseconds, which allows reliable measurement of steady-state conditions.
The primary challenge with directly driven shocks by lasers is preheating of unperturbed material, mainly radiative preheating with X-rays from the plasma at the laser–solid interaction which gets heated to keV temperatures. Such thermal emission in the X-ray region can easily penetrate tens of
![]() $\unicode[STIX]{x03BC}$
m into solid material and heat the target ahead of the shock wave. This then modifies the initial conditions of the shock wave changing the Hugoniot conditions and with it the final shocked state. Since this initial preheated state is usually unknown, this situation renders the EOS measurement useless. The radiative preheating in the target by high energy X-rays can be mitigated by adding a thin radiation shield (e.g.,
$\unicode[STIX]{x03BC}$
m into solid material and heat the target ahead of the shock wave. This then modifies the initial conditions of the shock wave changing the Hugoniot conditions and with it the final shocked state. Since this initial preheated state is usually unknown, this situation renders the EOS measurement useless. The radiative preheating in the target by high energy X-rays can be mitigated by adding a thin radiation shield (e.g.,
![]() ${\sim}2$
–
${\sim}2$
–
![]() $3~\unicode[STIX]{x03BC}\text{m}$
Au) behind the ablator that will stop the radiation from propagating into the unshocked target[Reference Falk52]. Thick Al layers are also used to reduce radiative preheating and avoid reverberations of shocks[Reference Hicks69]. Preheating can also come from hot electrons created by filamentation or stimulated Raman scattering in the low density plasma in the corona or from thermal electrons originating from the hot plasma at the critical surface[Reference Kruer61, Reference Trainor and Lee72, Reference Falk73].
$3~\unicode[STIX]{x03BC}\text{m}$
Au) behind the ablator that will stop the radiation from propagating into the unshocked target[Reference Falk52]. Thick Al layers are also used to reduce radiative preheating and avoid reverberations of shocks[Reference Hicks69]. Preheating can also come from hot electrons created by filamentation or stimulated Raman scattering in the low density plasma in the corona or from thermal electrons originating from the hot plasma at the critical surface[Reference Kruer61, Reference Trainor and Lee72, Reference Falk73].
Some good examples of laboratory astrophysics experiments with ablatively driven shock on large laser systems including the measurement of conductivity of dynamically compressed water relevant to the interior of Neptune were carried out by Celliers et al. [Reference Celliers74] and Koenig et al. [Reference Koenig75]. The high pressure melt transition in Fe at conditions similar to those found on the boundary of the outer and inner core of Earth has also been studied by dynamic compression methods with high power lasers[Reference Nguyen and Holmes5, Reference Koenig75, Reference Benuzzi-Mounaix76]. Even more extreme conditions can be achieved by letting two shock waves collide as shown by Zastrau et al. on warm dense carbon measurements[Reference Zastrau77].
One of the alternatives to drive strong shocks in solid targets is to use a gold cavity (hohlraum) heated by optical lasers that irradiate the samples with X-rays that can then ablatively drive the shock in the same manner to direct laser illumination, but with better uniformity[Reference Kraus78]. This approach is similar to that for ICF where DT fuel pellets are imploded with intense X-ray radiation inside a gold hohlraum[Reference Nuckolls6]. This can be very efficient as high
![]() $Z$
materials like gold are very bright X-ray sources, especially in the sub-keV regime with conversion efficiency of up to 80%[Reference Kania79]. Kraus et al. used this approach to strongly compress polystyrene to WDM conditions and measure its temperature and ionization balance at pressures exceeding 100 Mbar[Reference Kraus78]. One advantage of this method is the mitigation of preheat caused by fast electrons created in the optical laser–plasma interaction at high laser intensities that cannot escape the high
$Z$
materials like gold are very bright X-ray sources, especially in the sub-keV regime with conversion efficiency of up to 80%[Reference Kania79]. Kraus et al. used this approach to strongly compress polystyrene to WDM conditions and measure its temperature and ionization balance at pressures exceeding 100 Mbar[Reference Kraus78]. One advantage of this method is the mitigation of preheat caused by fast electrons created in the optical laser–plasma interaction at high laser intensities that cannot escape the high
![]() $Z$
X-ray generation target, which means that the indirect drive ICF has a significant advantage to generate more uniform plasma conditions.
$Z$
X-ray generation target, which means that the indirect drive ICF has a significant advantage to generate more uniform plasma conditions.
Another option to dynamically compress matter is to use flyer plates, which can be launched by direct or indirect ablation[Reference Cauble80]. The flyer plate impacts the secondary target at high speeds generating a strong shock wave that compresses and heats the material. Knudson et al. have developed a novel method of magnetically launching flyer plates using z-pinches to generate WDM states[Reference Knudson, Asay and Deeney60, Reference Knudson81, Reference Knudson, Desjarlais and Dolan82]. In these experiments with a time scale of
![]() ${\sim}100$
–600 ns, a DC current of
${\sim}100$
–600 ns, a DC current of
![]() ${\sim}20$
MA is delivered to short circuited loads generating strong magnetic fields and pressures exceeding 1200 T and 600 GPa, respectively. Such magnetic pressure can then be used to launch a flyer plate to ultrahigh velocity in a plate impact experiment. The impact of this plate on a planar target induces a multi-Mbar shock wave. Knudson et al. were able to study EOS of deuterium to 400 GPa[Reference Knudson81] and the high pressure phases of carbon, specifically the diamond melt line under WDM conditions using this method[Reference Knudson, Desjarlais and Dolan82]. The use of a flyer plate also allows a measurement of its speed that can be used to directly obtain the particle and shock velocity relationship for the Hugoniot relations in Equation (2) and thus derive an EOS relationship for the principal Hugoniot for optical diagnostics[Reference Knudson and Desjarlais83]. This method is discussed in more detail in the following section. Such experiments have the advantage of potentially removing the preheat, but they can suffer from significant hydrodynamic instabilities which could lead to nonuniform impact of the plate onto the secondary target. Older approaches to dynamically drive shocks to WDM regime also employ gas guns[Reference Holmes84] or explosives[Reference Boriskov21]. A novel design of compact gas-gun system was recently synchronized with synchrotron systems to study high-compression states with X-ray imaging and diffraction techniques[Reference Luo85, Reference Fan86]. Direct implosion of z-pinch plasmas can also be used to create and study WDM states[Reference Benage, Shanahan and Murillo87].
${\sim}20$
MA is delivered to short circuited loads generating strong magnetic fields and pressures exceeding 1200 T and 600 GPa, respectively. Such magnetic pressure can then be used to launch a flyer plate to ultrahigh velocity in a plate impact experiment. The impact of this plate on a planar target induces a multi-Mbar shock wave. Knudson et al. were able to study EOS of deuterium to 400 GPa[Reference Knudson81] and the high pressure phases of carbon, specifically the diamond melt line under WDM conditions using this method[Reference Knudson, Desjarlais and Dolan82]. The use of a flyer plate also allows a measurement of its speed that can be used to directly obtain the particle and shock velocity relationship for the Hugoniot relations in Equation (2) and thus derive an EOS relationship for the principal Hugoniot for optical diagnostics[Reference Knudson and Desjarlais83]. This method is discussed in more detail in the following section. Such experiments have the advantage of potentially removing the preheat, but they can suffer from significant hydrodynamic instabilities which could lead to nonuniform impact of the plate onto the secondary target. Older approaches to dynamically drive shocks to WDM regime also employ gas guns[Reference Holmes84] or explosives[Reference Boriskov21]. A novel design of compact gas-gun system was recently synchronized with synchrotron systems to study high-compression states with X-ray imaging and diffraction techniques[Reference Luo85, Reference Fan86]. Direct implosion of z-pinch plasmas can also be used to create and study WDM states[Reference Benage, Shanahan and Murillo87].
3.1.2 Static compression
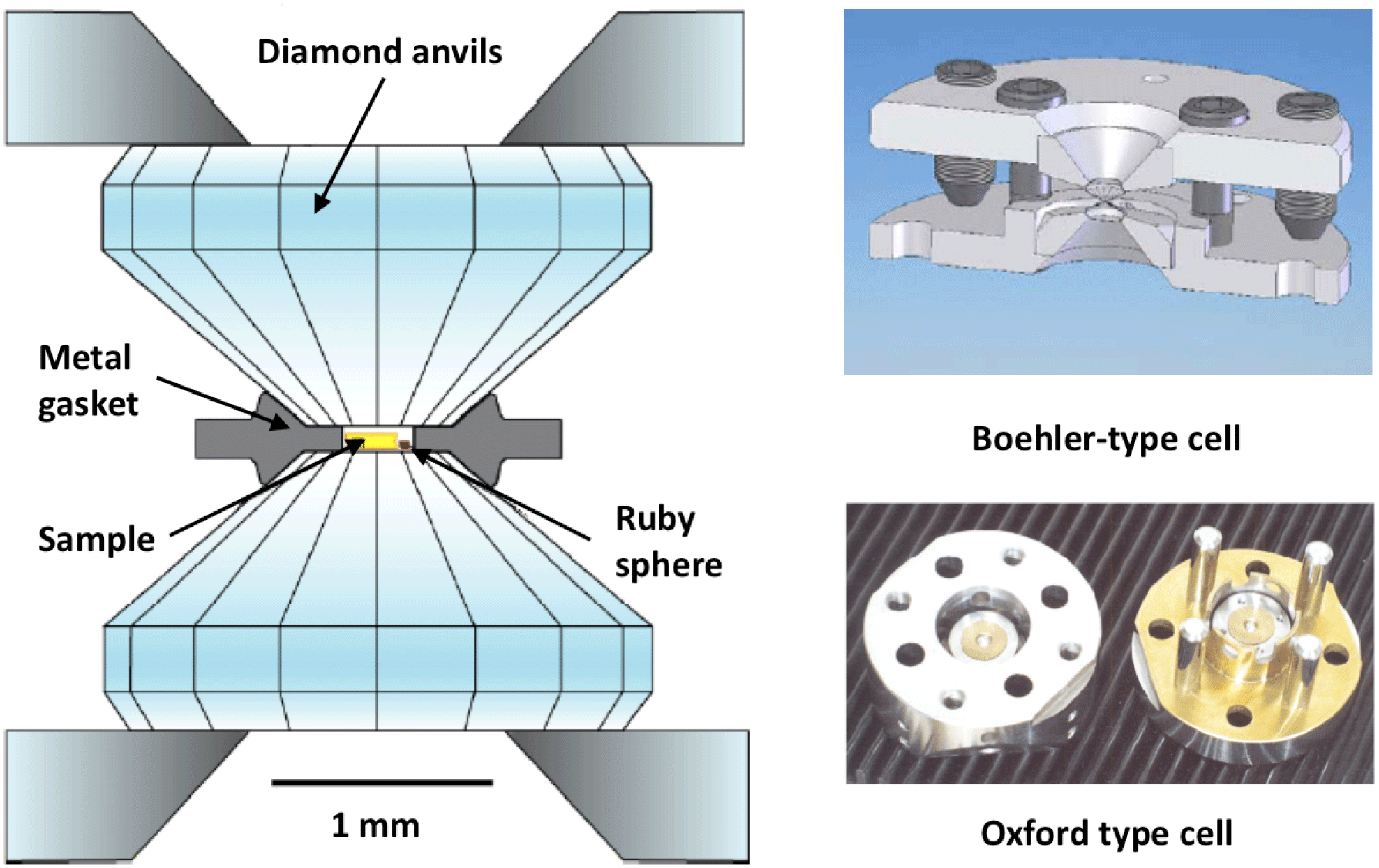
The diamond anvil cell (DAC) was first developed by Weir et al. [Reference Weir88, Reference Bassett89] as a new technique in high pressure physics research and geoscience. Other materials such as sapphire have been used in similar applications, but diamond due to its strength and hardness is the material of choice to achieve the highest pressures reaching the Mbar range. Another advantage leading to the choice of the anvil material is the transparency to electromagnetic radiation in the infrared (IR), optical, ultraviolet (UV) and X-ray bands used as diagnostic probes, which allows various diagnostic techniques to study material structures and conditions relevant to planetary interiors as described by Mao and Hemley[Reference Mao and Hemley90]. The three main types of DAC systems are the piston-cylinder Mao–Bell cell, Merrill–Bassett type and the Boehler–Almax (plate) cell. A typical DAC setup is shown in Figure 3 where two opposing diamond anvils, perfectly polished diamonds with a flat culets facing each other, compress a metal gasket (flat foil with a drilled hole) that contains the sample. Typical materials used as gaskets are: rhenium, tungsten, stainless steel type 301, and beryllium. DACs have been able to reach thousands K and at least a few GPa already since their invention in 1959[Reference Boehler1]. Typically DACs reach up to few hundreds of GPa, although pressures beyond 1 TPa (10 Mbar) have recently been achieved with double-stage diamond anvil cells[Reference Dubrovinskaia91].
One or two small chromium-doped ruby (Al
![]() $_{2}$
O
$_{2}$
O
![]() $_{3}$
:Cr
$_{3}$
:Cr
![]() $^{3+}$
) spheres are also buried inside the gasket with the sample. These act as a pressure reference, which was first introduced by Barnett et al.
[Reference Barnett92], who discovered the near-linear relationship of the spectral shifts of the optical fluorescence lines of ruby with increasing pressure. This secondary pressure scale is then used as a reliable pressure gauge in DAC experiments[Reference Syassen93]. These measurements are relatively straightforward at
$^{3+}$
) spheres are also buried inside the gasket with the sample. These act as a pressure reference, which was first introduced by Barnett et al.
[Reference Barnett92], who discovered the near-linear relationship of the spectral shifts of the optical fluorescence lines of ruby with increasing pressure. This secondary pressure scale is then used as a reliable pressure gauge in DAC experiments[Reference Syassen93]. These measurements are relatively straightforward at
![]() $P<100$
GPa and can be carried out online or offline using a calibrated grating spectrometer coupled with an optical laser system, which can be focused onto the ruby spheres inside the gaskets under a microscope. The temperature of these statically compressed samples can be increased to
$P<100$
GPa and can be carried out online or offline using a calibrated grating spectrometer coupled with an optical laser system, which can be focused onto the ruby spheres inside the gaskets under a microscope. The temperature of these statically compressed samples can be increased to
![]() ${\sim}5000$
K (
${\sim}5000$
K (
![]() ${\sim}0.4$
eV) by continuous-wave (cw) or pulsed infrared laser heating[Reference Konôpková55, Reference Deemyad and Silvera94]. Pulsed laser heating has several advantages over cw heating as it can suppress thermally activated diffusion into the gasket and diamond, suppress chemical reactions of impurities with the sample and environment, require far less average power and thus less heating of the sample environment, and can reach higher temperatures. The main limitation of the static compression with classical DAC is that it cannot access majority of the WDM conditions. DAC research is however complementary to the dynamic compression experiments and combinations of both techniques allow access to even more extreme conditions.
${\sim}0.4$
eV) by continuous-wave (cw) or pulsed infrared laser heating[Reference Konôpková55, Reference Deemyad and Silvera94]. Pulsed laser heating has several advantages over cw heating as it can suppress thermally activated diffusion into the gasket and diamond, suppress chemical reactions of impurities with the sample and environment, require far less average power and thus less heating of the sample environment, and can reach higher temperatures. The main limitation of the static compression with classical DAC is that it cannot access majority of the WDM conditions. DAC research is however complementary to the dynamic compression experiments and combinations of both techniques allow access to even more extreme conditions.

Figure 3. Schematic of a typical DAC setup including the diamond anvils, metal gasket, sample and a ruby sphere pressure reference. The figure also includes some examples of different cell/gear box systems used.
Typical diagnostics used with such statically compressed samples include single crystal or powder X-ray diffraction at synchrotron facilities used to study the structure and the EOS of crystalline samples such as single-crystal hydrogen at extreme pressures[Reference Mao95]. Alternatively, Raman or IR spectroscopy is used for finger-printing and structural studies of molecular substances through observation of energy shifts due to the vibrational and rotational modes of the molecular bonds[Reference Silvera96]. Tateno et al. used laser-heated DAC to compress solid iron to the conditions inside Earth’s core at 377 GPa and 5700 K (
![]() ${\sim}0.5$
eV) for the first time[Reference Tateno97]. Kon̂opková et al. have recently carried out direct measurements of thermal conductivity of solid Fe dynamically heated by a laser inside a DAC under conditions predicted for terrestrial planets by thermal emission[Reference Konôpková55]. Merkel et al. have used DAC to plastically deform polycrystalline MgGeO
${\sim}0.5$
eV) for the first time[Reference Tateno97]. Kon̂opková et al. have recently carried out direct measurements of thermal conductivity of solid Fe dynamically heated by a laser inside a DAC under conditions predicted for terrestrial planets by thermal emission[Reference Konôpková55]. Merkel et al. have used DAC to plastically deform polycrystalline MgGeO
![]() $_{3}$
and (Mg
$_{3}$
and (Mg
![]() $_{0.9}$
,Fe
$_{0.9}$
,Fe
![]() $_{0.1}$
)SiO
$_{0.1}$
)SiO
![]() $_{3}$
post-perovskites at 145–157 GPa and 104–130 GPa, respectively, with heating to maximum temperature of 2000 K (
$_{3}$
post-perovskites at 145–157 GPa and 104–130 GPa, respectively, with heating to maximum temperature of 2000 K (
![]() ${\sim}0.2$
eV)[Reference Merkel98, Reference Merkel99]. The structural measurements were carried out with X-ray diffraction at the Advanced Photon Source and compared with seismic observation studying the behaviour at Earth’s lower mantle conditions.
${\sim}0.2$
eV)[Reference Merkel98, Reference Merkel99]. The structural measurements were carried out with X-ray diffraction at the Advanced Photon Source and compared with seismic observation studying the behaviour at Earth’s lower mantle conditions.
New experiments carried out at the Lawrence Livermore National Laboratory (LLNL) in California that combine both compression techniques, where statically pre-compressed DACs are further compressed and heated by laser-driven shock wave have also been reported and shown to be a promising tool to probe the hydrogen EOS to even more extreme pressures and temperatures in the WDM regime[Reference Loubeyre56, Reference Loubeyre100]. Interesting work was also done on pre-compressed helium and water samples shock-driven to up to
![]() ${\sim}10$
Mbar (1000 GPa) pressures with laser-driven shocks[Reference Eggert101–Reference Henry104]. The main advantage of this combination of techniques is that significantly higher pressures can be reached while keeping moderate temperatures relevant to planetary interiors. The disadvantage is that this approach requires a very high laser energy, which only few facilities in the world can accommodate.
${\sim}10$
Mbar (1000 GPa) pressures with laser-driven shocks[Reference Eggert101–Reference Henry104]. The main advantage of this combination of techniques is that significantly higher pressures can be reached while keeping moderate temperatures relevant to planetary interiors. The disadvantage is that this approach requires a very high laser energy, which only few facilities in the world can accommodate.
3.1.3 Isochoric heating
Generation of X-ray sources and proton beams using lasers has been of a great interest to the WDM community in the recent years since X-rays and protons can be used to create isochorically heated states that are homogeneous, i.e., easy to probe[Reference Glenzer53, Reference Patel54]. Heating with optical lasers has also been demonstrated experimentally, but such samples need to be kept extremely thin (10–100 nm) in order to ensure uniform heating[Reference Dorchies105]. Ion beams and X-rays, in contrast to lasers, can penetrate deep inside solid-density material, thereby heating macroscopic samples to extreme states while keeping the density gradients low and close to the initial, well known density[Reference Hoffmann106]. Most commonly isochorically heated WDM is created with X-ray sources due to the fact that such sources are more abundant and easier to manipulate[Reference Glenzer53, Reference Nagler107, Reference Fäustlin108]. Achieving good heating uniformity requires a sufficiently long photon absorption length for samples that are usually tens to hundreds of
![]() $\unicode[STIX]{x03BC}$
m thick. Thus, for volumetric heating with X-rays to WDM regime we are generally interested in harder regime of
$\unicode[STIX]{x03BC}$
m thick. Thus, for volumetric heating with X-rays to WDM regime we are generally interested in harder regime of
![]() ${>}1$
keV, which can be generated with a few percent efficiency from L-shell emission from mid-
${>}1$
keV, which can be generated with a few percent efficiency from L-shell emission from mid-
![]() $Z$
elements heated by a laser[Reference Phillion and Hailey109].
$Z$
elements heated by a laser[Reference Phillion and Hailey109].
A typical example of a WDM experiment with laser-generated L-shell radiation heating can be seen in the work by Glenzer et al.
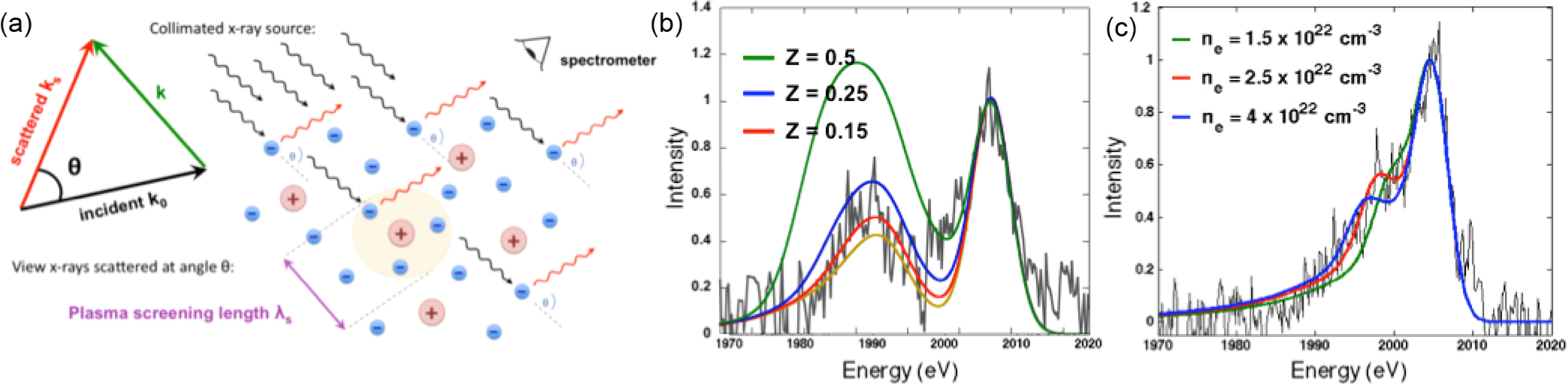
[Reference Glenzer53, Reference Glenzer110]. During their first experiment, they were able to create strongly coupled warm dense Be with partial electron degeneracy using emission from Rh at 2.7–3.4 keV. Thermodynamic conditions of
![]() ${\sim}3\times 10^{23}~\text{cm}^{-3}$
and 53 eV were measured by noncollective X-ray Thomson scattering (XRTS) discussed in the following section[Reference Glenzer53]. This experiment was then repeated with heating from Ag achieving similar densities and temperatures of 12 eV, but this time with collective XRTS measurement[Reference Glenzer110]. Recently, temperatures around 1 eV at solid densities were achieved on Al using Pd L-shell radiation in order to study XUV opacity by Kettle et al.
[Reference Kettle111]. Gold hohlraum similar to those used in ICF was designed to heat solid-density carbon foams by supersonic soft X-ray (
${\sim}3\times 10^{23}~\text{cm}^{-3}$
and 53 eV were measured by noncollective X-ray Thomson scattering (XRTS) discussed in the following section[Reference Glenzer53]. This experiment was then repeated with heating from Ag achieving similar densities and temperatures of 12 eV, but this time with collective XRTS measurement[Reference Glenzer110]. Recently, temperatures around 1 eV at solid densities were achieved on Al using Pd L-shell radiation in order to study XUV opacity by Kettle et al.
[Reference Kettle111]. Gold hohlraum similar to those used in ICF was designed to heat solid-density carbon foams by supersonic soft X-ray (
![]() ${<}2$
keV) heat wave generated in an EOS experiment carried out by Gregori et al.
[Reference Gregori112].
${<}2$
keV) heat wave generated in an EOS experiment carried out by Gregori et al.
[Reference Gregori112].
With the dawn of free electron lasers, new types of experiments became possible. These beams have an ultrashort duration of tens of femtoseconds and extremely high brightness, which provides additional interesting insight into the nonequilibrium dynamics of WDM. An interesting example is the demonstration of transparency of warm dense Al to XUV radiation resulting from short lifetime of the excited states leading to a saturable absorption of L-shell transitions[Reference Nagler107]. The first volumetric heating using the soft X-ray beam to heat cryogenic hydrogen samples to WDM states relevant to planetary interiors combined with collective XRTS measurement, yielding a temperature of 13 eV and electron density of
![]() $2.8\times 10^{20}$
cm
$2.8\times 10^{20}$
cm
![]() $^{-3}$
, was done at the FLASH facility by Fäustlin et al.
[Reference Fäustlin108]. The main disadvantage of using these soft X-ray lasers is the very short absorption length requiring very thin samples or resulting in nonuniform heating. More recently, new facilities such as the Linac Coherent Light Source (LCLS) at Stanford University, SACLA in Japan or the European X-FEL in Germany are capable of reaching tuneable X-ray beams in the range of 2–15 keV with
$^{-3}$
, was done at the FLASH facility by Fäustlin et al.
[Reference Fäustlin108]. The main disadvantage of using these soft X-ray lasers is the very short absorption length requiring very thin samples or resulting in nonuniform heating. More recently, new facilities such as the Linac Coherent Light Source (LCLS) at Stanford University, SACLA in Japan or the European X-FEL in Germany are capable of reaching tuneable X-ray beams in the range of 2–15 keV with
![]() $10^{12}$
photons in a pulse that can reach uniform volumetric heating like in Refs. [Reference Lévy113–Reference Ciricosta115]. Hau-Riege et al. observed transitions from solid to liquid and plasma states in isochorically heated graphite at LCLS[Reference Hau-Riege116]. Sperling et al. have been able to obtain a robust measurement of electron density, temperature, plasmon frequency and damping of warm dense Al heated isochorically by the LCLS X-ray beam with collective XRTS and use these results to determine the dynamical electrical conductivity[Reference Sperling117].
$10^{12}$
photons in a pulse that can reach uniform volumetric heating like in Refs. [Reference Lévy113–Reference Ciricosta115]. Hau-Riege et al. observed transitions from solid to liquid and plasma states in isochorically heated graphite at LCLS[Reference Hau-Riege116]. Sperling et al. have been able to obtain a robust measurement of electron density, temperature, plasmon frequency and damping of warm dense Al heated isochorically by the LCLS X-ray beam with collective XRTS and use these results to determine the dynamical electrical conductivity[Reference Sperling117].
Laser–ion acceleration is primarily driven by relativistic electrons, generated by the interaction of an ultraintense laser beam with a solid target. The laser peak intensity thereby has to exceed
![]() $10^{18}~\text{W/cm}^{2}$
to immediately accelerate electrons close to the speed of light. Modern lasers are able to reach maximum intensities of more than
$10^{18}~\text{W/cm}^{2}$
to immediately accelerate electrons close to the speed of light. Modern lasers are able to reach maximum intensities of more than
![]() $10^{21}~\text{W/cm}^{2}$
[Reference Bahk118]. Examples of laser-driven ion acceleration for isochoric heating applications are shown in Fig. 4. The dominant ion acceleration starts off the rear, nonirradiated surface by a rapid charge separation driven by a mechanism known as target normal sheath acceleration (TNSA)[Reference Wilks119]. This scheme primarily accelerates ions from the surface of the target. Ions accelerated by TNSA have an exponential energy distribution with an upper cut-off energy determined by the maximum of the accelerating electric potential. Conversion efficiencies of 10% have been reported[Reference Wagner120]. Access to higher energy ranges has been proposed by a set of new acceleration mechanisms, all based on ultraintense laser–matter interaction: radiation pressure acceleration (RPA)[Reference Robinson121], and laser break-out afterburner (BOA)[Reference Palaniyappan122]. The RPA mechanism is very demanding to the driving laser system. It requires focal spot intensities exceeding
$10^{21}~\text{W/cm}^{2}$
[Reference Bahk118]. Examples of laser-driven ion acceleration for isochoric heating applications are shown in Fig. 4. The dominant ion acceleration starts off the rear, nonirradiated surface by a rapid charge separation driven by a mechanism known as target normal sheath acceleration (TNSA)[Reference Wilks119]. This scheme primarily accelerates ions from the surface of the target. Ions accelerated by TNSA have an exponential energy distribution with an upper cut-off energy determined by the maximum of the accelerating electric potential. Conversion efficiencies of 10% have been reported[Reference Wagner120]. Access to higher energy ranges has been proposed by a set of new acceleration mechanisms, all based on ultraintense laser–matter interaction: radiation pressure acceleration (RPA)[Reference Robinson121], and laser break-out afterburner (BOA)[Reference Palaniyappan122]. The RPA mechanism is very demanding to the driving laser system. It requires focal spot intensities exceeding
![]() $10^{22}~\text{W/cm}^{2}$
and circular polarization of the laser light, which is beyond the reach of today’s laser systems. The BOA mechanism on the other hand only requires
$10^{22}~\text{W/cm}^{2}$
and circular polarization of the laser light, which is beyond the reach of today’s laser systems. The BOA mechanism on the other hand only requires
![]() $10^{20}~\text{W/cm}^{2}$
, linear polarization and a high temporal contrast of the pulse, see Fig. 4(b). Therefore, this mechanism can be tested already using present laser facilities with a pulse length of 500 fs and energy of about 100 J on target.
$10^{20}~\text{W/cm}^{2}$
, linear polarization and a high temporal contrast of the pulse, see Fig. 4(b). Therefore, this mechanism can be tested already using present laser facilities with a pulse length of 500 fs and energy of about 100 J on target.

Figure 4. Laser–ion acceleration for isochoric heating: (a) a curved target for focusing of ion beams for isochoric heating to generate WDM as used by Patel et al. [Reference Patel54], (b) a typical deuteron BOA spectrum taken at the Trident laser facility obtained by the iWASP diagnostic[Reference Jung123].
An important consideration in WDM generation with proton heating is the precise knowledge of the energy deposition in the sample, which has so far only very limited data[Reference Hoffmann106, Reference Zylstra124]. Roth et al. have worked on the investigation of ion energy deposition in solids and plasmas for more than 20 years using the heavy ion accelerator UNILAC at the GSI Helmholtzzentrum fur Schwerionenforschung[Reference Stoeckl125–Reference Cayzac128]. An important consideration is the broad spectrum of the protons created with laser acceleration schemes (typically 5–15 MeV) resulting in a large temporal dispersion of the beam of the order of tens of ps only a couple of mm away from the target. This fact makes it more complicated to simultaneously reach the isochoric conditions and obtain high temperatures. This means that such experiments require very small scale targets with the secondary heated targets being located not further than 1 mm away from the laser proton source. This can be a challenge for diagnostic systems as at such close proximity to the primary laser target hot plasma blows off and fast electrons can interfere with the measurement and could cause issues for electronic detectors through the generation of strong electromagnetic pulses (EMP).
The first experiment using proton heating to create WDM states in 10
![]() $\unicode[STIX]{x03BC}$
m thick Al foil was carried out by Patel et al.
[Reference Patel54] see Fig. 4(a). The experiment used TNSA protons with an energy range of 4–12 MeV to heat the sample. Since these beams have some divergence, a focusing scheme with a hemi-spherical target was tested. The temperature of the heated foil was determined using optical pyrometry (see the following section) and found to be 4 eV with unfocused proton beam and 23 eV with focused heating. Pelka et al. used proton heating to isochorically melt carbon to the WDM regime[Reference Pelka129]. They used X-ray Thomson scattering to measure the EOS at conditions relevant to carbon-rich interiors of ice giants and their magnetic field generation. More recently, White et al. isochorically heated macroscopic graphite crystals generating temperatures close to the melting threshold (1.5 eV) with laser-produced proton beams[Reference White130]. They used time-resolved X-ray diffraction to study dynamic coupling between electrons and ions in nonequilibrium WDM discovering three time longer relaxation time than previously reported indicating an energy transfer bottleneck.
$\unicode[STIX]{x03BC}$
m thick Al foil was carried out by Patel et al.
[Reference Patel54] see Fig. 4(a). The experiment used TNSA protons with an energy range of 4–12 MeV to heat the sample. Since these beams have some divergence, a focusing scheme with a hemi-spherical target was tested. The temperature of the heated foil was determined using optical pyrometry (see the following section) and found to be 4 eV with unfocused proton beam and 23 eV with focused heating. Pelka et al. used proton heating to isochorically melt carbon to the WDM regime[Reference Pelka129]. They used X-ray Thomson scattering to measure the EOS at conditions relevant to carbon-rich interiors of ice giants and their magnetic field generation. More recently, White et al. isochorically heated macroscopic graphite crystals generating temperatures close to the melting threshold (1.5 eV) with laser-produced proton beams[Reference White130]. They used time-resolved X-ray diffraction to study dynamic coupling between electrons and ions in nonequilibrium WDM discovering three time longer relaxation time than previously reported indicating an energy transfer bottleneck.
An alternative scheme with electrons has also been proposed[Reference Bell131]. Fast electrons are able to penetrate deep into the targets hundreds of
![]() $\unicode[STIX]{x03BC}$
m thick. Such fast electron current can exceed the Alfvén limit generating a balancing return current at lower energy. These lower energy electrons are more collisional and can generate temperatures reaching tens of eV through resistive heating of the sample. This process has already been used to generate WDM with strong ion–ion coupling and partial electron degeneracy[Reference Hansen132]. The main limitation of this technique is the close proximity of the electron acceleration target and the heated sample, which is even more strict than in the case of laser-generated protons. At such short distances we start dealing with additional issues including high temperature nonuniform plasma blow off from the primary target, hard X-ray background, and EMP that can affect the diagnostics.
$\unicode[STIX]{x03BC}$
m thick. Such fast electron current can exceed the Alfvén limit generating a balancing return current at lower energy. These lower energy electrons are more collisional and can generate temperatures reaching tens of eV through resistive heating of the sample. This process has already been used to generate WDM with strong ion–ion coupling and partial electron degeneracy[Reference Hansen132]. The main limitation of this technique is the close proximity of the electron acceleration target and the heated sample, which is even more strict than in the case of laser-generated protons. At such short distances we start dealing with additional issues including high temperature nonuniform plasma blow off from the primary target, hard X-ray background, and EMP that can affect the diagnostics.
3.2 Diagnostic methods
Due to the high density and relatively low temperature the experimental measurements of thermodynamic conditions and structure in WDM are challenging. This section discusses the different diagnostic methods that are used to studying various properties of WDM under laboratory astrophysics settings. We focus mostly on high power laser facilities, but these systems are used on z-pinches or free electrons lasers and other facilities dedicated to studying WDM as well. The use of different diagnostics also provides a natural break down of the whole field into smaller segments dedicated to different types of work as researchers usually specialize in one or two kinds of these techniques to study some specific properties well matched to the instruments used.
3.2.1 Optical probes
The velocity interferometry system for any reflector (VISAR) is a standard diagnostic used to measure the velocity of a reflecting surface through Doppler effect[Reference Takeda, Ina and Kobayashi133]. In shock wave experiments, it is commonly employed to get shock
![]() $U_{s}$
or particle
$U_{s}$
or particle
![]() $U_{p}$
velocities. These quantities are very important since the thermodynamic state of the shocked sample can then be obtained using the Hugoniot relations in conjunction with EOS tables as shown below[Reference Celliers134]. In the case that shock and particle velocity can be obtained, the sample EOS can be measured. Another common approach to access to EOS is to do a relative measurement, where shock velocity is measured both in the sample and in a reference material. Shock velocity is directly obtained in transparent materials and for strong shocks. In this case, the sample is highly ionized and can become reflective to optical radiation. The optical probe of the VISARs systems is therefore directly reflected from the shock front, giving access to the shock velocity. For weaker shocks or for nontransparent materials, VISARs often measure interface velocities, from which particle velocity can be accessed, provided that the refractive index of the material behind the interface is known.
$U_{p}$
velocities. These quantities are very important since the thermodynamic state of the shocked sample can then be obtained using the Hugoniot relations in conjunction with EOS tables as shown below[Reference Celliers134]. In the case that shock and particle velocity can be obtained, the sample EOS can be measured. Another common approach to access to EOS is to do a relative measurement, where shock velocity is measured both in the sample and in a reference material. Shock velocity is directly obtained in transparent materials and for strong shocks. In this case, the sample is highly ionized and can become reflective to optical radiation. The optical probe of the VISARs systems is therefore directly reflected from the shock front, giving access to the shock velocity. For weaker shocks or for nontransparent materials, VISARs often measure interface velocities, from which particle velocity can be accessed, provided that the refractive index of the material behind the interface is known.
One of the most advanced systems of this type was deployed at the OMEGA laser facility as described by Celliers et al.
[Reference Celliers134]. The main components of the VISAR diagnostic are: a probe laser (in this case the wavelength
![]() $\unicode[STIX]{x1D706}\sim 500$
nm, but infrared laser sources are often used), an imaging system and one or two Mach–Zehnder interferometers. The imaging system conveys the probe beam to the target, where it reflects back onto the output beam splitter in the interferometer. The interferometer system generates a linear fringe pattern formed by the interference between the laser beams passing through the two interferometer arms with a different delay. The shape and density of the fringe pattern are controlled by a slight tilt of the output beam splitter. The interferometer setup and the typical VISAR streak image are shown in Figure 5. The output from both interferometers is detected with an optical streak camera with one spatial and one temporal dimension with
$\unicode[STIX]{x1D706}\sim 500$
nm, but infrared laser sources are often used), an imaging system and one or two Mach–Zehnder interferometers. The imaging system conveys the probe beam to the target, where it reflects back onto the output beam splitter in the interferometer. The interferometer system generates a linear fringe pattern formed by the interference between the laser beams passing through the two interferometer arms with a different delay. The shape and density of the fringe pattern are controlled by a slight tilt of the output beam splitter. The interferometer setup and the typical VISAR streak image are shown in Figure 5. The output from both interferometers is detected with an optical streak camera with one spatial and one temporal dimension with
![]() $\unicode[STIX]{x03BC}$
m spatial and ps temporal resolution, respectively. The streak camera thus provides a continuous record of the shock evolution for several nanoseconds. An optical delay element (etalon) is added to one of the arms in the interferometer setup. This introduces an additional optical path delay to the reflected probe beam while keeping the spatial coherence, which is easy to control.
$\unicode[STIX]{x03BC}$
m spatial and ps temporal resolution, respectively. The streak camera thus provides a continuous record of the shock evolution for several nanoseconds. An optical delay element (etalon) is added to one of the arms in the interferometer setup. This introduces an additional optical path delay to the reflected probe beam while keeping the spatial coherence, which is easy to control.

Figure 5. The VISAR diagnostic: (a) schematic of a Mach–Zehnder interferometer setup in a typical VISAR system[Reference Celliers134] with two beamsplitters (BS1 and BS2), mirrors (M1 and M2) and a delay etalon inserted in one interferometer arm, the line-imaged data is recorded by a streak camera; (b) an example of typical VISAR data.
The velocity measurement is obtained from a fringe shift recorded by the streak camera during its sweep while the shock wave is moving. The fringe shift is a result of the Doppler shift caused by the moving shock front. When the shock surface moves the phase of the reflected light changes due to Doppler shift[Reference Takeda, Ina and Kobayashi133]. The phase-shifted signal will arrive through the shorter interferometer arm at time
![]() $t_{0}$
, while it will take
$t_{0}$
, while it will take
![]() $t=\unicode[STIX]{x1D70F}$
to pass through the longer arm. In the time between
$t=\unicode[STIX]{x1D70F}$
to pass through the longer arm. In the time between
![]() $t_{0}$
and
$t_{0}$
and
![]() $t_{0}+\unicode[STIX]{x1D70F}$
as the Doppler-shifted light arrives at the output beam splitter from the short arm and not yet the long arm, an increasing fringe shift will be observed, see Figure 5(a). After time
$t_{0}+\unicode[STIX]{x1D70F}$
as the Doppler-shifted light arrives at the output beam splitter from the short arm and not yet the long arm, an increasing fringe shift will be observed, see Figure 5(a). After time
![]() $\unicode[STIX]{x1D70F}$
passes, the signal from the longer arm fully catches up and no further fringe shifting is observed[Reference Takeda, Ina and Kobayashi133]. The shock velocity is then obtained from the total phase shift
$\unicode[STIX]{x1D70F}$
passes, the signal from the longer arm fully catches up and no further fringe shifting is observed[Reference Takeda, Ina and Kobayashi133]. The shock velocity is then obtained from the total phase shift
![]() $\unicode[STIX]{x0394}\unicode[STIX]{x1D719}$
as the interferometer sensitivity is known:
$\unicode[STIX]{x0394}\unicode[STIX]{x1D719}$
as the interferometer sensitivity is known:
![]() $U_{s}=\text{VPF}\times \unicode[STIX]{x0394}\unicode[STIX]{x1D719}/2\unicode[STIX]{x1D70B}$
, where
$U_{s}=\text{VPF}\times \unicode[STIX]{x0394}\unicode[STIX]{x1D719}/2\unicode[STIX]{x1D70B}$
, where
![]() $\text{VPF}=\unicode[STIX]{x1D706}/2\unicode[STIX]{x1D70F}$
is the velocity per fringe constant known for the specific system used[Reference Celliers134]. There is an intrinsic ambiguity in the VISAR measurement arising from the
$\text{VPF}=\unicode[STIX]{x1D706}/2\unicode[STIX]{x1D70F}$
is the velocity per fringe constant known for the specific system used[Reference Celliers134]. There is an intrinsic ambiguity in the VISAR measurement arising from the
![]() $2\unicode[STIX]{x1D70B}$
periodicity in the fringe interference. Only in very special cases of low shock velocity with respect to the VPF, the fringe shift can be traced using a single interferometer. Typically, the observed fringe shift is discontinuous. Thus, the current standard is to use two interferometers with different VPFs in a VISAR system to avoid ambiguity in the measurement[Reference Celliers134]. The phase shift is extracted from the raw VISAR data using a Fourier transform[Reference Takeda, Ina and Kobayashi133].
$2\unicode[STIX]{x1D70B}$
periodicity in the fringe interference. Only in very special cases of low shock velocity with respect to the VPF, the fringe shift can be traced using a single interferometer. Typically, the observed fringe shift is discontinuous. Thus, the current standard is to use two interferometers with different VPFs in a VISAR system to avoid ambiguity in the measurement[Reference Celliers134]. The phase shift is extracted from the raw VISAR data using a Fourier transform[Reference Takeda, Ina and Kobayashi133].
Additional thermodynamic properties of the shock can be extracted from the VISAR measurement using the Hugoniot relations derived from the mass, momentum and energy conservation across a single shock front[Reference Zel’dovich and Raizer57]:
where
![]() $\unicode[STIX]{x1D70C}_{0}$
and
$\unicode[STIX]{x1D70C}_{0}$
and
![]() $\unicode[STIX]{x1D70C}$
are initial and shock densities,
$\unicode[STIX]{x1D70C}$
are initial and shock densities,
![]() $P_{0}$
and
$P_{0}$
and
![]() $P$
are initial and shock pressures,
$P$
are initial and shock pressures,
![]() $E_{0}$
and
$E_{0}$
and
![]() $E$
are the initial and shock internal energies, while
$E$
are the initial and shock internal energies, while
![]() $U_{s}$
and
$U_{s}$
and
![]() $U_{p}$
refer to shock and particle velocities, respectively.
$U_{p}$
refer to shock and particle velocities, respectively.
![]() $U_{p}$
is the velocity of the material behind the shock, i.e., the piston that pushes the shockfront forward. From these equations, we obtain the relations
$U_{p}$
is the velocity of the material behind the shock, i.e., the piston that pushes the shockfront forward. From these equations, we obtain the relations
![]() $P=\unicode[STIX]{x1D70C}_{0}U_{s}U_{p}$
and
$P=\unicode[STIX]{x1D70C}_{0}U_{s}U_{p}$
and
![]() $\unicode[STIX]{x1D70C}=\unicode[STIX]{x1D70C}_{0}U_{s}/(U_{s}-U_{p})$
that can then be used to determine the pressure and density of the shocked material. The initial conditions are known, while
$\unicode[STIX]{x1D70C}=\unicode[STIX]{x1D70C}_{0}U_{s}/(U_{s}-U_{p})$
that can then be used to determine the pressure and density of the shocked material. The initial conditions are known, while
![]() $U_{s}$
is measured by VISAR.
$U_{s}$
is measured by VISAR.
![]() $U_{p}$
can be determined experimentally when the shock waves are driven by flyer plates, like those launched magnetically on the Z-machine in experiments by Knudson et al.
[Reference Knudson, Asay and Deeney60]. In these experiments the VISAR system measures both
$U_{p}$
can be determined experimentally when the shock waves are driven by flyer plates, like those launched magnetically on the Z-machine in experiments by Knudson et al.
[Reference Knudson, Asay and Deeney60]. In these experiments the VISAR system measures both
![]() $U_{s}$
and
$U_{s}$
and
![]() $U_{p}$
directly. A direct
$U_{p}$
directly. A direct
![]() $U_{p}$
measurement is possible in laser experiments for transparent pusher materials like quartz or with the help of transparent windows, e.g., LiF.
$U_{p}$
measurement is possible in laser experiments for transparent pusher materials like quartz or with the help of transparent windows, e.g., LiF.
Another standard technique to obtain
![]() $U_{p}$
is the impedance-matching (IM) method described in more detail in Refs. [Reference Zel’dovich and Raizer57, Reference Hicks69, Reference Celliers135]. This method is usually used in laser experiments, where
$U_{p}$
is the impedance-matching (IM) method described in more detail in Refs. [Reference Zel’dovich and Raizer57, Reference Hicks69, Reference Celliers135]. This method is usually used in laser experiments, where
![]() $U_{p}$
cannot be measured. A thick piston, also called pusher, is introduced into the planar target geometry sandwiched between the ablator and studied sample. For this purpose a standard pusher material (usually quartz or Al) with well known EOS, including the principal Hugoniot (i.e.,
$U_{p}$
cannot be measured. A thick piston, also called pusher, is introduced into the planar target geometry sandwiched between the ablator and studied sample. For this purpose a standard pusher material (usually quartz or Al) with well known EOS, including the principal Hugoniot (i.e.,
![]() $U_{s}-U_{p}$
relationship) and release curves must be used. IM can then provide
$U_{s}-U_{p}$
relationship) and release curves must be used. IM can then provide
![]() $U_{p}$
for a specific
$U_{p}$
for a specific
![]() $U_{s}$
at the point of shock breakout from the pusher standard into the sample material. In such experiments the reference (pusher) and sample impedances generally do not match, and the incident shock wave resolves into a transmitted shock and a reflected wave directed back into the standard material. Due to conservation of mass and momentum at the interface between the standard and the sample upon the passage of the shockfront through it, both materials maintain a common pressure and fluid velocity at this point and thus the sample
$U_{s}$
at the point of shock breakout from the pusher standard into the sample material. In such experiments the reference (pusher) and sample impedances generally do not match, and the incident shock wave resolves into a transmitted shock and a reflected wave directed back into the standard material. Due to conservation of mass and momentum at the interface between the standard and the sample upon the passage of the shockfront through it, both materials maintain a common pressure and fluid velocity at this point and thus the sample
![]() $U_{p}$
can be extracted from the Hugoniot relations[Reference Celliers135].
$U_{p}$
can be extracted from the Hugoniot relations[Reference Celliers135].
A thorough study of fluid deuterium compressed by a laser-driven shock at pressures between 45 and 220 GPa using the VISAR diagnostic was carried out by Hicks et al.
[Reference Hicks69]. A similar study was carried out by Knudson et al. using dynamic compression by a flyer plate launched by a z-pinch[Reference Knudson20, Reference Knudson81]. A remarkable measurement of shock-induced metallization of deuterium at
![]() ${\sim}50$
GPa was carried out by Celliers et al. with a continuous measurement of shock velocity and optical reflectance using the VISAR diagnostic[Reference Celliers19].
${\sim}50$
GPa was carried out by Celliers et al. with a continuous measurement of shock velocity and optical reflectance using the VISAR diagnostic[Reference Celliers19].
Optical pyrometry and streaked optical pyrometry (SOP), often used in conjunction with VISAR measurements for characterizing dense plasma shock waves, are generally considered to be a standard diagnostic for EOS measurements[Reference Falk136]. Plasma created by laser-driven shock will produce optical radiation which can be linked to the plasma temperature through the black body radiation relationship[Reference Zel’dovich and Raizer57]. The SOP data can be used to provide an accurate measurement of the temperatures of the shocked material which reach above 5000 K (
![]() ${\sim}0.4$
eV) by comparing the emission intensity from the shock front at a specific wavelength with the radiation distribution of a Planckian source. For this measurement the shock wave must be optically thick to visible light, so that the brightness temperature of the self-emission radiation approaches the temperature of the material making the black or grey body approximation valid for shock temperature measurement[Reference Zel’dovich and Raizer57].
${\sim}0.4$
eV) by comparing the emission intensity from the shock front at a specific wavelength with the radiation distribution of a Planckian source. For this measurement the shock wave must be optically thick to visible light, so that the brightness temperature of the self-emission radiation approaches the temperature of the material making the black or grey body approximation valid for shock temperature measurement[Reference Zel’dovich and Raizer57].
SOP consists of an imaging system with a well defined set of filters to pick a narrow wavelength band coupled to an optical streak camera providing a continuous record of the emission from the shock surface with great temporal and spatial resolution[Reference Miller137]. This instrument must be absolutely calibrated for measured optical radiation intensity such that emission temperature can be extracted from the streaked image. An example of such a system and calibration is provided by Miller et al. [Reference Miller137]. In case of optically transparent materials such as quartz, the self-emission from the shock front can be observed prior to the shock breakout at the back of the target. This is not possible with optically opaque materials. This is often solved by the use of a window made of a resilient material such as LiF that remains transparent up to 250 GPa and thus can provide a reliable temperature measurement during the shock breakout by keeping the back of the target at high density.
In most cases it is most appropriate to use the grey body distribution, which does not rely on the assumption that the shock is optically thick at all wavelengths as the black body distribution does. The reduced reflectivity of a grey body emitter increases the emissivity of the surface and thus changes the temperature measurement. The grey body radiates energy having the black body distribution reduced by a constant factor related to the reflectivity of its surface. According to Kirchhoff’s law of thermal radiation, the absorptivity and emissivity of a grey body are equal at any given temperature and wavelength and the black body distribution is thus reduced by a constant
![]() $(1-R)$
, where
$(1-R)$
, where
![]() $R$
denotes the reflectivity[Reference Zel’dovich and Raizer57, Reference Miller137]. The absolute reflectivity of the shocked material is usually obtained from simultaneous VISAR measurement. Calibration with quartz pushers for the absolute temperature determination is now also common[Reference Falk136, Reference Hicks138]. The process of reducing the temperature measurement for a SOP trace as well as the calibration process of the instrument is described in detail in Refs. [Reference Miller137, Reference Gregor139]. Similar methods have proven to be reliable temperature diagnostics for shock-compressed deuterium at conditions relevant to the interiors of Jovian planets[Reference Collins140, Reference Bailey141].
$R$
denotes the reflectivity[Reference Zel’dovich and Raizer57, Reference Miller137]. The absolute reflectivity of the shocked material is usually obtained from simultaneous VISAR measurement. Calibration with quartz pushers for the absolute temperature determination is now also common[Reference Falk136, Reference Hicks138]. The process of reducing the temperature measurement for a SOP trace as well as the calibration process of the instrument is described in detail in Refs. [Reference Miller137, Reference Gregor139]. Similar methods have proven to be reliable temperature diagnostics for shock-compressed deuterium at conditions relevant to the interiors of Jovian planets[Reference Collins140, Reference Bailey141].
Both of these diagnostics can also be used for shock break-out timing measurements to determine shock velocity using stepped targets[Reference Falk142]. Phase transformations of MgO form B1 to B2 crystal structures above 360 GPa and metallization above 600 GPa during laser-driven shock compression to pressures reaching maximum of 1400 GPa were observed by McWilliams et al. [Reference McWilliams39]. A combination of VISAR and SOP diagnostics was utilized to characterize the MgO state during the dynamic compression. The observed phase transitions exhibited large latent heats which are likely to affect the structure and evolution of super-Earths. These results also lead to the conclusion that magmas deep inside terrestrial planets can be electrically conductive, which has significant impact on the magnetic dynamo function inside these planets[Reference McWilliams39]. The main disadvantage of using such optical systems is the fact that they only measure surface conditions, but are unable to probe through the bulk of the material that can be subjected to significant gradients in temperature and density, which can only be probed by active probes capable of penetrating through the dense material such as X-rays as shown by Falk et al. [Reference Falk143].
3.2.2 X-ray Thomson scattering
X-ray Thomson scattering (XRTS) has recently shown a great potential to study WDM[Reference Glenzer and Redmer144]. This diagnostic was pioneered by Glenzer et al.
[Reference Glenzer53, Reference Glenzer110]. The first angularly resolved elastic scattering measurement was carried out by Riley et al.
[Reference Riley145]. The first spectrally resolved measurements of collective and noncollective XRTS from isochorically heated Be were reported by Glenzer et al.
[Reference Glenzer53, Reference Glenzer110]. The fluctuation–dissipation theorem links the dynamic structure factor
![]() $S(k,\unicode[STIX]{x1D714})$
, which describes the shape of the scattering spectrum, to the dielectric function and through it gives access to the thermodynamic properties (temperature and density) of the system, allowing calculations of the electric conductivity, pressure and entropy of astrophysically relevant plasmas[Reference Gregori146]. The use of XRTS for temperature measurements in particular provides a more reliable measurement than the SOP diagnostic, which only detects surface brightness temperature.
$S(k,\unicode[STIX]{x1D714})$
, which describes the shape of the scattering spectrum, to the dielectric function and through it gives access to the thermodynamic properties (temperature and density) of the system, allowing calculations of the electric conductivity, pressure and entropy of astrophysically relevant plasmas[Reference Gregori146]. The use of XRTS for temperature measurements in particular provides a more reliable measurement than the SOP diagnostic, which only detects surface brightness temperature.
Within the Chihara formalism
![]() $S(k,\unicode[STIX]{x1D714})$
is given in the form shown in Equation (5)[Reference Glenzer and Redmer144, Reference Gregori146], where
$S(k,\unicode[STIX]{x1D714})$
is given in the form shown in Equation (5)[Reference Glenzer and Redmer144, Reference Gregori146], where
![]() $\unicode[STIX]{x1D714}$
is the frequency of the scattered radiation and the scattering wavevector
$\unicode[STIX]{x1D714}$
is the frequency of the scattered radiation and the scattering wavevector
![]() $k=(4\unicode[STIX]{x1D70B}/\unicode[STIX]{x1D706}_{0})\sin (\unicode[STIX]{x1D703}/2)$
is defined as the difference between the wavevectors of the incident and scattered electromagnetic waves. Here
$k=(4\unicode[STIX]{x1D70B}/\unicode[STIX]{x1D706}_{0})\sin (\unicode[STIX]{x1D703}/2)$
is defined as the difference between the wavevectors of the incident and scattered electromagnetic waves. Here
![]() $\unicode[STIX]{x1D706}_{0}$
is the wavelength of the incident wave and
$\unicode[STIX]{x1D706}_{0}$
is the wavelength of the incident wave and
![]() $\unicode[STIX]{x1D703}$
is the scattering angle, see Figure 6(a).
$\unicode[STIX]{x1D703}$
is the scattering angle, see Figure 6(a).
 $$\begin{eqnarray}\displaystyle S(k,\unicode[STIX]{x1D714}) & = & \displaystyle |f_{I}(k)+q(k)|^{2}S_{ii}(k,\unicode[STIX]{x1D714})+Z_{f}S_{ee}^{0}(k,\unicode[STIX]{x1D714})\nonumber\\ \displaystyle & & \displaystyle +\,Z_{c}\int \tilde{S}_{ce}(k,\unicode[STIX]{x1D714}-\unicode[STIX]{x1D714}^{\prime })S_{s}(k,\unicode[STIX]{x1D714}^{\prime })\,\text{d}\unicode[STIX]{x1D714}^{\prime }.\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle S(k,\unicode[STIX]{x1D714}) & = & \displaystyle |f_{I}(k)+q(k)|^{2}S_{ii}(k,\unicode[STIX]{x1D714})+Z_{f}S_{ee}^{0}(k,\unicode[STIX]{x1D714})\nonumber\\ \displaystyle & & \displaystyle +\,Z_{c}\int \tilde{S}_{ce}(k,\unicode[STIX]{x1D714}-\unicode[STIX]{x1D714}^{\prime })S_{s}(k,\unicode[STIX]{x1D714}^{\prime })\,\text{d}\unicode[STIX]{x1D714}^{\prime }.\end{eqnarray}$$
The first term in Equation (5) represents the electrons whose motion is strongly correlated with the ions, and thus this term relates to the ion–ion structure factor
![]() $S_{ii}(k,\unicode[STIX]{x1D714})$
. The ion form factor
$S_{ii}(k,\unicode[STIX]{x1D714})$
. The ion form factor
![]() $f_{I}(k)$
and the screening term
$f_{I}(k)$
and the screening term
![]() $q(k)$
describe the distribution of the electrons tightly bound to the nuclei and the free and valence electrons. The second term models the free electrons that do not follow the ion motion producing inelastic scattering due to the Compton effect.
$q(k)$
describe the distribution of the electrons tightly bound to the nuclei and the free and valence electrons. The second term models the free electrons that do not follow the ion motion producing inelastic scattering due to the Compton effect.
![]() $S_{ee}(k,\unicode[STIX]{x1D714})$
is the high frequency part of the electron–electron correlation function. The last term in the above expression includes the contribution of the inelastic scattering due to bound-free transitions of the core electrons. Here
$S_{ee}(k,\unicode[STIX]{x1D714})$
is the high frequency part of the electron–electron correlation function. The last term in the above expression includes the contribution of the inelastic scattering due to bound-free transitions of the core electrons. Here
![]() $Z_{c}$
denotes the number of bound electrons, hence
$Z_{c}$
denotes the number of bound electrons, hence
![]() $Z_{f}+Z_{c}=Z$
corresponds to the atomic number of the neutral atom.
$Z_{f}+Z_{c}=Z$
corresponds to the atomic number of the neutral atom.
![]() $S_{ce}(k,\unicode[STIX]{x1D714})$
is the dynamic structure factor of the core electrons undergoing Raman transitions to the continuum.
$S_{ce}(k,\unicode[STIX]{x1D714})$
is the dynamic structure factor of the core electrons undergoing Raman transitions to the continuum.
![]() $S_{s}(k,\unicode[STIX]{x1D714})$
is the dynamic structure factor of a single ion, which modulates the contribution of the inelastic processes by the self-motion of the ions.
$S_{s}(k,\unicode[STIX]{x1D714})$
is the dynamic structure factor of a single ion, which modulates the contribution of the inelastic processes by the self-motion of the ions.

Figure 6. (a) Schematic of the X-ray Thomson scattering process. XRTS spectra from warm dense deuterium compressed by laser-driven shock obtained by Davis et al. [Reference Davis158]: these measurements were carried out both (b) in collective geometry showing the downshifted-plasmon feature and (c) in noncollective/backscattering geometry with a very clear Compton peak.
Depending on the geometry of the experiment and energy of the probe two different regimes can be accessed. These are defined by the value of the scattering parameter
![]() $\unicode[STIX]{x1D6FC}=1/k\unicode[STIX]{x1D706}_{s}$
, which is the ratio of the scattering scale length and the plasma screening length
$\unicode[STIX]{x1D6FC}=1/k\unicode[STIX]{x1D706}_{s}$
, which is the ratio of the scattering scale length and the plasma screening length
![]() $\unicode[STIX]{x1D706}_{s}$
. For classical low density plasma the screening length, over which a Coulomb field of a test particle is shielded by the charges surrounding it, is the Debye length
$\unicode[STIX]{x1D706}_{s}$
. For classical low density plasma the screening length, over which a Coulomb field of a test particle is shielded by the charges surrounding it, is the Debye length
![]() $\unicode[STIX]{x1D706}_{D}=\sqrt{\unicode[STIX]{x1D700}_{0}k_{B}T_{e}/e^{2}n_{e}}$
, where
$\unicode[STIX]{x1D706}_{D}=\sqrt{\unicode[STIX]{x1D700}_{0}k_{B}T_{e}/e^{2}n_{e}}$
, where
![]() $k_{B}$
stands for the Boltzmann constant and
$k_{B}$
stands for the Boltzmann constant and
![]() $T_{e}$
is the electron temperature[Reference Glenzer and Redmer144]. In a highly degenerate state
$T_{e}$
is the electron temperature[Reference Glenzer and Redmer144]. In a highly degenerate state
![]() $\unicode[STIX]{x1D706}_{s}$
is given by the Thomas–Fermi length
$\unicode[STIX]{x1D706}_{s}$
is given by the Thomas–Fermi length
![]() $\unicode[STIX]{x1D706}_{\mathit{TF}}=\sqrt{2\unicode[STIX]{x1D700}_{0}E_{F}/3n_{e}e^{2}}$
, which depends only on electron density
$\unicode[STIX]{x1D706}_{\mathit{TF}}=\sqrt{2\unicode[STIX]{x1D700}_{0}E_{F}/3n_{e}e^{2}}$
, which depends only on electron density
![]() $n_{e}$
[Reference Glenzer and Redmer144]. To account for partial degeneracy of the electron gas, the inverse of the screening length
$n_{e}$
[Reference Glenzer and Redmer144]. To account for partial degeneracy of the electron gas, the inverse of the screening length
![]() $\unicode[STIX]{x1D705}_{e}=1/\unicode[STIX]{x1D706}_{s}$
should be calculated as
$\unicode[STIX]{x1D705}_{e}=1/\unicode[STIX]{x1D706}_{s}$
should be calculated as
![]() $\unicode[STIX]{x1D705}_{e}^{2}=(4e^{2}m_{e})/(\unicode[STIX]{x1D70B}\hbar ^{3})\int f_{e}(p)\,\text{d}p$
, where
$\unicode[STIX]{x1D705}_{e}^{2}=(4e^{2}m_{e})/(\unicode[STIX]{x1D70B}\hbar ^{3})\int f_{e}(p)\,\text{d}p$
, where
![]() $f_{e}(p)$
is the Fermi distribution[Reference Gericke, Vorberger, Wünsch and Gregori147]. It is more practical to use the Debye form with an effective temperature[Reference Dharma-wardana and Perrot148, Reference Perrot149]:
$f_{e}(p)$
is the Fermi distribution[Reference Gericke, Vorberger, Wünsch and Gregori147]. It is more practical to use the Debye form with an effective temperature[Reference Dharma-wardana and Perrot148, Reference Perrot149]:
 $$\begin{eqnarray}\displaystyle & & \displaystyle \unicode[STIX]{x1D705}_{e}=\frac{1}{\unicode[STIX]{x1D706}_{s}}=\sqrt{\frac{4\unicode[STIX]{x1D70B}e^{2}n_{e}}{k_{B}T_{e}^{eff}}}\nonumber\\ \displaystyle & & \displaystyle \quad \text{with}\quad T_{e}^{eff}=(T_{e}^{4}+T_{F}^{4})^{1/4},\hspace{40.00006pt}\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle \unicode[STIX]{x1D705}_{e}=\frac{1}{\unicode[STIX]{x1D706}_{s}}=\sqrt{\frac{4\unicode[STIX]{x1D70B}e^{2}n_{e}}{k_{B}T_{e}^{eff}}}\nonumber\\ \displaystyle & & \displaystyle \quad \text{with}\quad T_{e}^{eff}=(T_{e}^{4}+T_{F}^{4})^{1/4},\hspace{40.00006pt}\end{eqnarray}$$
which interpolates between the Debye and Thomas–Fermi screening length and yields results with less than 2% error for all densities[Reference Gericke, Vorberger, Wünsch and Gregori147].
For
![]() $\unicode[STIX]{x1D6FC}>1$
, we are dealing with collective scattering when X-rays scatter inelastically from collective motion in the plasma, i.e., the plasmon waves. This creates upshifted- and downshifted-plasmon features located at plasma frequency away from the probe line and the measurement is highly sensitive to the electron density. By measuring both the plasmon dispersion and width with
$\unicode[STIX]{x1D6FC}>1$
, we are dealing with collective scattering when X-rays scatter inelastically from collective motion in the plasma, i.e., the plasmon waves. This creates upshifted- and downshifted-plasmon features located at plasma frequency away from the probe line and the measurement is highly sensitive to the electron density. By measuring both the plasmon dispersion and width with
![]() ${\sim}1$
eV resolution, it is possible to distinguish between different theoretical models and hence precisely determine the collision rate and the local field effects in the electron species[Reference Gregori146]. In the case of noncollective scattering with
${\sim}1$
eV resolution, it is possible to distinguish between different theoretical models and hence precisely determine the collision rate and the local field effects in the electron species[Reference Gregori146]. In the case of noncollective scattering with
![]() $\unicode[STIX]{x1D6FC}<1$
, the X-rays scatter from the individual electrons that undergo thermal motion and thus provide us with a measurement of the electron temperature in the bulk plasma and can even detect temperature gradients if spatial resolution is available[Reference Falk52]. Electron temperature can also be accurately determined from the detailed balance, i.e., intensity ratio of the upshifted- and downshifted-plasmon peaks in the collective regime. The ratio of the elastic and inelastic peaks gives the ionization state. The inelastic scattering spectral shapes can also provide information about the bound-free transitions. Figure 6(a) shows the schematic model of XRTS and experimental examples of scattering spectra both in collective and noncollective regimes. Thus XRTS is very sensitive to the thermodynamic conditions, microscopic structure and the concentration of atomic species in the studied WDM samples and these quantities can be extracted from measured XRTS spectra by comparing them with analytical fits[Reference Gregori146, Reference Chapman150–Reference Starrett and Saumon152].
$\unicode[STIX]{x1D6FC}<1$
, the X-rays scatter from the individual electrons that undergo thermal motion and thus provide us with a measurement of the electron temperature in the bulk plasma and can even detect temperature gradients if spatial resolution is available[Reference Falk52]. Electron temperature can also be accurately determined from the detailed balance, i.e., intensity ratio of the upshifted- and downshifted-plasmon peaks in the collective regime. The ratio of the elastic and inelastic peaks gives the ionization state. The inelastic scattering spectral shapes can also provide information about the bound-free transitions. Figure 6(a) shows the schematic model of XRTS and experimental examples of scattering spectra both in collective and noncollective regimes. Thus XRTS is very sensitive to the thermodynamic conditions, microscopic structure and the concentration of atomic species in the studied WDM samples and these quantities can be extracted from measured XRTS spectra by comparing them with analytical fits[Reference Gregori146, Reference Chapman150–Reference Starrett and Saumon152].
Since the Thomson cross section is very low, the XRTS process produces rather weak signals which put significant restrictions on the experimental setups. The X-ray probes must be very bright with at least
![]() $10^{12}$
photons on target for a single shot measurement[Reference Glenzer and Redmer144]. Closely packed geometries, good shielding, efficient spectrometers and detectors are crucial for this measurement. Most commonly used X-ray sources are laser-generated He-
$10^{12}$
photons on target for a single shot measurement[Reference Glenzer and Redmer144]. Closely packed geometries, good shielding, efficient spectrometers and detectors are crucial for this measurement. Most commonly used X-ray sources are laser-generated He-
![]() $\unicode[STIX]{x03B1}$
or Ly-
$\unicode[STIX]{x03B1}$
or Ly-
![]() $\unicode[STIX]{x03B1}$
sources emission (at several keV), which provide sufficiently narrow line profile and high enough energy for most experimental requirements while the conversion efficiencies are relatively high reaching
$\unicode[STIX]{x03B1}$
sources emission (at several keV), which provide sufficiently narrow line profile and high enough energy for most experimental requirements while the conversion efficiencies are relatively high reaching
![]() ${\sim}1\%$
[Reference Fournier153]. The main disadvantage of these hydrogen- or helium-like sources is their wide spectral profile and multiple spectral features (they are doublets often with multiple resonance and satellite lines), which significantly decreases the spectral resolution of the XRTS measurement. Ti or Mo He-
${\sim}1\%$
[Reference Fournier153]. The main disadvantage of these hydrogen- or helium-like sources is their wide spectral profile and multiple spectral features (they are doublets often with multiple resonance and satellite lines), which significantly decreases the spectral resolution of the XRTS measurement. Ti or Mo He-
![]() $\unicode[STIX]{x03B1}$
and Cl Ly-
$\unicode[STIX]{x03B1}$
and Cl Ly-
![]() $\unicode[STIX]{x03B1}$
sources were used in many of the first laser XRTS experiments to study the thermodynamic properties, equation of state and ionic structure of WDM[Reference Glenzer53, Reference Glenzer110, Reference Gregori112, Reference García Saiz154–Reference Ma156]. The first XRTS measurement of temperature and density of deuterium at conditions relevant to the interior of Jovian planets was carried out by Regan et al.
[Reference Regan157]. The first measurement of dissociation-induced metallization of shock-compressed deuterium with a combination of collective and noncollective XRTS in conjunction with the VISAR diagnostic was carried out by Davis et al.
[Reference Davis158], also shown in Figures 6(b) and 6(c). This was a significant result, where multiple diagnostics were compared with DFT-MD simulations in order to calculate optical reflectivity and dynamic conductivity and determine conditions under which hydrogen becomes metallic and thus capable of driving magnetic dynamos of planets like Jupiter[Reference Davis158].
$\unicode[STIX]{x03B1}$
sources were used in many of the first laser XRTS experiments to study the thermodynamic properties, equation of state and ionic structure of WDM[Reference Glenzer53, Reference Glenzer110, Reference Gregori112, Reference García Saiz154–Reference Ma156]. The first XRTS measurement of temperature and density of deuterium at conditions relevant to the interior of Jovian planets was carried out by Regan et al.
[Reference Regan157]. The first measurement of dissociation-induced metallization of shock-compressed deuterium with a combination of collective and noncollective XRTS in conjunction with the VISAR diagnostic was carried out by Davis et al.
[Reference Davis158], also shown in Figures 6(b) and 6(c). This was a significant result, where multiple diagnostics were compared with DFT-MD simulations in order to calculate optical reflectivity and dynamic conductivity and determine conditions under which hydrogen becomes metallic and thus capable of driving magnetic dynamos of planets like Jupiter[Reference Davis158].
The laser-driven K-
![]() $\unicode[STIX]{x03B1}$
emission has around an order of magnitude lower conversion efficiency than conventional He-
$\unicode[STIX]{x03B1}$
emission has around an order of magnitude lower conversion efficiency than conventional He-
![]() $\unicode[STIX]{x03B1}$
, but has the advantage of shorter duration, i.e., better temporal resolution and narrow line profile[Reference Glenzer and Redmer144]. Probes with short duration on the level of tens of to hundreds of fs are capable of accessing nonequilibrium dynamics and obtaining information on dynamic processes such as transport coefficients. Ultrafast XRTS measurement of LiH targets compressed by a 0.45 kJ shaped laser pulse with 6 ns was obtained by Kritcher et al.
[Reference Kritcher51]. A laser-driven Ti K-
$\unicode[STIX]{x03B1}$
, but has the advantage of shorter duration, i.e., better temporal resolution and narrow line profile[Reference Glenzer and Redmer144]. Probes with short duration on the level of tens of to hundreds of fs are capable of accessing nonequilibrium dynamics and obtaining information on dynamic processes such as transport coefficients. Ultrafast XRTS measurement of LiH targets compressed by a 0.45 kJ shaped laser pulse with 6 ns was obtained by Kritcher et al.
[Reference Kritcher51]. A laser-driven Ti K-
![]() $\unicode[STIX]{x03B1}$
source with duration of 5 ps was used to measure evolution and coalescence of two shocks with 10 ps temporal resolution and transition to a metallic dense plasma state relevant to conditions of planetary formation. It is expected that lines K-
$\unicode[STIX]{x03B1}$
source with duration of 5 ps was used to measure evolution and coalescence of two shocks with 10 ps temporal resolution and transition to a metallic dense plasma state relevant to conditions of planetary formation. It is expected that lines K-
![]() $\unicode[STIX]{x03B1}$
yield can be enhanced, possibly by a whole order of magnitude, thanks to the strong electric fields created in the cavities within the nanostructured target that allow more fast electrons to move through the target and create inner-shell emission at higher intensity[Reference Ovchinnikov159]. However, kJ short-pulse class lasers are at the very frontier of what the current state of technology can provide and there are very few systems with such capabilities. An alternative route to ultrafast XRTS is provided by new tunable X-ray free electron lasers like LCLS, SACLA or the European X-FEL, which are able to provide
$\unicode[STIX]{x03B1}$
yield can be enhanced, possibly by a whole order of magnitude, thanks to the strong electric fields created in the cavities within the nanostructured target that allow more fast electrons to move through the target and create inner-shell emission at higher intensity[Reference Ovchinnikov159]. However, kJ short-pulse class lasers are at the very frontier of what the current state of technology can provide and there are very few systems with such capabilities. An alternative route to ultrafast XRTS is provided by new tunable X-ray free electron lasers like LCLS, SACLA or the European X-FEL, which are able to provide
![]() $10^{12}$
photons with a very narrow spectral profile for a very precise XRTS measurement. The first XRTS measurement of warm dense hydrogen was carried out by Fäustlin et al. at the FLASH facility in Hamburg with a soft X-ray beam at 91.8 eV in a classical pump-and-probe setup, where the cryogenic hydrogen jet was heated and probed by the same beam and collective XRTS spectrum was used to measure the electron density and temperature with femtosecond temporal resolution[Reference Fäustlin108]. This experiment highlighted the difficulties associated with understanding of the nonequilibrium dynamical systems and related issues with the classical description of XRTS[Reference Chapman150]. More recently, the LCLS facility has been used to obtain high precision XRTS data of WDM such as the experiment carried out by Fletcher et al. on Al compressed by a laser-driven shock wave[Reference Fletcher160].
$10^{12}$
photons with a very narrow spectral profile for a very precise XRTS measurement. The first XRTS measurement of warm dense hydrogen was carried out by Fäustlin et al. at the FLASH facility in Hamburg with a soft X-ray beam at 91.8 eV in a classical pump-and-probe setup, where the cryogenic hydrogen jet was heated and probed by the same beam and collective XRTS spectrum was used to measure the electron density and temperature with femtosecond temporal resolution[Reference Fäustlin108]. This experiment highlighted the difficulties associated with understanding of the nonequilibrium dynamical systems and related issues with the classical description of XRTS[Reference Chapman150]. More recently, the LCLS facility has been used to obtain high precision XRTS data of WDM such as the experiment carried out by Fletcher et al. on Al compressed by a laser-driven shock wave[Reference Fletcher160].
3.2.3 X-ray radiography
A typical radiography system consists of a separate X-ray backlighter target back-illuminating the studied WDM sample. The standard technique of area backlighting with targets heated by a laser pulse is usually used to radiograph objects of comparable size to the backlighter target. In this case a pinhole is used as an imaging element. This becomes challenging at the higher X-ray energies needed to probe WDM as most facilities do not have sufficient laser energy to produce a large and uniform area of X-ray emission. Thus point projection X-ray sources driven by high energy lasers have become a more suitable option for radiography in WDM experiments. A great example of a X-ray radiography platform is the pinhole-apertured point backlighter (PAPBL) geometry[Reference Workman161]. Figure 7 shows data obtained using this platform. This is the most common setup used in the point projection radiography, where the 4
![]() $\unicode[STIX]{x1D70B}$
X-ray source is restricted by a small pinhole and the spatial resolution of the radiograph is determined by the distance from the source to the target and detector. Tightly focused laser beams can provide high enough laser irradiance to produce higher plasma temperatures and thus brighter, more energetic X-ray emission. In addition such sources create a more uniform X-ray emitting area. Large area backlighters can be used if sufficient energy is available. The big area backlighter (BABL) was developed at the National Ignition Facility as a viable backlighter for HED experiments[Reference Flippo162]. Flippo et al. have demonstrated laser-to-X-ray conversion efficiencies of up to 5% for various backlighter materials including Zn, Fe, V and Cu producing bright He-
$\unicode[STIX]{x1D70B}$
X-ray source is restricted by a small pinhole and the spatial resolution of the radiograph is determined by the distance from the source to the target and detector. Tightly focused laser beams can provide high enough laser irradiance to produce higher plasma temperatures and thus brighter, more energetic X-ray emission. In addition such sources create a more uniform X-ray emitting area. Large area backlighters can be used if sufficient energy is available. The big area backlighter (BABL) was developed at the National Ignition Facility as a viable backlighter for HED experiments[Reference Flippo162]. Flippo et al. have demonstrated laser-to-X-ray conversion efficiencies of up to 5% for various backlighter materials including Zn, Fe, V and Cu producing bright He-
![]() $\unicode[STIX]{x03B1}$
line emission with
$\unicode[STIX]{x03B1}$
line emission with
![]() $\gg 100$
kJ incident laser energy.
$\gg 100$
kJ incident laser energy.
Similarly to the development of the XRTS diagnostic, the X-ray sources suitable for X-ray radiography have gone through a long evolution. The first radiographs of dense plasmas with primary ICF application were obtained with He-
![]() $\unicode[STIX]{x03B1}$
X-ray emission for laser-heated plasma[Reference Benuzzi-Mounaix163, Reference Hicks164]. Since then, significant effort was made to increase the X-ray energy, temporal and spatial resolution. Improved temporal resolution of hard X-ray radiography was achieved by K-
$\unicode[STIX]{x03B1}$
X-ray emission for laser-heated plasma[Reference Benuzzi-Mounaix163, Reference Hicks164]. Since then, significant effort was made to increase the X-ray energy, temporal and spatial resolution. Improved temporal resolution of hard X-ray radiography was achieved by K-
![]() $\unicode[STIX]{x03B1}$
sources driven by short-pulse lasers[Reference Ravasio165–Reference Brambrink169]. Pioneering work was carried out by Park et al. in the development of bright ultrafast high energy (up to 75 keV) K-
$\unicode[STIX]{x03B1}$
sources driven by short-pulse lasers[Reference Ravasio165–Reference Brambrink169]. Pioneering work was carried out by Park et al. in the development of bright ultrafast high energy (up to 75 keV) K-
![]() $\unicode[STIX]{x03B1}$
sources based on fluorescence of hot electrons accelerated by a short-pulse laser for X-ray radiography applications, but also in utilizing spherically bent imaging crystals for high spatial resolution measurements at these extreme X-ray energies[Reference Park170, Reference Park171]. The Bremsstrahlung radiation for high areal density object radiography has been extended into the MeV region with intense short (
$\unicode[STIX]{x03B1}$
sources based on fluorescence of hot electrons accelerated by a short-pulse laser for X-ray radiography applications, but also in utilizing spherically bent imaging crystals for high spatial resolution measurements at these extreme X-ray energies[Reference Park170, Reference Park171]. The Bremsstrahlung radiation for high areal density object radiography has been extended into the MeV region with intense short (
![]() ${<}10$
ps) pulse lasers. These are particularly useful for the study of high-
${<}10$
ps) pulse lasers. These are particularly useful for the study of high-
![]() $Z$
materials such as gold or copper where classical K-
$Z$
materials such as gold or copper where classical K-
![]() $\unicode[STIX]{x03B1}$
backlighters would not have sufficient brightness or energy[Reference Courtois172, Reference Westover173]. An alternative approach to X-ray radiography using broadband x-pinch sources based on pulsed-power technology has also been utilized primarily at z-pinch facilities[Reference Shelkovenko, Pikuz and Hammer174].
$\unicode[STIX]{x03B1}$
backlighters would not have sufficient brightness or energy[Reference Courtois172, Reference Westover173]. An alternative approach to X-ray radiography using broadband x-pinch sources based on pulsed-power technology has also been utilized primarily at z-pinch facilities[Reference Shelkovenko, Pikuz and Hammer174].

Figure 7. An example of X-ray radiographic measurement on warm dense carbon carried out by Falk et al.
[Reference Falk52, Reference Falk142]. A diamond sample was driven by laser with
![]() $5\times 10^{14}~\text{W/cm}^{2}$
intensity. A point projection radiography setup with 30
$5\times 10^{14}~\text{W/cm}^{2}$
intensity. A point projection radiography setup with 30
![]() $\unicode[STIX]{x03BC}$
m pinhole and Vanadium He-
$\unicode[STIX]{x03BC}$
m pinhole and Vanadium He-
![]() $\unicode[STIX]{x03B1}$
backlighter at 5.2 keV were used. (a) An example of the X-ray film used for the radiographic measurement, (b) model of the target layout including the Ni He-
$\unicode[STIX]{x03B1}$
backlighter at 5.2 keV were used. (a) An example of the X-ray film used for the radiographic measurement, (b) model of the target layout including the Ni He-
![]() $\unicode[STIX]{x03B1}$
backlighter and pinhole used for XRTS measurement as viewed by the radiography film, (c) detail of the radiographic measurement including the CH step wedge used for X-ray intensity calibration, and (d) Abel inversion plot used to extract the density from shock-released diamond.
$\unicode[STIX]{x03B1}$
backlighter and pinhole used for XRTS measurement as viewed by the radiography film, (c) detail of the radiographic measurement including the CH step wedge used for X-ray intensity calibration, and (d) Abel inversion plot used to extract the density from shock-released diamond.
X-ray radiography can be used to determine the density of the WDM sample if the opacity is well known or can also be used for opacity measurements. Point projection X-ray radiography was used to obtain an independent measurement of density of shock-compressed boron using Fe K-
![]() $\unicode[STIX]{x03B1}$
source at 6.4 keV by Le Pape et al.
[Reference Le Pape175]. The use of the short-pulse probe allowed excellent temporal resolution of 100 ps improving the resolution of the experiment and reducing the smearing of the radiographic image during the shock wave propagation. This measurement was then constrained by density measurements from collective XRTS. For extraction of information about the density of WDM using X-ray radiography assumptions about cold opacity or the use of reliable opacity measurements or tables must be made[Reference Falk142].
$\unicode[STIX]{x03B1}$
source at 6.4 keV by Le Pape et al.
[Reference Le Pape175]. The use of the short-pulse probe allowed excellent temporal resolution of 100 ps improving the resolution of the experiment and reducing the smearing of the radiographic image during the shock wave propagation. This measurement was then constrained by density measurements from collective XRTS. For extraction of information about the density of WDM using X-ray radiography assumptions about cold opacity or the use of reliable opacity measurements or tables must be made[Reference Falk142].
Since each diagnostic has some limitations, there has been a major move towards combinations of various diagnostic systems to obtain fully experimentally determined EOS measurements that do not require any additional modelling or theoretical assumptions. Combination of X-ray radiography with XRTS was done by Le Pape et al. [Reference Le Pape175]. The first fully model-independent EOS measurement was obtained by Falk et al. on shock-released carbon using a combination of noncollective XRTS yielding temperature, X-ray radiography providing an independent density measurement, and VISAR as well as SOP diagnostics that determined the pressure based on experimentally verified relationship between shock velocity and release pressure in a low density silica aerogel foam[Reference Falk52, Reference Falk142].
3.2.4 X-ray absorption spectroscopy
Another key WDM diagnostic is X-ray absorption spectroscopy, which similarly to XRTS and X-ray radiography has an advantage over the optical probes as X-rays are capable of penetrating deep inside WDM and thus provide bulk, not just surface measurements of the samples. Since the early beginnings of X-ray physics, edges in X-ray absorption spectra have been used to study and identify materials and their structure. In particular the study of the K-edge defined by the binding of K-shell electrons is very important for WDM as the energetic position and shape of this edge are not fixed, but heavily dependent on the thermodynamic conditions and bonding in the matter. These changes in the K-edge depend on three main factors: continuum lowering, shifts due to ionization and electron degeneracy[Reference Stewart and Pyatt176]. Continuum lowering or ionization potential depression tends to shift the edge position to a lower energy as the energy levels of bound electrons are raised by interaction with electric fields of the surrounding plasma. Ionization of heated dense plasmas tends to move the K-edge position to a higher energy. Finally, Pauli blocking in highly degenerate plasmas can cause shifts in the effective edge position in both directions depending on the thermodynamic conditions. This effect was first observed by Bradley et al. [Reference Bradley177].
A very robust X-ray absorption spectroscopic approach to study multiple properties of WDM is offered by XANES (X-absorption near edge structure) or EXAFS (extended X-ray absorption fine structure) methods[Reference Dorchies and Recoules178]. The boundary between these two regions lies
![]() ${\sim}30$
–50 eV above the K-edge. Publications focused on WDM usually use the XANES term for description of the whole spectra including the edge. During the absorption process the X-rays from the incoming probe beam photoionize the electrons which get ejected into the continuum state with very low residual energy. Here they undergo scattering by surrounding ions. This generates quantum mechanical interference of the scattered waves and causes oscillations in the final state amplitude that leads to structure in the absorption spectrum, see Figure 8. Thus, this structure in the absorption spectra provides information about the ionic structure of matter and studies processes like solid to liquid transition as shown by Leguay et al.
[Reference Leguay179]. Density can also be determined from the position of the ion–ion correlation peaks. These oscillations depend on the ion correlations, which in turn depend on temperature. The depth of these oscillations is thus temperature dependent and these features smooth out at higher temperatures. Ionization state and thus temperature of the plasma can also be determined from the shifts in these structures. Depending on the conditions and
${\sim}30$
–50 eV above the K-edge. Publications focused on WDM usually use the XANES term for description of the whole spectra including the edge. During the absorption process the X-rays from the incoming probe beam photoionize the electrons which get ejected into the continuum state with very low residual energy. Here they undergo scattering by surrounding ions. This generates quantum mechanical interference of the scattered waves and causes oscillations in the final state amplitude that leads to structure in the absorption spectrum, see Figure 8. Thus, this structure in the absorption spectra provides information about the ionic structure of matter and studies processes like solid to liquid transition as shown by Leguay et al.
[Reference Leguay179]. Density can also be determined from the position of the ion–ion correlation peaks. These oscillations depend on the ion correlations, which in turn depend on temperature. The depth of these oscillations is thus temperature dependent and these features smooth out at higher temperatures. Ionization state and thus temperature of the plasma can also be determined from the shifts in these structures. Depending on the conditions and
![]() $Z$
of the sample it may be favourable to study the K- or L-edge. For higher
$Z$
of the sample it may be favourable to study the K- or L-edge. For higher
![]() $Z$
, higher temperatures are needed to ionize the K-shell. The shift and slope of the edge can provide information about plasma temperature. As the photons are absorbed via the photoionization the shape of the edge explores the electronic density of states of the outer electrons. With increasing temperature the slope of the edge becomes less steep. This effect is sometimes referred to as the edge broadening as seen by Lévy et al.
[Reference Lévy180]. Thus the shift of the edge is a combined effect of plasma temperature and density.
$Z$
, higher temperatures are needed to ionize the K-shell. The shift and slope of the edge can provide information about plasma temperature. As the photons are absorbed via the photoionization the shape of the edge explores the electronic density of states of the outer electrons. With increasing temperature the slope of the edge becomes less steep. This effect is sometimes referred to as the edge broadening as seen by Lévy et al.
[Reference Lévy180]. Thus the shift of the edge is a combined effect of plasma temperature and density.
The main challenge is the development of a suitable X-ray probe which has a smooth and wide spectral profile, the correct pulse duration, energy range and good shot-to-shot reproducibility. The first XANES experiments on WDM have mostly used broadband X-ray sources such as the M-band of transition between the
![]() $n=4$
and
$n=4$
and
![]() $n=3$
levels on various materials illuminated by optical lasers[Reference Dorchies105, Reference Lévy180]. An ultrafast measurement of the phase transition from crystalline solid to disordered liquid Al was observed using XANES spectroscopy by Dorchies et al.
[Reference Dorchies105]. Metallization of warm dense silica by a laser-driven shock to create conditions relevant to planetary interiors was observed using K-edge shift from the bottom of the valence band (insulator) down to the Fermi energy (semimetal) by Denoeud et al.
[Reference Denoeud181]. This experiment utilized XANES spectroscopic measurement at the Si K-edge using broadband X-ray source generated by a ps laser. This measurement was compared with EOS models used to determine the structural properties of both terrestrial and icy giant planets with abundance of complex silicates where the dissociation and metallization of SiO
$n=3$
levels on various materials illuminated by optical lasers[Reference Dorchies105, Reference Lévy180]. An ultrafast measurement of the phase transition from crystalline solid to disordered liquid Al was observed using XANES spectroscopy by Dorchies et al.
[Reference Dorchies105]. Metallization of warm dense silica by a laser-driven shock to create conditions relevant to planetary interiors was observed using K-edge shift from the bottom of the valence band (insulator) down to the Fermi energy (semimetal) by Denoeud et al.
[Reference Denoeud181]. This experiment utilized XANES spectroscopic measurement at the Si K-edge using broadband X-ray source generated by a ps laser. This measurement was compared with EOS models used to determine the structural properties of both terrestrial and icy giant planets with abundance of complex silicates where the dissociation and metallization of SiO
![]() $_{2}$
are of great interest. A similar experiment was carried out at the Advanced Light Source synchrotron by Engelhorn et al. on SiO
$_{2}$
are of great interest. A similar experiment was carried out at the Advanced Light Source synchrotron by Engelhorn et al. on SiO
![]() $_{2}$
isochorically heated by a short-pulse laser[Reference Engelhorn182].
$_{2}$
isochorically heated by a short-pulse laser[Reference Engelhorn182].

Figure 8. Temporally resolved measurement of X-ray absorption near K-edge (XANES) on 100 nm aluminium sample heated by a p-polarized 120 fs laser pulse at 800 nm, 6 J/cm
![]() $^{2}$
. Shots taken with different pump–probe relative delay show how the spectra change during the nonthermal melting of the sample transiting through the WDM regime. This data comes from an experiment by Dorchies et al. in Ref. [Reference Dorchies105].
$^{2}$
. Shots taken with different pump–probe relative delay show how the spectra change during the nonthermal melting of the sample transiting through the WDM regime. This data comes from an experiment by Dorchies et al. in Ref. [Reference Dorchies105].
The free electron laser X-ray beams have also been used to obtain XANES spectra. Even though these facilities deliver a narrow spectral range, tuneability or spectral jitter of these beams can be used to obtain spectral range broad enough for X-ray absorption spectroscopy. The first XANES measurement of Fe undergoing melt during shock compression at pressures reaching up to 420 GPa with strong relevance to material science and terrestrial as well as exoplanet structure and formation was obtained at an LCLS experiment by Harmand et al.
[Reference Harmand183]. Dorchies et al. carried out multiple experiments including temporally resolved observation of evolution of the electronic structure of warm dense Mo where a 300 fs 4 J/cm
![]() $^{2}$
laser beam was used to heat the samples and the X-ray probe was delivered by LCLS[Reference Dorchies184]. L-edge XANES measurements of the electronic structure in Cu heated by a short-pulse optical laser to warm dense regime were also carried out using the Advanced Light Source synchrotron by Cho et al.
[Reference Cho185].
$^{2}$
laser beam was used to heat the samples and the X-ray probe was delivered by LCLS[Reference Dorchies184]. L-edge XANES measurements of the electronic structure in Cu heated by a short-pulse optical laser to warm dense regime were also carried out using the Advanced Light Source synchrotron by Cho et al.
[Reference Cho185].
In the past years, novel laser-broadband betatron radiation sources based on laser-wakefield acceleration (LWFA) sources have been proposed as ideal probes for XANES spectroscopy on WDM[Reference Kneip186]. The main advantage of these sources is their high directionality (10 mrad beam divergence), short-pulse duration (30–40 fs), broad spectral range at high energy (up to
![]() ${\sim}10$
keV) and high brightness. While most of the current laser-driven betatrons operate at the 100 mJ to J energy level, novel PW level laser systems are now capable of generating bright enough X-ray beams for single shot absorption measurement on WDM. Such a source was used to obtain measurements of temporal evolution of ionization states in warm dense Al in the K-edge absorption[Reference Mo187]. These novel sources have also prompted development of new types of spectrometers capable of obtaining reference for the absorption spectra on every shot which is quite important to eliminate potential uncertainty due to shot-to-shot variation of the probe[Reference Mo188].
${\sim}10$
keV) and high brightness. While most of the current laser-driven betatrons operate at the 100 mJ to J energy level, novel PW level laser systems are now capable of generating bright enough X-ray beams for single shot absorption measurement on WDM. Such a source was used to obtain measurements of temporal evolution of ionization states in warm dense Al in the K-edge absorption[Reference Mo187]. These novel sources have also prompted development of new types of spectrometers capable of obtaining reference for the absorption spectra on every shot which is quite important to eliminate potential uncertainty due to shot-to-shot variation of the probe[Reference Mo188].
3.2.5 Emission spectroscopy
The use of emission spectroscopy for the study of WDM is rather limited mainly due to its high density and relatively low temperature, and thus the bulk of the material is mostly opaque to wavelengths of thermal emission. Self-emission from WDM is mainly in the optical or XUV regime and thus any observable radiation only comes from the surface of the material, as discussed above regarding the SOP diagnostic. It is however possible to use nonthermally excited emission from WDM to provide information on its thermodynamic properties in some special cases. For example if hot electrons are used to heat solids to WDM regime, the collisional ionization of the inner shell can generate K-
![]() $\unicode[STIX]{x03B1}$
emission. This emission originates from different ionization states depending on the temperature of the sample as shown by Hansen et al.
[Reference Hansen132]. In addition the Stark broadening of the lines in these degenerate high density states can be used to determine the thermodynamic state of WDM[Reference Hansen132]. Such measurements require high energy resolution spectrometers with
$\unicode[STIX]{x03B1}$
emission. This emission originates from different ionization states depending on the temperature of the sample as shown by Hansen et al.
[Reference Hansen132]. In addition the Stark broadening of the lines in these degenerate high density states can be used to determine the thermodynamic state of WDM[Reference Hansen132]. Such measurements require high energy resolution spectrometers with
![]() $E/\unicode[STIX]{x0394}E>2000$
. A similar experiment was carried out by Makita et al. where they measured temperature of solid Ti samples heated by laser-generated fast electrons to 20 eV from ionization spread in the K-
$E/\unicode[STIX]{x0394}E>2000$
. A similar experiment was carried out by Makita et al. where they measured temperature of solid Ti samples heated by laser-generated fast electrons to 20 eV from ionization spread in the K-
![]() $\unicode[STIX]{x03B1}$
emission spectrum[Reference Makita189].
$\unicode[STIX]{x03B1}$
emission spectrum[Reference Makita189].
Ciricosta et al. have carried out direct measurements of K-
![]() $\unicode[STIX]{x03B1}$
emission spectra from solid-density Al heated to WDM regime at 180 eV by the LCLS X-ray beam[Reference Ciricosta115]. They observed the K-
$\unicode[STIX]{x03B1}$
emission spectra from solid-density Al heated to WDM regime at 180 eV by the LCLS X-ray beam[Reference Ciricosta115]. They observed the K-
![]() $\unicode[STIX]{x03B1}$
fluorescence directly measuring the position of the K-edge of the highly ionized system. From these measurements they were able to directly compare different models for continuum lowering in warm dense Al with the shifts in the emission spectra finding significantly greater depression of the ionization potential than predicted by the widely accepted Stewart–Pyatt model, which is widely used in the modelling of planetary interiors[Reference Stewart and Pyatt176]. Hoarty et al. combined the technique of shock compression by long-pulse lasers to create high density states in Al targets and additional heating by electron beams accelerated by a short-pulse laser, which leads to strong emission of He-like Al ions. The effects of ionization potential depression was studied by Stark broadening of the emission lines from high density plasmas which in contrast to previous results by Ciricosta et al. found a closer agreement with the Stewart–Pyatt model[Reference Hoarty190].
$\unicode[STIX]{x03B1}$
fluorescence directly measuring the position of the K-edge of the highly ionized system. From these measurements they were able to directly compare different models for continuum lowering in warm dense Al with the shifts in the emission spectra finding significantly greater depression of the ionization potential than predicted by the widely accepted Stewart–Pyatt model, which is widely used in the modelling of planetary interiors[Reference Stewart and Pyatt176]. Hoarty et al. combined the technique of shock compression by long-pulse lasers to create high density states in Al targets and additional heating by electron beams accelerated by a short-pulse laser, which leads to strong emission of He-like Al ions. The effects of ionization potential depression was studied by Stark broadening of the emission lines from high density plasmas which in contrast to previous results by Ciricosta et al. found a closer agreement with the Stewart–Pyatt model[Reference Hoarty190].
3.2.6 Diffraction
X-ray diffraction is a traditional technique used to study structure of matter. It has been widely used to determine the crystalline structure and density of compressed materials usually carried out on statically compressed samples using DACs on synchrotron facilities. A classical example of X-ray diffraction studies of solid H at 26.5 GPa was carried out by Mao et al.
[Reference Mao95]. Recently, it has been demonstrated that in situ diffraction can also be used to obtain information about structure of transient states of matter opening a new pathway to study WDM and also reach more extreme conditions than those accessible by static compression. Implementing temporally resolved X-ray diffraction to dynamically compressed samples has been a true breakthrough for this field as it achieved the first direct measurement of microscopic structure and phase transitions during shock propagation. Nanosecond X-ray diffraction was used to observe the
![]() $\unicode[STIX]{x03B1}{-}\unicode[STIX]{x03F5}$
phase transition from the bcc to hcp crystalline structure in solid Fe compressed by a laser-driven shock[Reference Kalantar191]. Similar measurements were carried out on other metals including Cu[Reference Bringa192]. Advanced X-ray diffraction measurements combined with VISAR on solid Fe dynamically compressed by a laser-driven shock reaching pressures of 170 GPa and temperatures of 4150 K was obtained by Denoeud et al.
[Reference Denoeud193]. A ground-breaking experiment was carried out at the OMEGA laser facility by Coppari et al. utilizing X-ray diffraction and VISAR measurements of ramp-compressed magnesium oxide confirming the existence of a theoretically predicted solid–solid phase transition, consistent with a transformation to the B2 structure, which occurs near 600 GPa and remains stable to 900 GPa[Reference Coppari40]. This important result may help constrain mantle viscosity and convection in the deep mantle of extrasolar super-Earths. Other notable work was done by the same group using the experimental platform at the OMEGA laser on high pressure phases of iron, diamond and molybdenum at conditions of massive exoplanets[Reference Smith58, Reference Wang194, Reference Wang195].
$\unicode[STIX]{x03B1}{-}\unicode[STIX]{x03F5}$
phase transition from the bcc to hcp crystalline structure in solid Fe compressed by a laser-driven shock[Reference Kalantar191]. Similar measurements were carried out on other metals including Cu[Reference Bringa192]. Advanced X-ray diffraction measurements combined with VISAR on solid Fe dynamically compressed by a laser-driven shock reaching pressures of 170 GPa and temperatures of 4150 K was obtained by Denoeud et al.
[Reference Denoeud193]. A ground-breaking experiment was carried out at the OMEGA laser facility by Coppari et al. utilizing X-ray diffraction and VISAR measurements of ramp-compressed magnesium oxide confirming the existence of a theoretically predicted solid–solid phase transition, consistent with a transformation to the B2 structure, which occurs near 600 GPa and remains stable to 900 GPa[Reference Coppari40]. This important result may help constrain mantle viscosity and convection in the deep mantle of extrasolar super-Earths. Other notable work was done by the same group using the experimental platform at the OMEGA laser on high pressure phases of iron, diamond and molybdenum at conditions of massive exoplanets[Reference Smith58, Reference Wang194, Reference Wang195].
A true revolution for diffraction studies of phase transitions and dynamic structural changes in WDM came with the birth of free electron laser facilities capable of providing coherent beams of X-rays with femtosecond pulse duration at high energies. Especially in combination with high energy lasers capable of simultaneously compressing and heating samples to WDM conditions, these become very powerful tools to study ultrafast structural changes of matter. The new MEC station at the LCLS facility, which specializes in extreme states of matter and provides an unique combination of laser systems with the X-ray FEL beam, hosted an experiment by Gorman et al., who were studying the poorly understood melting line of bismuth. The shock-compressed samples were probed with femtosecond X-ray diffraction combined with VISAR[Reference Gorman196]. Changes in the observed diffraction patterns were used to monitor phase transitions within the Bi upon release. More recently ultrafast X-ray diffraction capability at LCLS was utilized by Briggs et al. to study phase transitions and EOS of scandium shock-compressed to 82 GPa[Reference Briggs197].
Gleason et al. also used the LCLS capabilities to carry out a remarkable study of high pressure phases of dynamically compressed SiO
![]() $_{2}$
[Reference Gleason45, Reference Gleason198]. They observed shock-induced crystallization of an amorphous material and rapid growth of nanocrystalline stishovite grains with strong relevance to geophysics, understanding of physical processes during collisions of celestial bodies, and fundamental shock physics. In the most recent experiments, they observed real-time diaplectic glass formation indicating that it is a back-transformation product of stishovite with implications for revising traditional shock metamorphism stages during asteroid impacts. This group also experimentally verified the freezing of water to ice VII[Reference Gleason36]. In this LCLS experiment a laser was used to drive a planar shock in diamond–water–quartz sandwich targets, which was diagnosed with a combination of femtosecond X-ray diffraction with VISAR. This experiment demonstrated crystallization rather than amorphous solidification during compression freezing, which has serious implications for modelling of ice phases present in icy moons and extrasolar planetary bodies, and evaluation of extreme condition behaviour of impurity-laden ices in planetary interiors.
$_{2}$
[Reference Gleason45, Reference Gleason198]. They observed shock-induced crystallization of an amorphous material and rapid growth of nanocrystalline stishovite grains with strong relevance to geophysics, understanding of physical processes during collisions of celestial bodies, and fundamental shock physics. In the most recent experiments, they observed real-time diaplectic glass formation indicating that it is a back-transformation product of stishovite with implications for revising traditional shock metamorphism stages during asteroid impacts. This group also experimentally verified the freezing of water to ice VII[Reference Gleason36]. In this LCLS experiment a laser was used to drive a planar shock in diamond–water–quartz sandwich targets, which was diagnosed with a combination of femtosecond X-ray diffraction with VISAR. This experiment demonstrated crystallization rather than amorphous solidification during compression freezing, which has serious implications for modelling of ice phases present in icy moons and extrasolar planetary bodies, and evaluation of extreme condition behaviour of impurity-laden ices in planetary interiors.

Figure 9. A schematic of a X-ray diffraction setup at the Matter at Extreme Conditions (MEC) end-station of the LCLS. A double shock is driven inside a polystyrene sample by a stepped laser drive created by overlapping two laser pulses. The shock conditions are recorded by a line-imaging VISAR diagnostic and the microscopic structure of extreme carbon states are measured using single X-ray pulses with 8.2 keV energy and 50 fs pulse duration recorded by a large area X-ray detector. Diamond signature is detected during the second shock formation[Reference Kraus35].
The shock-induced transition from graphite to diamond at ns time scales under conditions of planetary interiors was observed using in situ X-ray diffraction at the LCLS facility by Kraus et al.
[Reference Kraus46]. Two optical lasers, with 16 J energy and 10 ns pulse duration each, were used to ablatively drive a strong shock in pyrolitic and polycrystalline graphite samples to 228 GPa. The LCLS X-ray beam with 50 fs pulse duration was used as a probe for the dynamic diffraction diagnostic. This data was complemented by a line-imaging VISAR for shock transit measurements. The transition to diamond was found to start at 50 GPa for both types of graphite. A shock-induced phase transition to lonsdaleite was found at 170 GPa for pyrolitic graphite only[Reference Kraus46]. These findings provide new insights into the high pressure phases of carbon both for planetary interiors as well as asteroid impacts on terrestrial bodies and planetary formation explaining why the main natural occurrence of lonsdaleite crystal structures is in close proximity of meteor impact sites. Kraus et al. continued their experiments at LCLS and demonstrated the transition of polystyrene (C
![]() $_{8}$
H
$_{8}$
H
![]() $_{8}$
) to diamond by X-ray diffraction of dynamically compressed samples to WDM conditions at 150 GPa and 5000 K (
$_{8}$
) to diamond by X-ray diffraction of dynamically compressed samples to WDM conditions at 150 GPa and 5000 K (
![]() ${\sim}0.4$
eV)[Reference Kraus35]. A typical setup and diffraction images for these experiments are shown in Figure 9. This experiment is the first experimental confirmation of phase transitions predicted for simple hydrocarbons, which under the extreme conditions of deep planetary layers undergo separation into hydrogen and diamond leading to diamond precipitation in the atmospheres of icy giants[Reference Ross32].
${\sim}0.4$
eV)[Reference Kraus35]. A typical setup and diffraction images for these experiments are shown in Figure 9. This experiment is the first experimental confirmation of phase transitions predicted for simple hydrocarbons, which under the extreme conditions of deep planetary layers undergo separation into hydrogen and diamond leading to diamond precipitation in the atmospheres of icy giants[Reference Ross32].
Ultrafast electron diffraction is also becoming a viable option for the study of dynamic structure changes in systems under extreme pressures and temperatures. Structural evolution of polycrystalline Al at solid–liquid phase transition with 600 fs temporal resolution was investigated using pump-and-probe experiments with short-pulse lasers[Reference Siwick199]. Ground-breaking work by Ernstorfer et al. provided the first experimental evidence of electronic bond-hardening in warm dense gold with femtosecond electron diffraction[Reference Ernstorfer200]. In this experiment nonthermal melt to dense plasma state in thin gold films was induced by a short-pulse laser synchronized with an ultrafast electron beam capable of probing transient states on nonequilibrium time scales. Novel LWFA electron sources in the downramp density gradient regime achieving electron beams at lower energies (below 1 MeV) suitable for diffraction in solids and WDM have recently been demonstrated[Reference He201]. He et al. have been able to use such laser-driven electron beams to study dynamic changes in Si lattice pumped by an optical laser with picosecond temporal resolution[Reference He201]. Their results suggest that hundreds of or even tens of femtosecond temporal resolution could be possible with such a system.
3.2.7 Phase contrast imaging
The X-ray phase contrast imaging (PCI) is a relatively new diagnostic to be used to study WDM and other high energy density systems. It was recently applied to laser-driven shock experiments and characterization of fusion capsules for ICF applications[Reference Workman202–Reference Montgomery204]. While dense plasmas are nominally transparent to traditional X-ray absorption, the PCI diagnostic relies on gradients in the refractive index and wave interference, to characterize density fluctuations in studied samples. PCI is simply an interference phenomenon due to gradients in the phase induced by density fluctuations in, e.g., a moving solid-density shock front or ICF fuel pellet. Combined with an imaging system, PCI can provide accurate information on both density and structure of dense objects with well-matched density gradients to the X-ray probe parameters. The advantage of PCI is that fairly broad spectral sources (up to
![]() $\unicode[STIX]{x0394}\unicode[STIX]{x1D706}/\unicode[STIX]{x1D706}\sim 1$
) may be used without a severe loss of contrast. However, stringent requirements for spatial coherence need to be met in order to observe phase contrast effects putting some restrictions on the geometry of the experiment and source parameters. A clear description of PCI is provided in a publication by Montgomery et al.
[Reference Montgomery204]. High energy X-rays (
$\unicode[STIX]{x0394}\unicode[STIX]{x1D706}/\unicode[STIX]{x1D706}\sim 1$
) may be used without a severe loss of contrast. However, stringent requirements for spatial coherence need to be met in order to observe phase contrast effects putting some restrictions on the geometry of the experiment and source parameters. A clear description of PCI is provided in a publication by Montgomery et al.
[Reference Montgomery204]. High energy X-rays (
![]() ${>}10$
keV) can be efficiently produced from ultrafast laser target interactions as described in previous sections[Reference Workman202]. These X-rays can also be applied to measurements of low density materials inside high density hohlraum environments in ICF research[Reference Workman202].
${>}10$
keV) can be efficiently produced from ultrafast laser target interactions as described in previous sections[Reference Workman202]. These X-rays can also be applied to measurements of low density materials inside high density hohlraum environments in ICF research[Reference Workman202].
Pioneering work on X-ray phase contrast imaging of laser-driven shocks in polystyrene was carried out by Workman et al. at the TRIDENT laser facility in Los Alamos, utilizing their unique combination of long- and short-pulse lasers[Reference Workman202]. Planar shocks were driven in the targets using 250 J of 532 nm laser light with 2 ns square temporal profile, while the X-ray backlighter was created on molybdenum wires irradiated by a short-pulse laser with intensity of
![]() $2\times 10^{19}~\text{W/cm}^{2}$
and pulse duration
$2\times 10^{19}~\text{W/cm}^{2}$
and pulse duration
![]() ${\sim}600$
fs. Alternatively synchrotrons have been used as an X-ray source for PCI on dynamic compression of dense plasma targets. A novel compact gas-gun system was used to drive a strong shock in an experiment by Luo et al. at the Advanced Photon Source[Reference Luo85]. Single-pulse PCI was employed in combination with X-ray diffraction to study microstructure effects on dynamic material response.
${\sim}600$
fs. Alternatively synchrotrons have been used as an X-ray source for PCI on dynamic compression of dense plasma targets. A novel compact gas-gun system was used to drive a strong shock in an experiment by Luo et al. at the Advanced Photon Source[Reference Luo85]. Single-pulse PCI was employed in combination with X-ray diffraction to study microstructure effects on dynamic material response.
PCI has now shown a great new potential for time-resolved studies of laser-driven shock experiments at X-ray free electron facilities. The first dedicated instrument for PCI has now been deployed at LCLS[Reference Nagler205]. The first in situ X-ray PCI with both high temporal and spatial resolution on laser-driven shocks in diamond was developed by Schropp et al. at the MEC station at LCLS[Reference Schropp206]. Similar experiments were carried out by Hawreliak et al. [Reference Hawreliak207] on low density silica aerogel, which is a standard low density material used in shock physics experiments and ICF to achieve very high temperature and pressure states. Such measurements provide detailed information on shock dynamics, such as the shock velocity, the shock front width and the local compression of the material with a quantitative perspective on the state of matter under extreme conditions.
4 Theoretical models
Hydrogen is the main constituent element of all large planets and brown dwarfs and is also important for ICF, and thus much attention has been dedicated to the study of hydrogen phase diagram and EOS. One of the most widely used EOS models for various elements is the SESAME table. The first SESAME model for hydrogen and deuterium was computed by Kerley primarily for ICF applications[Reference Kerley208]. Another important EOS model for hydrogen was computed by Saumon and Chabrier (S&C)[Reference Saumon and Chabrier209, Reference Saumon and Chabrier210]. It spans a wide range of conditions and is mostly used for astrophysical purposes. SESAME and S&C are both based on a chemical model. While S&C is purely theoretical, SESAME includes many adjustments based on experiments. This EOS considers three ideal phases (fluid, molecular solid and metallic solid) and includes dissociation, ionization and linear mixing of the combined molecular and atomic fluid phases. This EOS however underestimates the effects of strong coupling and quantum degeneracy in the nonideal plasma[Reference Hu211]. In the case of astrophysical S&C model, a free energy minimization method is used to determine the concentrations of atoms, molecules, protons and electrons, and a two-fluid model is used at high densities. Effective pair potentials are used to model the interactions between hydrogen atoms and molecules. The main disadvantage of these chemical models is the fact that they do not treat the quantum and correlation effects between individual particles explicitly, which leads to large errors in the WDM regime.
Novel ab initio methods such as the quantum molecular dynamics (QMD), where a sophisticated quantal treatment is employed for the electrons, combined with a molecular dynamics solution for the classical equations of motion for the ions. The quantum mechanical treatment of the electron species is often based on density-functional theory (DFT) and such DFT-MD simulations where electrons and ions handled as elementary particles allow a more realistic physical picture[Reference Vorberger13, Reference Vorberger14, Reference Grinenko212]. Properties of the electrons are calculated using a Mermin functional that accounts for temperature effects within the electron subsystem in a statistical sense. The dynamics of ions and electrons is effectively decoupled with the Born–Oppenheimer approximation. This description of hydrogen avoids most approximations concerning the composition and mixing[Reference Vorberger13]. Other QMD simulations are also available[Reference Recoules213]. QMD has been successfully applied to describe the properties of warm dense carbon and hydrocarbons such as the EOS for shock-compressed methane (CH
![]() $_{4}$
)[Reference Kress, Bickham and Collins214], benzene (C
$_{4}$
)[Reference Kress, Bickham and Collins214], benzene (C
![]() $_{6}$
H
$_{6}$
H
![]() $_{6}$
)[Reference Bickham, Kress and Collins215], polymers[Reference Mattsson, Lane, Cochrane, Desjarlais, Thompson, Pierce and Grest216] and diamond[Reference Knudson, Desjarlais and Dolan217, Reference Driver and Militzer218] and for the EOS and electrical conductivity of shock-compressed ICF ablators containing plastic[Reference Hanson, Collins and Desjarlais219, Reference Lambert and Recoules220]. The limitation with many models such as QMD is that they are restricted to a smaller area of the phase diagram, i.e., they are confined to moderately low temperatures of several eV. Another method, quantum Monte Carlo, is applicable at higher temperatures but can only be used for very low
$_{6}$
)[Reference Bickham, Kress and Collins215], polymers[Reference Mattsson, Lane, Cochrane, Desjarlais, Thompson, Pierce and Grest216] and diamond[Reference Knudson, Desjarlais and Dolan217, Reference Driver and Militzer218] and for the EOS and electrical conductivity of shock-compressed ICF ablators containing plastic[Reference Hanson, Collins and Desjarlais219, Reference Lambert and Recoules220]. The limitation with many models such as QMD is that they are restricted to a smaller area of the phase diagram, i.e., they are confined to moderately low temperatures of several eV. Another method, quantum Monte Carlo, is applicable at higher temperatures but can only be used for very low
![]() $Z$
materials such as H and He[Reference Militzer221]. There are other theoretical models that have a wider range of applicability such as classical or quantum hypernetted-chain (HNC) methods[Reference Saumon222] and other orbital free density-functional methods[Reference Ofer, Nardi and Rosenfeld223], but comparisons of these models to data in the WDM region have been very limited so far.
$Z$
materials such as H and He[Reference Militzer221]. There are other theoretical models that have a wider range of applicability such as classical or quantum hypernetted-chain (HNC) methods[Reference Saumon222] and other orbital free density-functional methods[Reference Ofer, Nardi and Rosenfeld223], but comparisons of these models to data in the WDM region have been very limited so far.
Both ab initio and the SESAME EOS assume lower compressibility of hydrogen at high pressure than S&C. The EOS of light elements in the WDM regime is crucial to the internal structure of planets. As shown by Nettelmann et al. the use of different EOS models creates completely different structures of the internal structure of Jupiter, yet they all reproduce the same gravitational moments and agree with observation by inter-planetary probes[Reference Nettelmann10]. Saumon and Guillot have shown that the interior structure of Jupiter is surprisingly sensitive to the details concerning the hydrogen EOS at high pressures[Reference Saumon and Guillot224].
The properties of water at high pressures and temperatures elevated to the WDM regime conditions are very important for understanding of the interiors of icy giants. The pressure H
![]() $_{2}$
O phase diagram still suffers from large uncertainties. Several different phases have been predicted theoretically[Reference Cavazzoni225]. A transition to a superionic solid is predicted at
$_{2}$
O phase diagram still suffers from large uncertainties. Several different phases have been predicted theoretically[Reference Cavazzoni225]. A transition to a superionic solid is predicted at
![]() $P>100$
GPa and
$P>100$
GPa and
![]() $T>2000$
K (
$T>2000$
K (
![]() ${\sim}0.2$
eV) with body-centred-cubic (bcc) lattice structure of oxygen atoms and free protons. At such conditions water is an ionic conductor but electronic insulator. At temperatures exceeding 3500 K (
${\sim}0.2$
eV) with body-centred-cubic (bcc) lattice structure of oxygen atoms and free protons. At such conditions water is an ionic conductor but electronic insulator. At temperatures exceeding 3500 K (
![]() ${\sim}0.3$
eV) the oxygen lattice melts into a two-component ionic liquid, which is still an electronic insulator and ionic conductor. The transition to a metal fluid occurs at 7000–7500 K (
${\sim}0.3$
eV) the oxygen lattice melts into a two-component ionic liquid, which is still an electronic insulator and ionic conductor. The transition to a metal fluid occurs at 7000–7500 K (
![]() ${\sim}0.6$
–0.64 eV) when the electronic band gap closes.
${\sim}0.6$
–0.64 eV) when the electronic band gap closes.
Significant progress has been made recently in the theoretical description of transport properties of WDM with novel approaches to compute EOS and microscopic structure[Reference Driver and Militzer218, Reference Saumon222]. Examples of remarkable work include ab initio quantum molecular dynamics (QMD) simulations obtaining thermal conductivity of warm dense hydrogen[Reference Recoules213], resistivity saturation in warm dense Al[Reference Faussurier and Blancard226] and charged particle stopping powers and transport has been described both by using pure theory as well as with MD simulations[Reference Li and Petrasso227, Reference Grabowski228]. The Cimarron project provided a computational tool for simulating electron–ion coupling and charged particle transport with further capabilities to evaluate thermal conductivity, diffusivity and EOS in dense plasmas[Reference Graziani229]. Effective potential theory (EPT) for transport coefficients for both weakly and strongly coupled systems has been developed and compared with MD simulations[Reference Baalrud and Daligault230]. It was then being utilized in a newly developed theory for thermal diffusion in multiple ion species relevant to ICF conditions[Reference Kagan and Tang231].
For an interested reader, a more comprehensive overview of the theoretical description of WDM is provided by Granziani in Ref. [Reference Ganziani2].
5 Summary
During the past two decades the research of WDM has experienced an accelerated development thanks to the availability of novel high power laser and accelerator facilities. This field gained a lot of interest among scientists from various fields including astrophysics, geophysics, material science, shock physics and energy. WDM is particularly dominant inside large gaseous, but also rocky planets, ice giants, brown dwarfs or crusts of old stars. It also appears in many dynamic processes like collisions of celestial bodies and astrophysical shock waves. The knowledge of WDM structure and transport properties is of utmost importance for understanding of magnetic dynamos, layer structure, convection and formation of these astrophysical objects. WDM also plays an important role in the study of ICF implosions, as it is one of the transient states the DT fuel pellets must go through prior to ignition, and is of interest to high pressure and shock physics including relation to the development of explosives. It is a very challenging regime of matter to describe theoretically due to strong correlation and quantum effects that influence the structure and equation of state, which does not allow for many of the standard approximations used in computational or analytical models. Thus, the experimental verification of these models is very important. However, WDM is also rather difficult to generate in a controlled manner and to diagnose. The standard experimental methods to both create and study WDM have been described in detail.
The new high power laser and accelerator facilities have provided new approaches to produce heated dense matter states under controlled conditions. Several techniques to generate WDM have been described in this paper. The most traditional one makes use of diamond anvil cells to statically compress matter samples to very high pressures, which then can be heated to WDM states with a laser. The primary limitation of DAC is that it can only reach relatively low temperatures and thus cannot access all of the relevant conditions. Another very common way to produce WDM is by driving a strong shock wave in solid or liquid targets with high power lasers, z-pinches or gas guns. The dynamic compression approach with single shocks produces dense states on the principal Hugoniot. Multiple shocks, shock-and-release or ramp compression techniques can then be used to generate off-Hugoniot states. A combination of pre-compressed targets with DAC then further compressed and heated by a shock wave driven by a laser has been used to achieve even more extreme pressures and temperatures. Isochoric heating with X-rays or protons has also been demonstrated on solid samples to produce solid-density heated states different from those lying on the principal Hugoniot under short-time scales prior to the hydrodynamic expansion. Short-pulse optical lasers and X-ray free electron lasers with femtosecond duration pulses now provide a unique opportunity to access nonequilibrium dynamics in WDM.
WDM is a highly challenging regime to study with traditional plasma diagnostic methods which usually employ optical probes such as lasers or rely on self-emission for spectroscopic measurements. Due to high density and relatively low temperatures of WDM none of these diagnostics can be used as optical emission that cannot penetrate such high densities and WDM is not hot enough for sufficient X-ray emission in most cases. Optical diagnostics like VISAR or SOP as well as emission spectroscopy have been used to study the thermodynamic state of WDM, but are limited to surface measurements. That is why X-ray Thomson scattering was such a revolution for the field since this diagnostic provided a way to use external narrow-band X-ray sources, usually driven by lasers, to directly measure the full thermodynamic state including temperature, density, ionization state and the microscopic structure of bulk material under a wide range of conditions. This diagnostic has also been extended to the short-time scales thanks to new optical and X-ray lasers with femtosecond pulse duration. Additional methods including X-ray radiography, absorption spectroscopy or diffraction has been used to directly probe WDM and obtain measurements of its thermodynamics and structure. Specifically ultrafast X-ray diffraction capable of providing in situ measurements of structure and phase transitions in dynamically compressed material has been an enormous leap forward for this whole field. Since each diagnostic has some limitation and often relies on some modelling to extract more complete information about the WDM sample, the most reliable experiments have used a combination of different methods to obtain full EOS measurements without the support of theoretical calculations. These usually combine XRTS or X-ray diffraction with VISAR, SOP and radiography.
Better understanding of structure and transport properties for different elements, mixtures or compounds under WDM conditions has been achieved thanks to many experimental efforts and has now shed light on the composition and evolution of many astrophysical objects and phenomena. The phase separation of elements including H, He and C at conditions of gas giant interiors has been studied both theoretically and experimentally confirming the possibility of the presence of helium and diamond precipitation in the envelopes of large planets. Metallic hydrogen and carbon in the warm dense regime that is relevant to planetary dynamo formation have been confirmed to exist during experiments at high power laser facilities. High pressure phases of iron have been confirmed in dynamic compression experiments. Significant progress was made in the study of high pressure phases and behaviour of composite materials such as complex silicates or MgO that can be found in small rocky planets, asteroids or extrasolar super-Earths. New phases of these materials have been experimentally confirmed and transitions to conductive metallic state were found, which has a very significant impact on the modelling of magnetic field generation inside celestial bodies. High pressure phases of water and other materials common in ice giants, comets or icy asteroids have also been explored with novel experimental methods. Numerous experiments focused on the study of thermodynamic conditions of WDM have led to significant improvement of theoretical models for equation of state and planetary structure and evolution. With improved laser and diagnostic technologies, especially short-pulse facilities as well as computer power significant progress is still expected for the future with the promise to answer many more big questions in planetary science, geophysics or high pressure material properties.
Acknowledgements
The author would like to thank P. Davis, S. H. Glenzer, F. Dorchies, D. Kraus and D. Jung for providing original figures with results from their experiments. Special thanks also go to D. Riley for providing valuable guidance. K. Falk is supported by the Helmholtz Association under VH-NG-1338.